Fine-Grained Urban Traffic Forecasting on Metropolis-Scale Road Networks

Traffic forecasting on road networks is a complex task of significant practical importance that has recently attracted considerable attention from the machine learning community, with spatiotemporal graph neural networks (GNNs) becoming the most popular approach. The proper evaluation of traffic forecasting methods requires realistic datasets, but current publicly available benchmarks have significant drawbacks, including the absence of information about road connectivity for road graph construction, limited information about road properties, and a relatively small number of road segments that falls short of real-world applications. Further, current datasets mostly contain information about intercity highways with sparsely located sensors, while city road networks arguably present a more challenging forecasting task due to much denser roads and more complex urban traffic patterns. In this work, we provide a more complete, realistic, and challenging benchmark for traffic forecasting by releasing datasets representing the road networks of two major cities, with the largest containing almost 100,000 road segments (more than a 10-fold increase relative to existing datasets). Our datasets contain rich road features and provide fine-grained data about both traffic volume and traffic speed, allowing for building more holistic traffic forecasting systems. We show that most current implementations of neural spatiotemporal models for traffic forecasting have problems scaling to datasets of our size. To overcome this issue, we propose an alternative approach to neural traffic forecasting that uses a GNN without a dedicated module for temporal sequence processing, thus achieving much better scalability, while also demonstrating stronger forecasting performance. We hope our datasets and modeling insights will serve as a valuable resource for research in traffic forecasting.

Turning Tabular Foundation Models into Graph Foundation Models

While foundation models have revolutionized such fields as natural language processing and computer vision, their application and potential within graph machine learning remain largely unexplored. One of the key challenges in designing graph foundation models (GFMs) is handling diverse node features that can vary across different graph datasets. Although many works on GFMs have been focused exclusively on text-attributed graphs, the problem of handling arbitrary features of other types in GFMs has not been fully addressed. However, this problem is not unique to the graph domain, as it also arises in the field of machine learning for tabular data. In this work, motivated by the recent success of tabular foundation models like TabPFNv2, we propose G2T-FM, a simple graph foundation model that employs TabPFNv2 as a backbone. Specifically, G2T-FM augments the original node features with neighborhood feature aggregation, adds structural embeddings, and then applies TabPFNv2 to the constructed node representations. Even in a fully in-context regime, our model achieves strong results, significantly outperforming publicly available GFMs and performing on par with well-tuned GNNs trained from scratch. Moreover, after finetuning, G2T-FM surpasses well-tuned GNN baselines, highlighting the potential of the proposed approach. More broadly, our paper reveals a previously overlooked direction of utilizing tabular foundation models for graph machine learning tasks.

Revisiting Graph Homophily Measures

Homophily is a graph property describing the tendency of edges to connect similar nodes. There are several measures used for assessing homophily but all are known to have certain drawbacks: in particular, they cannot be reliably used for comparing datasets with varying numbers of classes and class size balance. To show this, previous works on graph homophily suggested several properties desirable for a good homophily measure, also noting that no existing homophily measure has all these properties. Our paper addresses this issue by introducing a new homophily measure - unbiased homophily - that has all the desirable properties and thus can be reliably used across datasets with different label distributions. The proposed measure is suitable for undirected (and possibly weighted) graphs. We show both theoretically and via empirical examples that the existing homophily measures have serious drawbacks while unbiased homophily has a desirable behavior for the considered scenarios. Finally, when it comes to directed graphs, we prove that some desirable properties contradict each other and thus a measure satisfying all of them cannot exist.

Measuring Diversity: Axioms and Challenges

The concept of diversity is widely used in various applications: from image or molecule generation to recommender systems. Thus, being able to properly measure diversity is important. This paper addresses the problem of quantifying diversity for a set of objects. First, we make a systematic review of existing diversity measures and explore their undesirable behavior in some cases. Based on this review, we formulate three desirable properties (axioms) of a reliable diversity measure: monotonicity, uniqueness, and continuity. We show that none of the existing measures has all three properties and thus these measures are not suitable for quantifying diversity. Then, we construct two examples of measures that have all the desirable properties, thus proving that the list of axioms is not self-contradicting. Unfortunately, the constructed examples are too computationally complex for practical use, thus we pose an open problem of constructing a diversity measure that has all the listed properties and can be computed in practice.

Challenges of Generating Structurally Diverse Graphs

For many graph-related problems, it can be essential to have a set of structurally diverse graphs. For instance, such graphs can be used for testing graph algorithms or their neural approximations. However, to the best of our knowledge, the problem of generating structurally diverse graphs has not been explored in the literature. In this paper, we fill this gap. First, we discuss how to define diversity for a set of graphs, why this task is non-trivial, and how one can choose a proper diversity measure. Then, for a given diversity measure, we propose and compare several algorithms optimizing it: we consider approaches based on standard random graph models, local graph optimization, genetic algorithms, and neural generative models. We show that it is possible to significantly improve diversity over basic random graph generators. Additionally, our analysis of generated graphs allows us to better understand the properties of graph distances: depending on which diversity measure is used for optimization, the obtained graphs may possess very different structural properties which gives insights about the sensitivity of the graph distance underlying the diversity measure.

TabGraphs: A Benchmark and Strong Baselines for Learning on Graphs with Tabular Node Features

Tabular machine learning is an important field for industry and science. In this field, table rows are usually treated as independent data samples, but additional information about relations between them is sometimes available and can be used to improve predictive performance. Such information can be naturally modeled with a graph, thus tabular machine learning may benefit from graph machine learning methods. However, graph machine learning models are typically evaluated on datasets with homogeneous node features, which have little in common with heterogeneous mixtures of numerical and categorical features present in tabular datasets. Thus, there is a critical difference between the data used in tabular and graph machine learning studies, which does not allow one to understand how successfully graph models can be transferred to tabular data. To bridge this gap, we propose a new benchmark of diverse graphs with heterogeneous tabular node features and realistic prediction tasks. We use this benchmark to evaluate a vast set of models, including simple methods previously overlooked in the literature. Our experiments show that graph neural networks (GNNs) can indeed often bring gains in predictive performance for tabular data, but standard tabular models also can be adapted to work with graph data by using simple feature preprocessing, which sometimes enables them to compete with and even outperform GNNs. Based on our empirical study, we provide insights for researchers and practitioners in both tabular and graph machine learning fields.

Discrete Neural Algorithmic Reasoning

Neural algorithmic reasoning aims to capture computations with neural networks via learning the models to imitate the execution of classical algorithms. While common architectures are expressive enough to contain the correct model in the weights space, current neural reasoners are struggling to generalize well on out-of-distribution data. On the other hand, classical computations are not affected by distribution shifts as they can be described as transitions between discrete computational states. In this work, we propose to force neural reasoners to maintain the execution trajectory as a combination of finite predefined states. Trained with supervision on the algorithm's state transitions, such models are able to perfectly align with the original algorithm. To show this, we evaluate our approach on the SALSA-CLRS benchmark, where we get perfect test scores for all tasks. Moreover, the proposed architectural choice allows us to prove the correctness of the learned algorithms for any test data.

Neural Algorithmic Reasoning Without Intermediate Supervision

Neural Algorithmic Reasoning is an emerging area of machine learning focusing on building models which can imitate the execution of classic algorithms, such as sorting, shortest paths, etc. One of the main challenges is to learn algorithms that are able to generalize to out-of-distribution data, in particular with significantly larger input sizes. Recent work on this problem has demonstrated the advantages of learning algorithms step-by-step, giving models access to all intermediate steps of the original algorithm. In this work, we instead focus on learning neural algorithmic reasoning only from the input-output pairs without appealing to the intermediate supervision. We propose simple but effective architectural improvements and also build a self-supervised objective that can regularise intermediate computations of the model without access to the algorithm trajectory. We demonstrate that our approach is competitive to its trajectory-supervised counterpart on tasks from the CLRS Algorithmic Reasoning Benchmark and achieves new state-of-the-art results for several problems, including sorting, where we obtain significant improvements. Thus, learning without intermediate supervision is a promising direction for further research on neural reasoners.

Evaluating Robustness and Uncertainty of Graph Models Under Structural Distributional Shifts

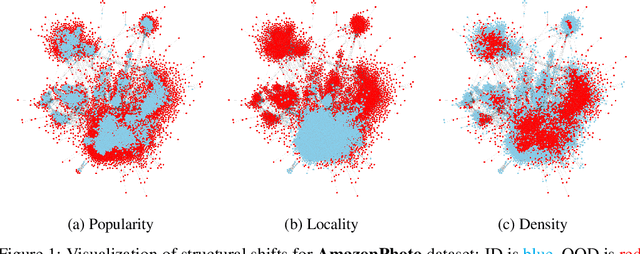
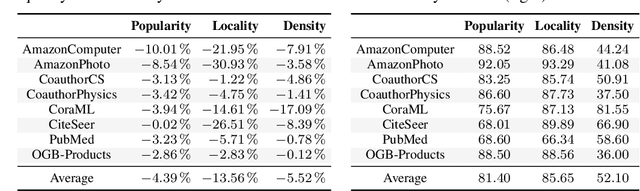
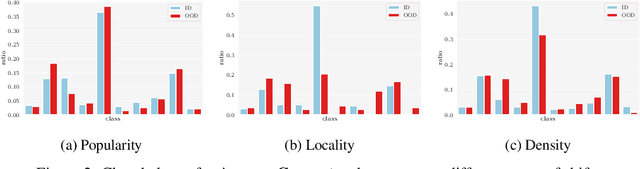
In reliable decision-making systems based on machine learning, models have to be robust to distributional shifts or provide the uncertainty of their predictions. In node-level problems of graph learning, distributional shifts can be especially complex since the samples are interdependent. To evaluate the performance of graph models, it is important to test them on diverse and meaningful distributional shifts. However, most graph benchmarks that consider distributional shifts for node-level problems focus mainly on node features, while data in graph problems is primarily defined by its structural properties. In this work, we propose a general approach for inducing diverse distributional shifts based on graph structure. We use this approach to create data splits according to several structural node properties: popularity, locality, and density. In our experiments, we thoroughly evaluate the proposed distributional shifts and show that they are quite challenging for existing graph models. We hope that the proposed approach will be helpful for the further development of reliable graph machine learning.

A critical look at the evaluation of GNNs under heterophily: are we really making progress?

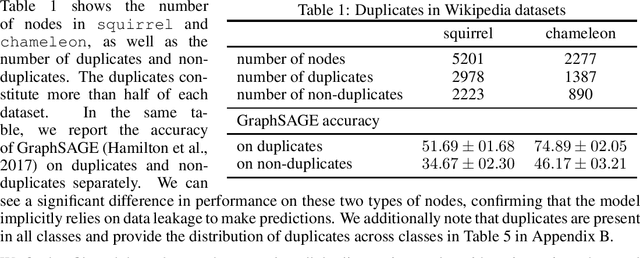
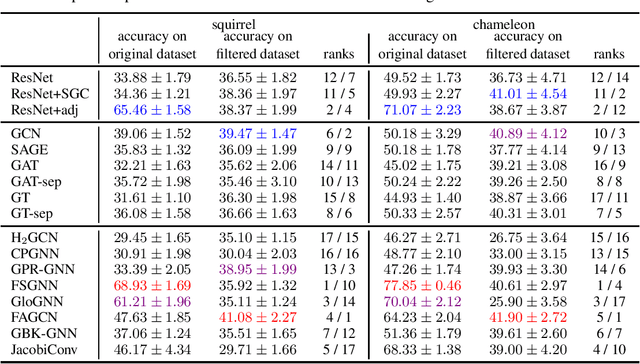
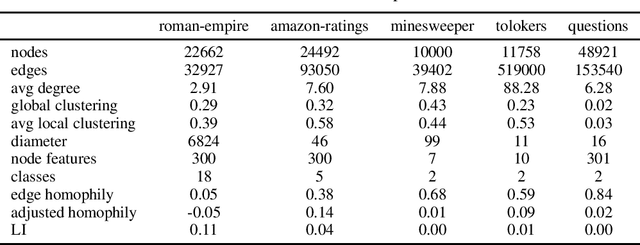
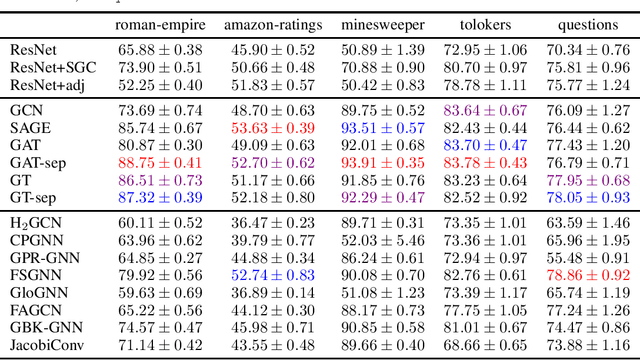
Node classification is a classical graph representation learning task on which Graph Neural Networks (GNNs) have recently achieved strong results. However, it is often believed that standard GNNs only work well for homophilous graphs, i.e., graphs where edges tend to connect nodes of the same class. Graphs without this property are called heterophilous, and it is typically assumed that specialized methods are required to achieve strong performance on such graphs. In this work, we challenge this assumption. First, we show that the standard datasets used for evaluating heterophily-specific models have serious drawbacks, making results obtained by using them unreliable. The most significant of these drawbacks is the presence of a large number of duplicate nodes in the datsets Squirrel and Chameleon, which leads to train-test data leakage. We show that removing duplicate nodes strongly affects GNN performance on these datasets. Then, we propose a set of heterophilous graphs of varying properties that we believe can serve as a better benchmark for evaluating the performance of GNNs under heterophily. We show that standard GNNs achieve strong results on these heterophilous graphs, almost always outperforming specialized models. Our datasets and the code for reproducing our experiments are available at https://github.com/yandex-research/heterophilous-graphs