Characterizing Graph Datasets for Node Classification: Beyond Homophily-Heterophily Dichotomy

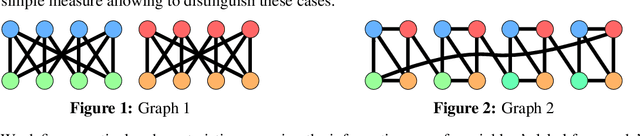
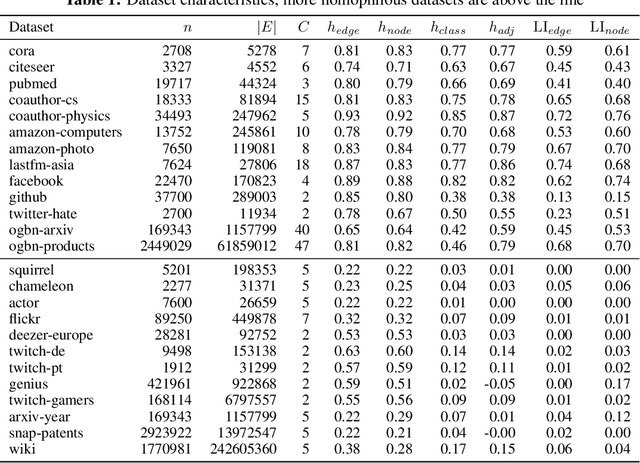
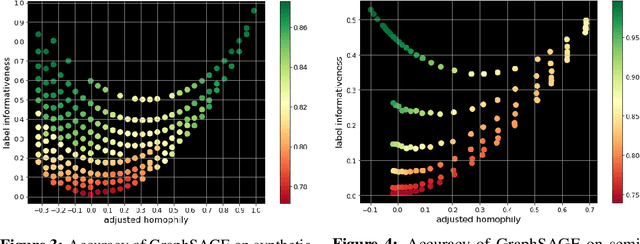
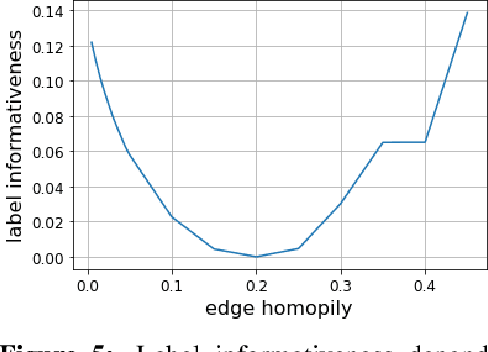
Homophily is a graph property describing the tendency of edges to connect similar nodes; the opposite is called heterophily. While homophily is natural for many real-world networks, there are also networks without this property. It is often believed that standard message-passing graph neural networks (GNNs) do not perform well on non-homophilous graphs, and thus such datasets need special attention. While a lot of effort has been put into developing graph representation learning methods for heterophilous graphs, there is no universally agreed upon measure of homophily. Several metrics for measuring homophily have been used in the literature, however, we show that all of them have critical drawbacks preventing comparison of homophily levels between different datasets. We formalize desirable properties for a proper homophily measure and show how existing literature on the properties of classification performance metrics can be linked to our problem. In doing so we find a measure that we call adjusted homophily that satisfies more desirable properties than existing homophily measures. Interestingly, this measure is related to two classification performance metrics - Cohen's Kappa and Matthews correlation coefficient. Then, we go beyond the homophily-heterophily dichotomy and propose a new property that we call label informativeness (LI) that characterizes how much information a neighbor's label provides about a node's label. We theoretically show that LI is comparable across datasets with different numbers of classes and class size balance. Through a series of experiments we show that LI is a better predictor of the performance of GNNs on a dataset than homophily. We show that LI explains why GNNs can sometimes perform well on heterophilous datasets - a phenomenon recently observed in the literature.