A Fair Evaluation of Graph Foundation Models for Node Property Prediction

Due to the wide use of graph-structured data in different fields of industry and science, the development of Graph Foundation Models (GFMs) has recently attracted a lot of attention. While many different types of models are called GFMs, particular interest has been paid to GFMs designed for node property prediction tasks, which is one of the most popular settings in Graph ML with lots of real-world applications from fraud detection in financial and social networks to recommendation systems for e-commerce and user-generated content platforms. While a number of GFMs for this task have been recently proposed, the field has not converged to a unified evaluation setting, and different works evaluate their models in widely different ways, preventing reliable comparison of GFMs with each other and with other types of models. In this work, we conduct a fair and rigorous reevaluation of 9 recent GFMs for node property prediction, comparing them to strong Graph Neural Network (GNN) baselines. We find that, among these GFMs, only the most recent ones based on the Prior-data Fitted Networks paradigm outperform well-tuned GNNs in predictive performance, although at a higher inference cost.

Cluster Attention for Graph Machine Learning

Message Passing Neural Networks have recently become the most popular approach to graph machine learning tasks; however, their receptive field is limited by the number of message passing layers. To increase the receptive field, Graph Transformers with global attention have been proposed; however, global attention does not take into account the graph topology and thus lacks graph-structure-based inductive biases, which are typically very important for graph machine learning tasks. In this work, we propose an alternative approach: cluster attention (CLATT). We divide graph nodes into clusters with off-the-shelf graph community detection algorithms and let each node attend to all other nodes in each cluster. CLATT provides large receptive fields while still having strong graph-structure-based inductive biases. We show that augmenting Message Passing Neural Networks or Graph Transformers with CLATT significantly improves their performance on a wide range of graph datasets including datasets from the recently introduced GraphLand benchmark representing real-world applications of graph machine learning.

Fine-Grained Urban Traffic Forecasting on Metropolis-Scale Road Networks

Traffic forecasting on road networks is a complex task of significant practical importance that has recently attracted considerable attention from the machine learning community, with spatiotemporal graph neural networks (GNNs) becoming the most popular approach. The proper evaluation of traffic forecasting methods requires realistic datasets, but current publicly available benchmarks have significant drawbacks, including the absence of information about road connectivity for road graph construction, limited information about road properties, and a relatively small number of road segments that falls short of real-world applications. Further, current datasets mostly contain information about intercity highways with sparsely located sensors, while city road networks arguably present a more challenging forecasting task due to much denser roads and more complex urban traffic patterns. In this work, we provide a more complete, realistic, and challenging benchmark for traffic forecasting by releasing datasets representing the road networks of two major cities, with the largest containing almost 100,000 road segments (more than a 10-fold increase relative to existing datasets). Our datasets contain rich road features and provide fine-grained data about both traffic volume and traffic speed, allowing for building more holistic traffic forecasting systems. We show that most current implementations of neural spatiotemporal models for traffic forecasting have problems scaling to datasets of our size. To overcome this issue, we propose an alternative approach to neural traffic forecasting that uses a GNN without a dedicated module for temporal sequence processing, thus achieving much better scalability, while also demonstrating stronger forecasting performance. We hope our datasets and modeling insights will serve as a valuable resource for research in traffic forecasting.

Turning Tabular Foundation Models into Graph Foundation Models

While foundation models have revolutionized such fields as natural language processing and computer vision, their application and potential within graph machine learning remain largely unexplored. One of the key challenges in designing graph foundation models (GFMs) is handling diverse node features that can vary across different graph datasets. Although many works on GFMs have been focused exclusively on text-attributed graphs, the problem of handling arbitrary features of other types in GFMs has not been fully addressed. However, this problem is not unique to the graph domain, as it also arises in the field of machine learning for tabular data. In this work, motivated by the recent success of tabular foundation models like TabPFNv2, we propose G2T-FM, a simple graph foundation model that employs TabPFNv2 as a backbone. Specifically, G2T-FM augments the original node features with neighborhood feature aggregation, adds structural embeddings, and then applies TabPFNv2 to the constructed node representations. Even in a fully in-context regime, our model achieves strong results, significantly outperforming publicly available GFMs and performing on par with well-tuned GNNs trained from scratch. Moreover, after finetuning, G2T-FM surpasses well-tuned GNN baselines, highlighting the potential of the proposed approach. More broadly, our paper reveals a previously overlooked direction of utilizing tabular foundation models for graph machine learning tasks.

TabGraphs: A Benchmark and Strong Baselines for Learning on Graphs with Tabular Node Features

Tabular machine learning is an important field for industry and science. In this field, table rows are usually treated as independent data samples, but additional information about relations between them is sometimes available and can be used to improve predictive performance. Such information can be naturally modeled with a graph, thus tabular machine learning may benefit from graph machine learning methods. However, graph machine learning models are typically evaluated on datasets with homogeneous node features, which have little in common with heterogeneous mixtures of numerical and categorical features present in tabular datasets. Thus, there is a critical difference between the data used in tabular and graph machine learning studies, which does not allow one to understand how successfully graph models can be transferred to tabular data. To bridge this gap, we propose a new benchmark of diverse graphs with heterogeneous tabular node features and realistic prediction tasks. We use this benchmark to evaluate a vast set of models, including simple methods previously overlooked in the literature. Our experiments show that graph neural networks (GNNs) can indeed often bring gains in predictive performance for tabular data, but standard tabular models also can be adapted to work with graph data by using simple feature preprocessing, which sometimes enables them to compete with and even outperform GNNs. Based on our empirical study, we provide insights for researchers and practitioners in both tabular and graph machine learning fields.

A critical look at the evaluation of GNNs under heterophily: are we really making progress?

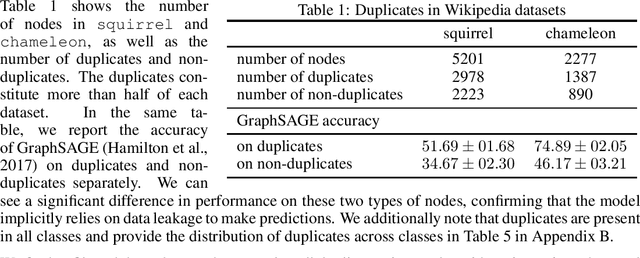
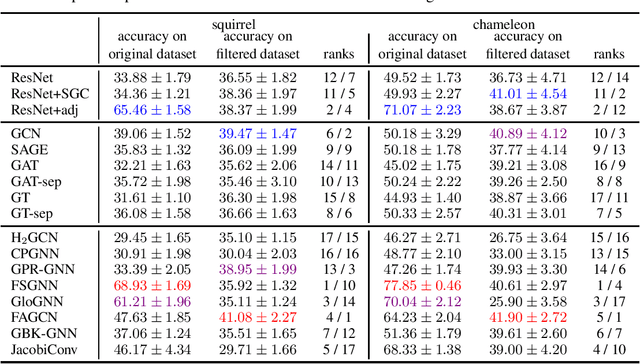
Node classification is a classical graph representation learning task on which Graph Neural Networks (GNNs) have recently achieved strong results. However, it is often believed that standard GNNs only work well for homophilous graphs, i.e., graphs where edges tend to connect nodes of the same class. Graphs without this property are called heterophilous, and it is typically assumed that specialized methods are required to achieve strong performance on such graphs. In this work, we challenge this assumption. First, we show that the standard datasets used for evaluating heterophily-specific models have serious drawbacks, making results obtained by using them unreliable. The most significant of these drawbacks is the presence of a large number of duplicate nodes in the datsets Squirrel and Chameleon, which leads to train-test data leakage. We show that removing duplicate nodes strongly affects GNN performance on these datasets. Then, we propose a set of heterophilous graphs of varying properties that we believe can serve as a better benchmark for evaluating the performance of GNNs under heterophily. We show that standard GNNs achieve strong results on these heterophilous graphs, almost always outperforming specialized models. Our datasets and the code for reproducing our experiments are available at https://github.com/yandex-research/heterophilous-graphs

Characterizing Graph Datasets for Node Classification: Beyond Homophily-Heterophily Dichotomy

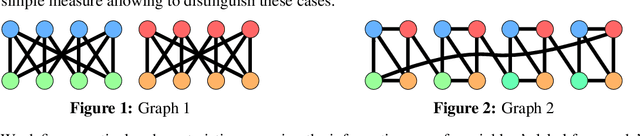
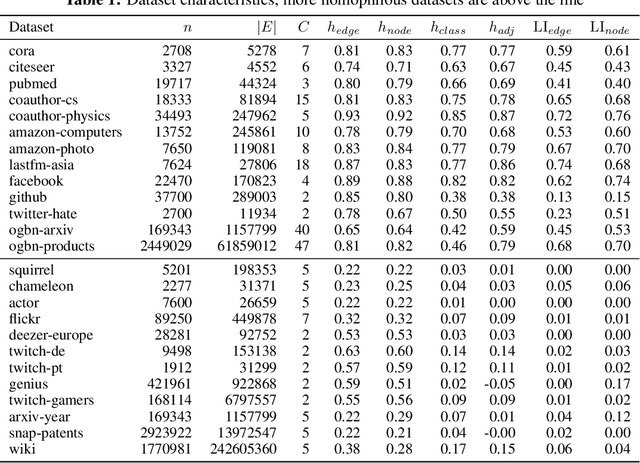
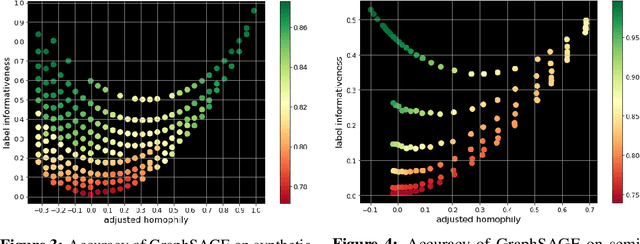
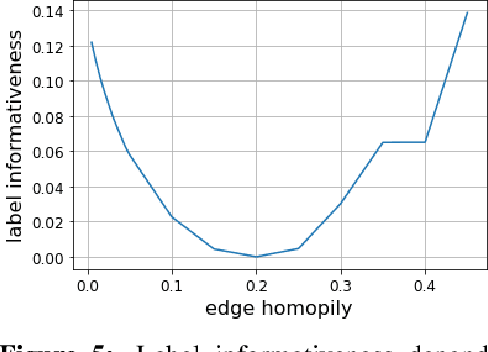
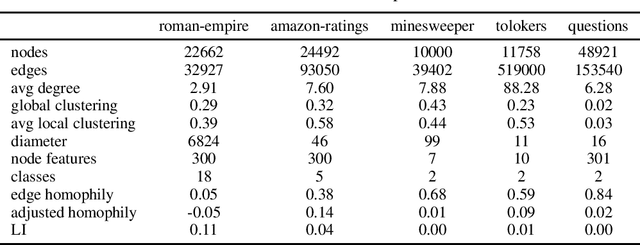
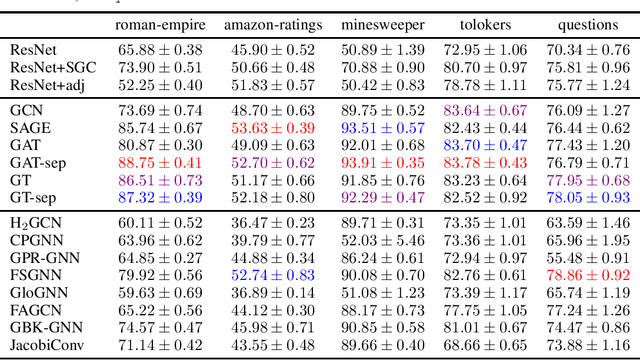
Homophily is a graph property describing the tendency of edges to connect similar nodes; the opposite is called heterophily. While homophily is natural for many real-world networks, there are also networks without this property. It is often believed that standard message-passing graph neural networks (GNNs) do not perform well on non-homophilous graphs, and thus such datasets need special attention. While a lot of effort has been put into developing graph representation learning methods for heterophilous graphs, there is no universally agreed upon measure of homophily. Several metrics for measuring homophily have been used in the literature, however, we show that all of them have critical drawbacks preventing comparison of homophily levels between different datasets. We formalize desirable properties for a proper homophily measure and show how existing literature on the properties of classification performance metrics can be linked to our problem. In doing so we find a measure that we call adjusted homophily that satisfies more desirable properties than existing homophily measures. Interestingly, this measure is related to two classification performance metrics - Cohen's Kappa and Matthews correlation coefficient. Then, we go beyond the homophily-heterophily dichotomy and propose a new property that we call label informativeness (LI) that characterizes how much information a neighbor's label provides about a node's label. We theoretically show that LI is comparable across datasets with different numbers of classes and class size balance. Through a series of experiments we show that LI is a better predictor of the performance of GNNs on a dataset than homophily. We show that LI explains why GNNs can sometimes perform well on heterophilous datasets - a phenomenon recently observed in the literature.