A Notion of Feature Importance by Decorrelation and Detection of Trends by Random Forest Regression

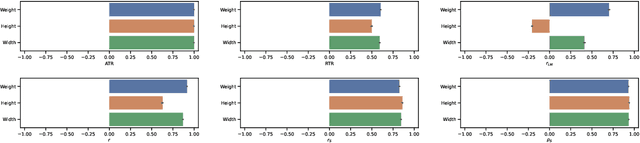
In many studies, we want to determine the influence of certain features on a dependent variable. More specifically, we are interested in the strength of the influence -- i.e., is the feature relevant? -- and, if so, how the feature influences the dependent variable. Recently, data-driven approaches such as \emph{random forest regression} have found their way into applications (Boulesteix et al., 2012). These models allow to directly derive measures of feature importance, which are a natural indicator of the strength of the influence. For the relevant features, the correlation or rank correlation between the feature and the dependent variable has typically been used to determine the nature of the influence. More recent methods, some of which can also measure interactions between features, are based on a modeling approach. In particular, when machine learning models are used, SHAP scores are a recent and prominent method to determine these trends (Lundberg et al., 2017). In this paper, we introduce a novel notion of feature importance based on the well-studied Gram-Schmidt decorrelation method. Furthermore, we propose two estimators for identifying trends in the data using random forest regression, the so-called absolute and relative transversal rate. We empirically compare the properties of our estimators with those of well-established estimators on a variety of synthetic and real-world datasets.

Inference of a Rumor's Source in the Independent Cascade Model

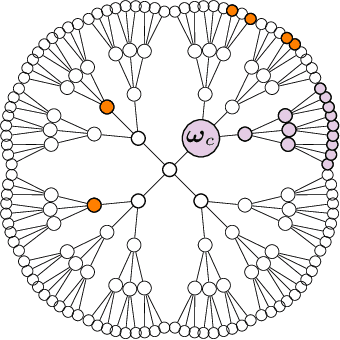
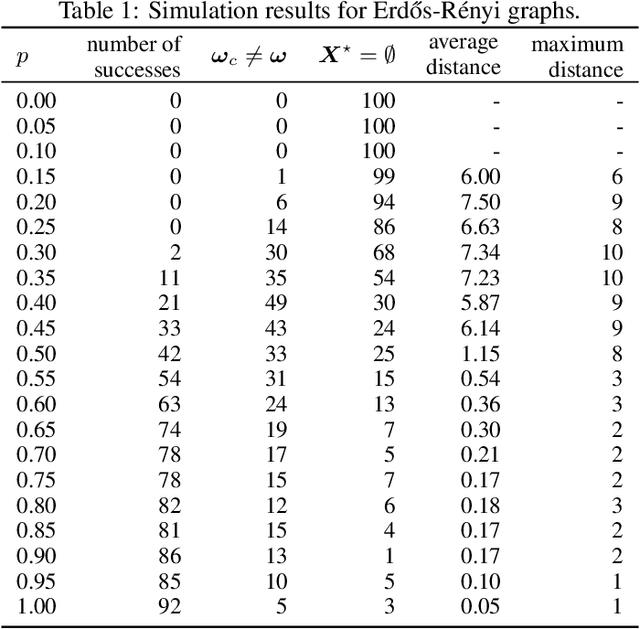
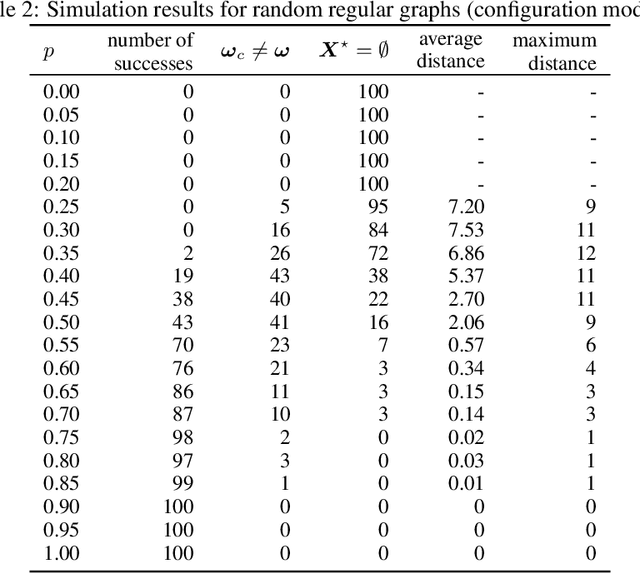
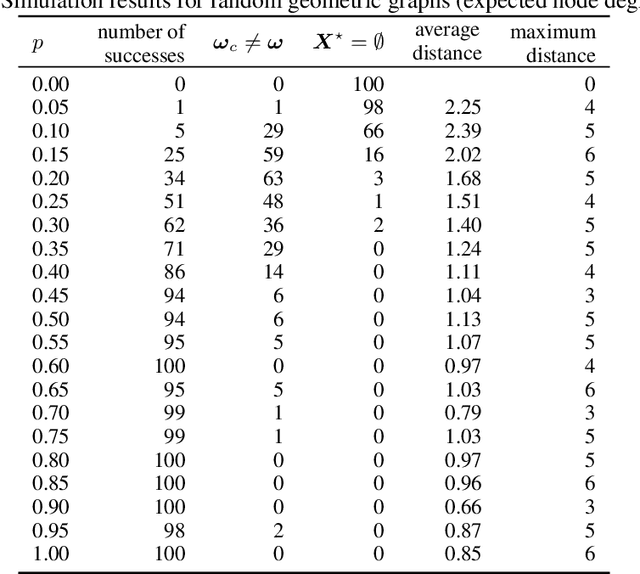
We consider the so-called Independent Cascade Model for rumor spreading or epidemic processes popularized by Kempe et al.\ [2003]. In this model, a small subset of nodes from a network are the source of a rumor. In discrete time steps, each informed node "infects" each of its uninformed neighbors with probability $p$. While many facets of this process are studied in the literature, less is known about the inference problem: given a number of infected nodes in a network, can we learn the source of the rumor? In the context of epidemiology this problem is often referred to as patient zero problem. It belongs to a broader class of problems where the goal is to infer parameters of the underlying spreading model, see, e.g., Lokhov [NeurIPS'16] or Mastakouri et al. [NeurIPS'20]. In this work we present a maximum likelihood estimator for the rumor's source, given a snapshot of the process in terms of a set of active nodes $X$ after $t$ steps. Our results show that, for cycle-free graphs, the likelihood estimator undergoes a non-trivial phase transition as a function $t$. We provide a rigorous analysis for two prominent classes of acyclic network, namely $d$-regular trees and Galton-Watson trees, and verify empirically that our heuristics work well in various general networks.