Efficient Approximate Recovery from Pooled Data Using Doubly Regular Pooling Schemes

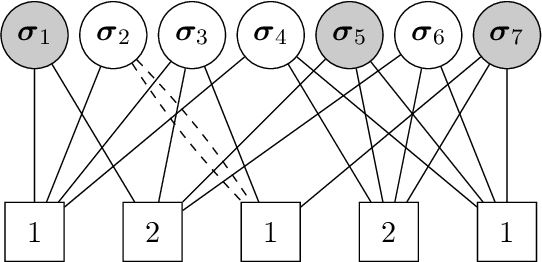
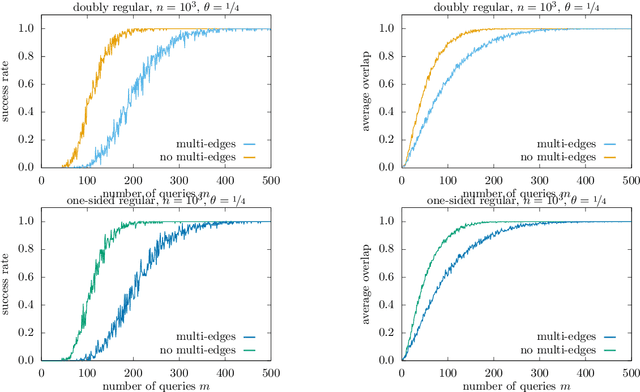
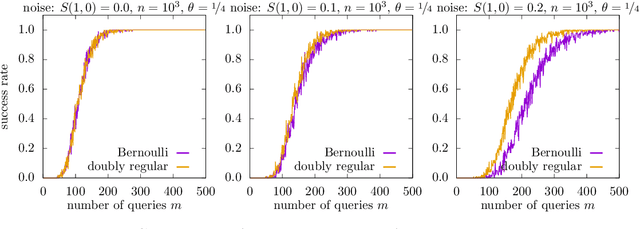
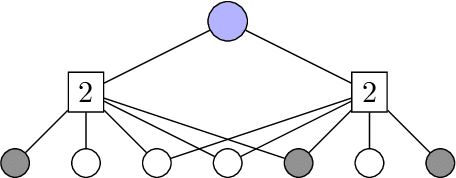
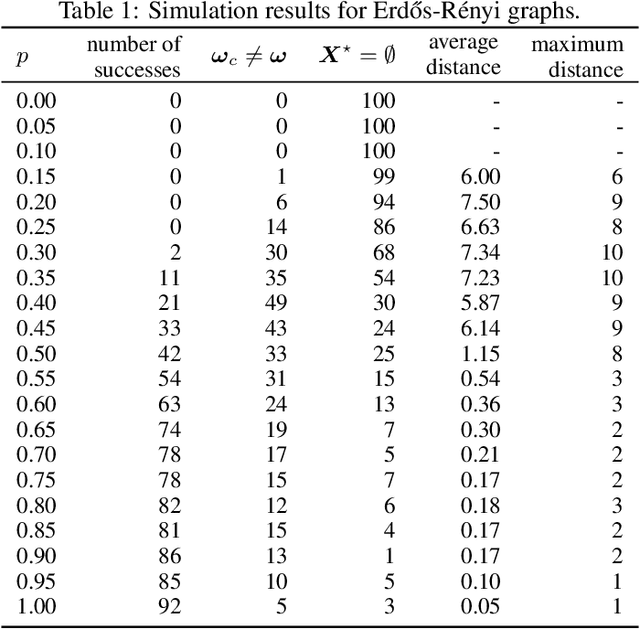
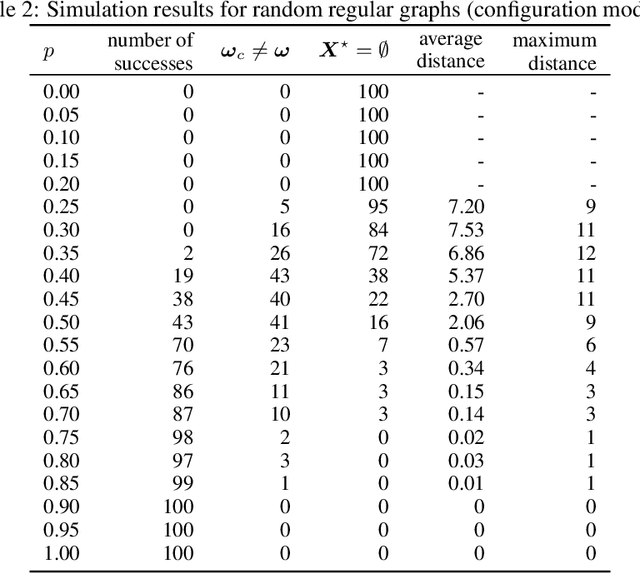
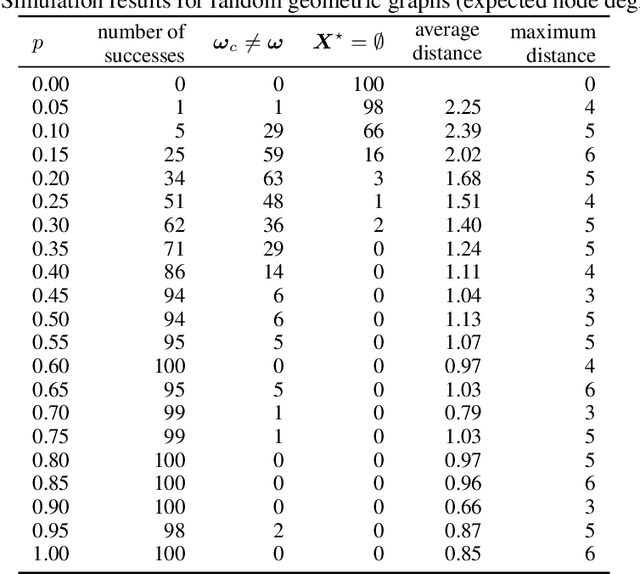
In the pooled data problem we are given $n$ agents with hidden state bits, either $0$ or $1$. The hidden states are unknown and can be seen as the underlying ground truth $\sigma$. To uncover that ground truth, we are given a querying method that queries multiple agents at a time. Each query reports the sum of the states of the queried agents. Our goal is to learn the hidden state bits using as few queries as possible. So far, most literature deals with exact reconstruction of all hidden state bits. We study a more relaxed variant in which we allow a small fraction of agents to be classified incorrectly. This becomes particularly relevant in the noisy variant of the pooled data problem where the queries' results are subject to random noise. In this setting, we provide a doubly regular test design that assigns agents to queries. For this design we analyze an approximate reconstruction algorithm that estimates the hidden bits in a greedy fashion. We give a rigorous analysis of the algorithm's performance, its error probability, and its approximation quality. As a main technical novelty, our analysis is uniform in the degree of noise and the sparsity of $\sigma$. Finally, simulations back up our theoretical findings and provide strong empirical evidence that our algorithm works well for realistic sample sizes.

Inference of a Rumor's Source in the Independent Cascade Model

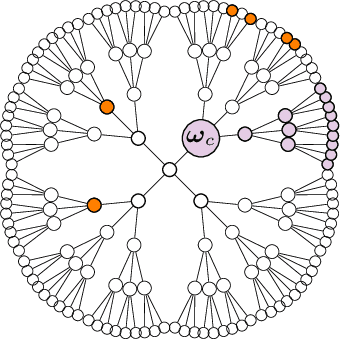
We consider the so-called Independent Cascade Model for rumor spreading or epidemic processes popularized by Kempe et al.\ [2003]. In this model, a small subset of nodes from a network are the source of a rumor. In discrete time steps, each informed node "infects" each of its uninformed neighbors with probability $p$. While many facets of this process are studied in the literature, less is known about the inference problem: given a number of infected nodes in a network, can we learn the source of the rumor? In the context of epidemiology this problem is often referred to as patient zero problem. It belongs to a broader class of problems where the goal is to infer parameters of the underlying spreading model, see, e.g., Lokhov [NeurIPS'16] or Mastakouri et al. [NeurIPS'20]. In this work we present a maximum likelihood estimator for the rumor's source, given a snapshot of the process in terms of a set of active nodes $X$ after $t$ steps. Our results show that, for cycle-free graphs, the likelihood estimator undergoes a non-trivial phase transition as a function $t$. We provide a rigorous analysis for two prominent classes of acyclic network, namely $d$-regular trees and Galton-Watson trees, and verify empirically that our heuristics work well in various general networks.