Improved Reconstruction of Random Geometric Graphs
Paper and Code
Jul 29, 2021
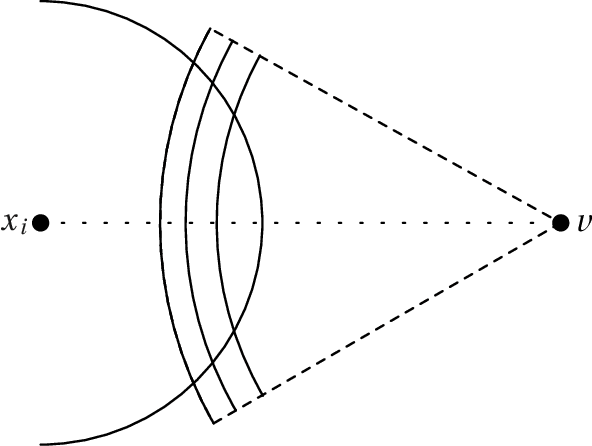
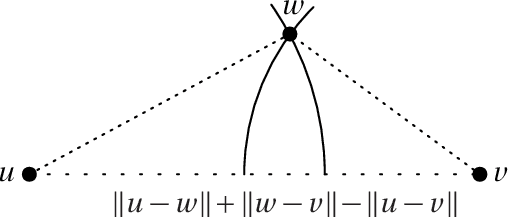
Embedding graphs in a geographical or latent space, i.e., inferring locations for vertices in Euclidean space or on a smooth submanifold, is a common task in network analysis, statistical inference, and graph visualization. We consider the classic model of random geometric graphs where $n$ points are scattered uniformly in a square of area $n$, and two points have an edge between them if and only if their Euclidean distance is less than $r$. The reconstruction problem then consists of inferring the vertex positions, up to symmetry, given only the adjacency matrix of the resulting graph. We give an algorithm that, if $r=n^\alpha$ for $\alpha > 0$, with high probability reconstructs the vertex positions with a maximum error of $O(n^\beta)$ where $\beta=1/2-(4/3)\alpha$, until $\alpha \ge 3/8$ where $\beta=0$ and the error becomes $O(\sqrt{\log n})$. This improves over earlier results, which were unable to reconstruct with error less than $r$. Our method estimates Euclidean distances using a hybrid of graph distances and short-range estimates based on the number of common neighbors. We sketch proofs that our results also apply on the surface of a sphere, and (with somewhat different exponents) in any fixed dimension.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge