Thomas P. Hayes
Improved Reconstruction of Random Geometric Graphs
Jul 29, 2021
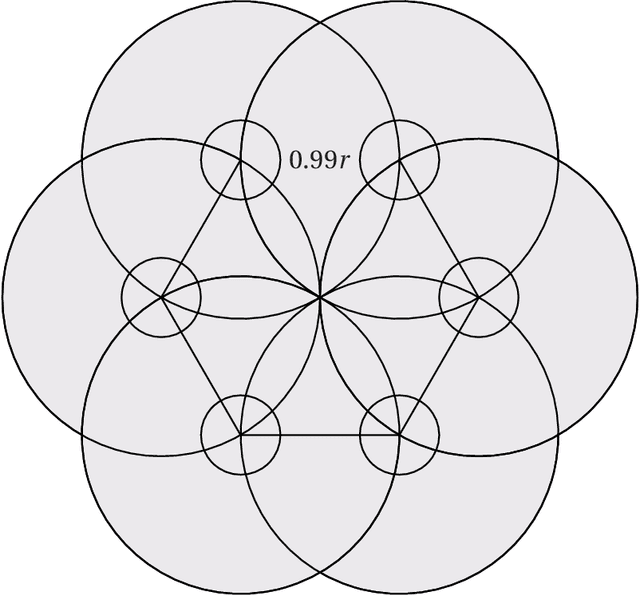
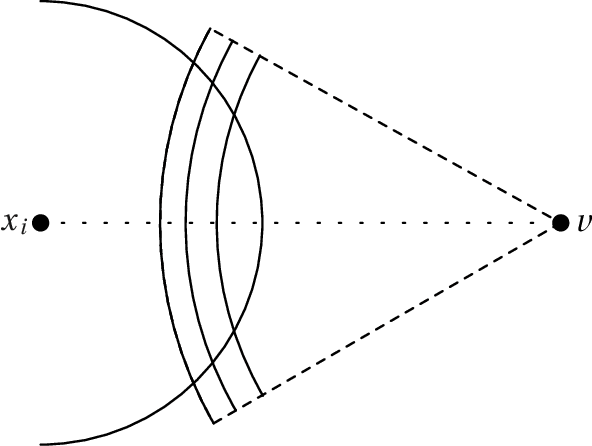
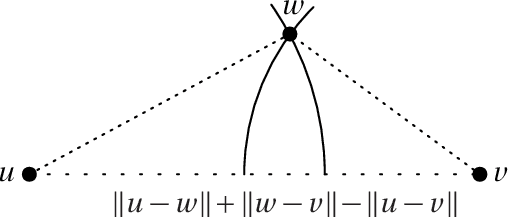
Abstract:Embedding graphs in a geographical or latent space, i.e., inferring locations for vertices in Euclidean space or on a smooth submanifold, is a common task in network analysis, statistical inference, and graph visualization. We consider the classic model of random geometric graphs where $n$ points are scattered uniformly in a square of area $n$, and two points have an edge between them if and only if their Euclidean distance is less than $r$. The reconstruction problem then consists of inferring the vertex positions, up to symmetry, given only the adjacency matrix of the resulting graph. We give an algorithm that, if $r=n^\alpha$ for $\alpha > 0$, with high probability reconstructs the vertex positions with a maximum error of $O(n^\beta)$ where $\beta=1/2-(4/3)\alpha$, until $\alpha \ge 3/8$ where $\beta=0$ and the error becomes $O(\sqrt{\log n})$. This improves over earlier results, which were unable to reconstruct with error less than $r$. Our method estimates Euclidean distances using a hybrid of graph distances and short-range estimates based on the number of common neighbors. We sketch proofs that our results also apply on the surface of a sphere, and (with somewhat different exponents) in any fixed dimension.
Fully-Asynchronous Distributed Metropolis Sampler with Optimal Speedup
Apr 01, 2019Abstract:The Metropolis-Hastings algorithm is a fundamental Markov chain Monte Carlo (MCMC) method for sampling and inference. With the advent of Big Data, distributed and parallel variants of MCMC methods are attracting increased attention. In this paper, we give a distributed algorithm that can correctly simulate sequential single-site Metropolis chains without any bias in a fully asynchronous message-passing model. Furthermore, if a natural Lipschitz condition is satisfied by the Metropolis filters, our algorithm can simulate $N$-step Metropolis chains within $O(N/n+\log n)$ rounds of asynchronous communications, where $n$ is the number of variables. For sequential single-site dynamics, whose mixing requires $\Omega(n\log n)$ steps, this achieves an optimal linear speedup. For several well-studied important graphical models, including proper graph coloring, hardcore model, and Ising model, the condition for linear speedup is weaker than the respective uniqueness (mixing) conditions. The novel idea in our algorithm is to resolve updates in advance: the local Metropolis filters can be executed correctly before the full information about neighboring spins is available. This achieves optimal parallelism of Metropolis processes without introducing any bias.
Block Coordinate Descent for Sparse NMF
Mar 18, 2013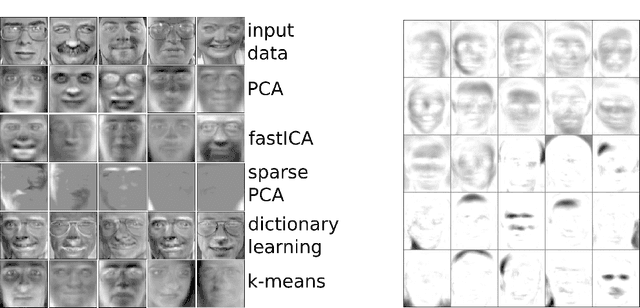
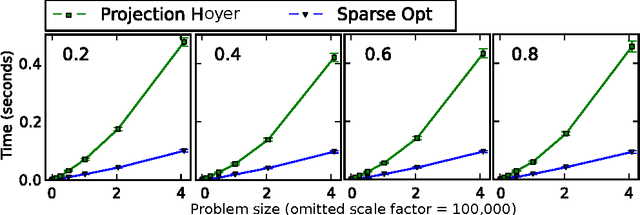
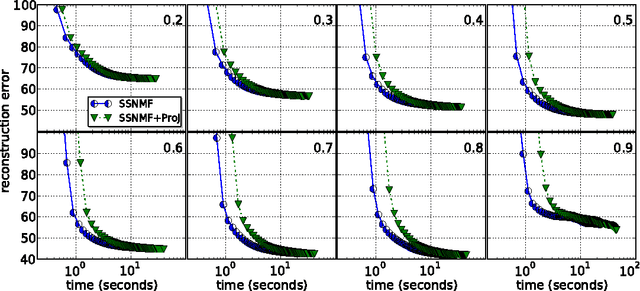
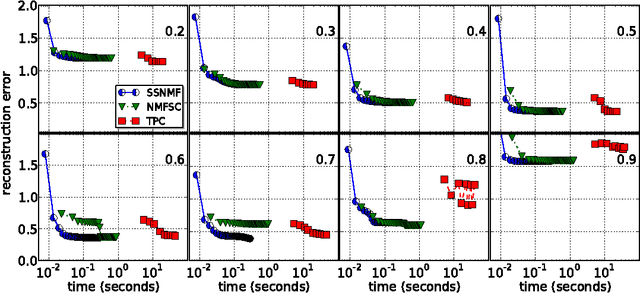
Abstract:Nonnegative matrix factorization (NMF) has become a ubiquitous tool for data analysis. An important variant is the sparse NMF problem which arises when we explicitly require the learnt features to be sparse. A natural measure of sparsity is the L$_0$ norm, however its optimization is NP-hard. Mixed norms, such as L$_1$/L$_2$ measure, have been shown to model sparsity robustly, based on intuitive attributes that such measures need to satisfy. This is in contrast to computationally cheaper alternatives such as the plain L$_1$ norm. However, present algorithms designed for optimizing the mixed norm L$_1$/L$_2$ are slow and other formulations for sparse NMF have been proposed such as those based on L$_1$ and L$_0$ norms. Our proposed algorithm allows us to solve the mixed norm sparsity constraints while not sacrificing computation time. We present experimental evidence on real-world datasets that shows our new algorithm performs an order of magnitude faster compared to the current state-of-the-art solvers optimizing the mixed norm and is suitable for large-scale datasets.
How to Beat the Adaptive Multi-Armed Bandit
Feb 14, 2006Abstract:The multi-armed bandit is a concise model for the problem of iterated decision-making under uncertainty. In each round, a gambler must pull one of $K$ arms of a slot machine, without any foreknowledge of their payouts, except that they are uniformly bounded. A standard objective is to minimize the gambler's regret, defined as the gambler's total payout minus the largest payout which would have been achieved by any fixed arm, in hindsight. Note that the gambler is only told the payout for the arm actually chosen, not for the unchosen arms. Almost all previous work on this problem assumed the payouts to be non-adaptive, in the sense that the distribution of the payout of arm $j$ in round $i$ is completely independent of the choices made by the gambler on rounds $1, \dots, i-1$. In the more general model of adaptive payouts, the payouts in round $i$ may depend arbitrarily on the history of past choices made by the algorithm. We present a new algorithm for this problem, and prove nearly optimal guarantees for the regret against both non-adaptive and adaptive adversaries. After $T$ rounds, our algorithm has regret $O(\sqrt{T})$ with high probability (the tail probability decays exponentially). This dependence on $T$ is best possible, and matches that of the full-information version of the problem, in which the gambler is told the payouts for all $K$ arms after each round. Previously, even for non-adaptive payouts, the best high-probability bounds known were $O(T^{2/3})$, due to Auer, Cesa-Bianchi, Freund and Schapire. The expected regret of their algorithm is $O(T^{1/2}) for non-adaptive payouts, but as we show, $\Omega(T^{2/3})$ for adaptive payouts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge