Approximate sampling and estimation of partition functions using neural networks

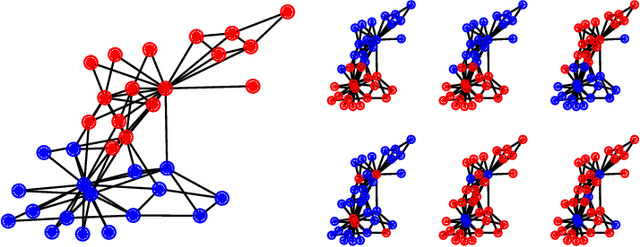
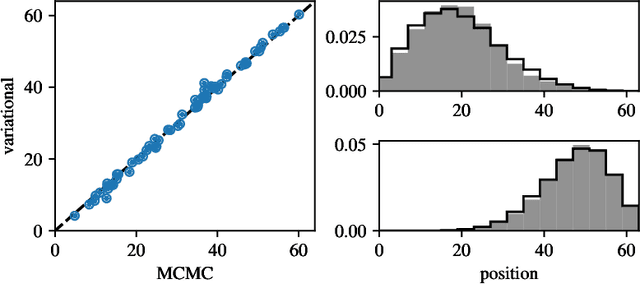
We consider the closely related problems of sampling from a distribution known up to a normalizing constant, and estimating said normalizing constant. We show how variational autoencoders (VAEs) can be applied to this task. In their standard applications, VAEs are trained to fit data drawn from an intractable distribution. We invert the logic and train the VAE to fit a simple and tractable distribution, on the assumption of a complex and intractable latent distribution, specified up to normalization. This procedure constructs approximations without the use of training data or Markov chain Monte Carlo sampling. We illustrate our method on three examples: the Ising model, graph clustering, and ranking.

Belief propagation for permutations, rankings, and partial orders

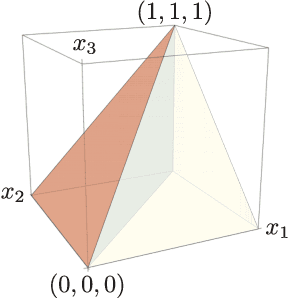
Many datasets give partial information about an ordering or ranking by indicating which team won a game, which item a user prefers, or who infected whom. We define a continuous spin system whose Gibbs distribution is the posterior distribution on permutations, given a probabilistic model of these interactions. Using the cavity method we derive a belief propagation algorithm that computes the marginal distribution of each node's position. In addition, the Bethe free energy lets us approximate the number of linear extensions of a partial order and perform model selection.

Message passing for probabilistic models on networks with loops

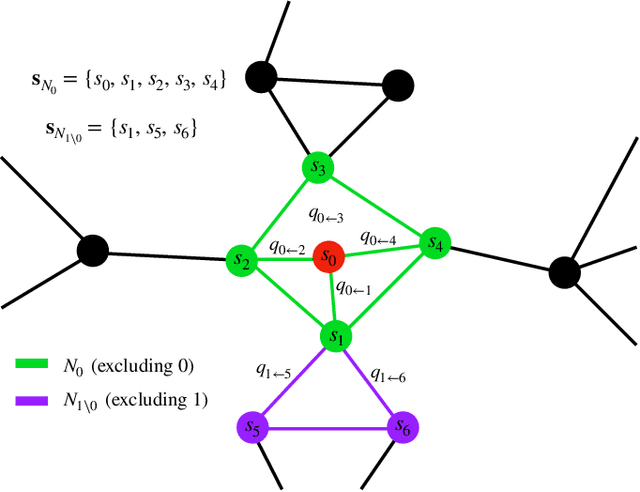
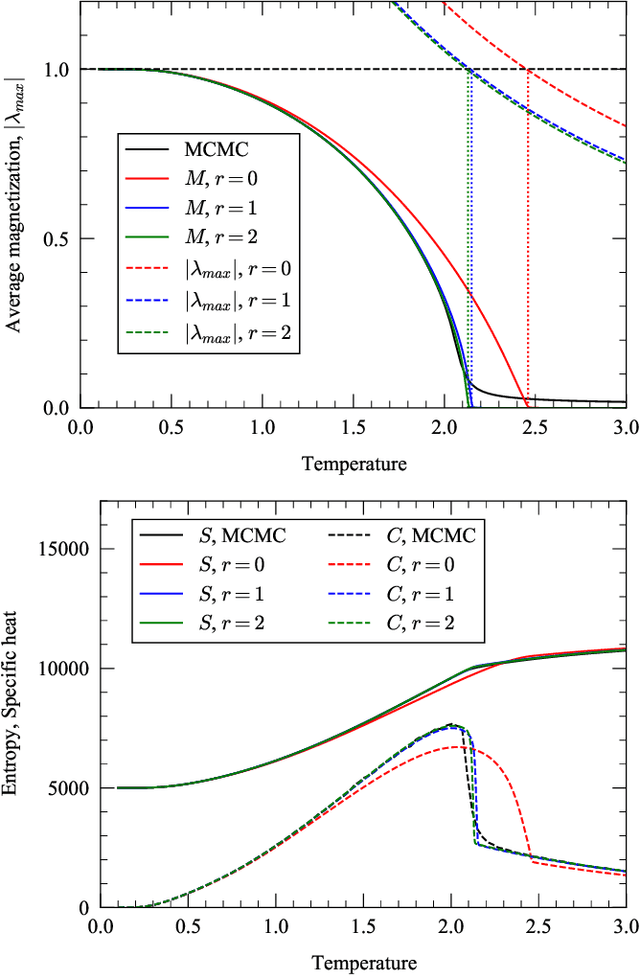
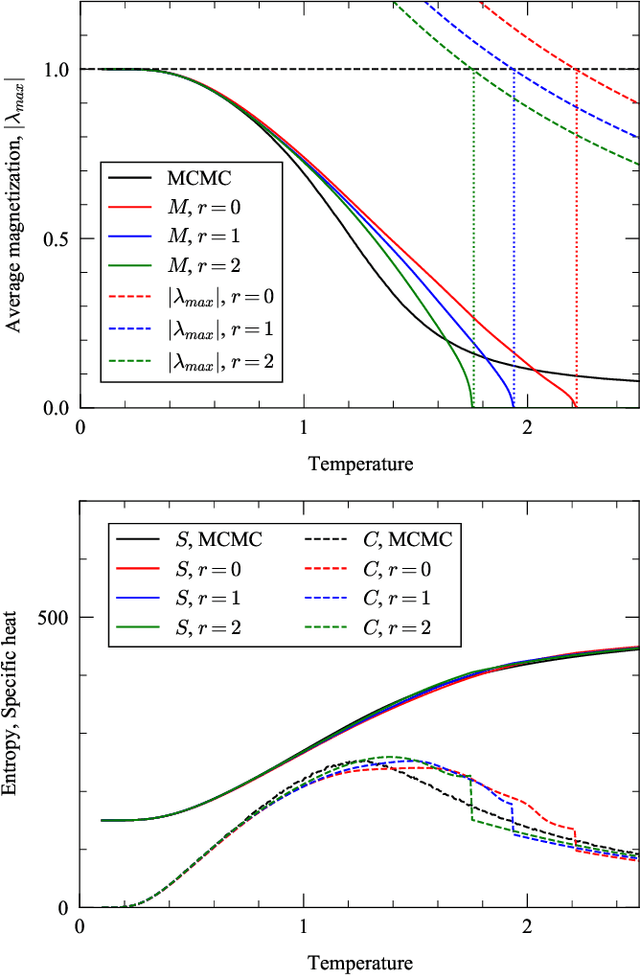
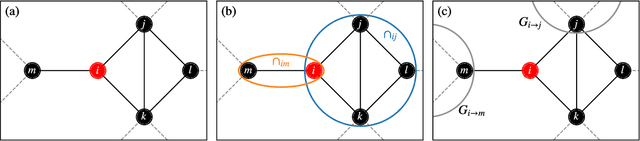
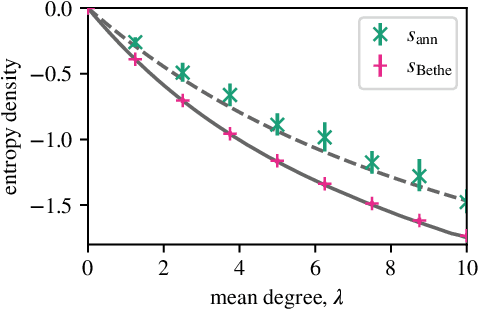
In this paper, we extend a recently proposed framework for message passing on "loopy" networks to the solution of probabilistic models. We derive a self-consistent set of message passing equations that allow for fast computation of probability distributions in systems that contain short loops, potentially with high density, as well as expressions for the entropy and partition function of such systems, which are notoriously difficult quantities to compute. Using the Ising model as an example, we show that our solutions are asymptotically exact on certain classes of networks with short loops and offer a good approximation on more general networks, improving significantly on results derived from standard belief propagation. We also discuss potential applications of our method to a variety of other problems.

Improved mutual information measure for classification and community detection

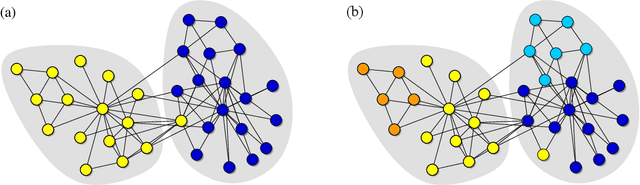
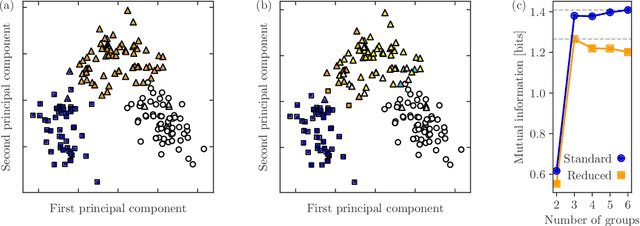
The information theoretic quantity known as mutual information finds wide use in classification and community detection analyses to compare two classifications of the same set of objects into groups. In the context of classification algorithms, for instance, it is often used to compare discovered classes to known ground truth and hence to quantify algorithm performance. Here we argue that the standard mutual information, as commonly defined, omits a crucial term which can become large under real-world conditions, producing results that can be substantially in error. We demonstrate how to correct this error and define a mutual information that works in all cases. We discuss practical implementation of the new measure and give some example applications.