Mixture models for data with unknown distributions

We describe and analyze a broad class of mixture models for real-valued multivariate data in which the probability density of observations within each component of the model is represented as an arbitrary combination of basis functions. Fits to these models give us a way to cluster data with distributions of unknown form, including strongly non-Gaussian or multimodal distributions, and return both a division of the data and an estimate of the distributions, effectively performing clustering and density estimation within each cluster at the same time. We describe two fitting methods, one using an expectation-maximization (EM) algorithm and the other a Bayesian non-parametric method using a collapsed Gibbs sampler. The former is numerically efficient, but gives only point estimates of the probability densities. The latter is more computationally demanding but returns a full Bayesian posterior and also an estimate of the number of components. We demonstrate our methods with a selection of illustrative applications and give code implementing both algorithms.

Fast sampling and model selection for Bayesian mixture models

We describe two Monte Carlo algorithms for sampling from the integrated posterior distributions of a range of Bayesian mixture models. Both algorithms allow us to directly sample not only the assignment of observations to components but also the number of components, thereby fitting the model and performing model selection over the number of components in a single computation. The first algorithm is a traditional collapsed Gibbs sampler, albeit with an unusual move-set; the second builds on the first, adding rejection-free sampling from the prior over component assignments, to create an algorithm that has excellent mixing time in typical applications and outperforms current state-of-the-art methods, in some cases by a wide margin. We demonstrate our methods with a selection of applications to latent class analysis.

Mutual information and the encoding of contingency tables

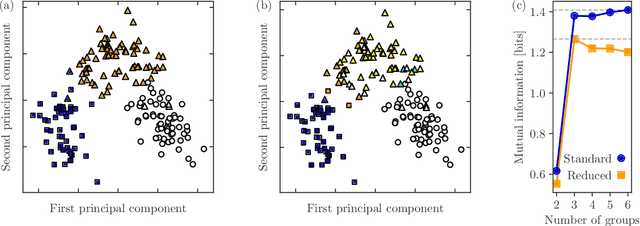
Mutual information is commonly used as a measure of similarity between competing labelings of a given set of objects, for example to quantify performance in classification and community detection tasks. As argued recently, however, the mutual information as conventionally defined can return biased results because it neglects the information cost of the so-called contingency table, a crucial component of the similarity calculation. In principle the bias can be rectified by subtracting the appropriate information cost, leading to the modified measure known as the reduced mutual information, but in practice one can only ever compute an upper bound on this information cost, and the value of the reduced mutual information depends crucially on how good a bound is established. In this paper we describe an improved method for encoding contingency tables that gives a substantially better bound in typical use cases, and approaches the ideal value in the common case where the labelings are closely similar, as we demonstrate with extensive numerical results.

Luck, skill, and depth of competition in games and social hierarchies

Patterns of wins and losses in pairwise contests, such as occur in sports and games, consumer research and paired comparison studies, and human and animal social hierarchies, are commonly analyzed using probabilistic models that allow one to quantify the strength of competitors or predict the outcome of future contests. Here we generalize this approach to incorporate two additional features: an element of randomness or luck that leads to upset wins, and a "depth of competition" variable that measures the complexity of a game or hierarchy. Fitting the resulting model to a large collection of data sets we estimate depth and luck in a range of games, sports, and social situations. In general, we find that social competition tends to be "deep," meaning it has a pronounced hierarchy with many distinct levels, but also that there is often a nonzero chance of an upset victory, meaning that dominance challenges can be won even by significant underdogs. Competition in sports and games, by contrast, tends to be shallow and in most cases there is little evidence of upset wins, beyond those already implied by the shallowness of the hierarchy.

Normalized mutual information is a biased measure for classification and community detection

Normalized mutual information is widely used as a similarity measure for evaluating the performance of clustering and classification algorithms. In this paper, we show that results returned by the normalized mutual information are biased for two reasons: first, because they ignore the information content of the contingency table and, second, because their symmetric normalization introduces spurious dependence on algorithm output. We introduce a modified version of the mutual information that remedies both of these shortcomings. As a practical demonstration of the importance of using an unbiased measure, we perform extensive numerical tests on a basket of popular algorithms for network community detection and show that one's conclusions about which algorithm is best are significantly affected by the biases in the traditional mutual information.

20 years of network community detection

A fundamental technical challenge in the analysis of network data is the automated discovery of communities - groups of nodes that are strongly connected or that share similar features or roles. In this commentary we review progress in the field over the last 20 years.

Fast computation of rankings from pairwise comparisons

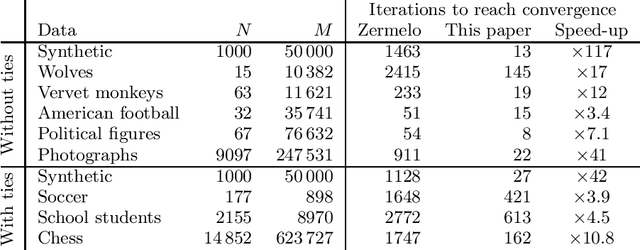
We study the ranking of individuals, teams, or objects on the basis of pairwise comparisons using the Bradley-Terry model. Maximum-likelihood estimates of rankings within this model are commonly made using a simple iterative algorithm first introduced by Zermelo almost a century ago. Here we describe an alternative and similarly simple iteration that solves the same problem much faster -- over a hundred times faster in some cases. We demonstrate this algorithm with applications to a range of example data sets and derive some results regarding its convergence.

Rankings from multimodal pairwise comparisons

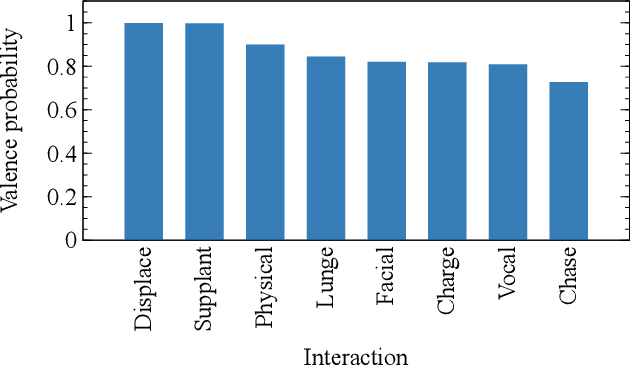
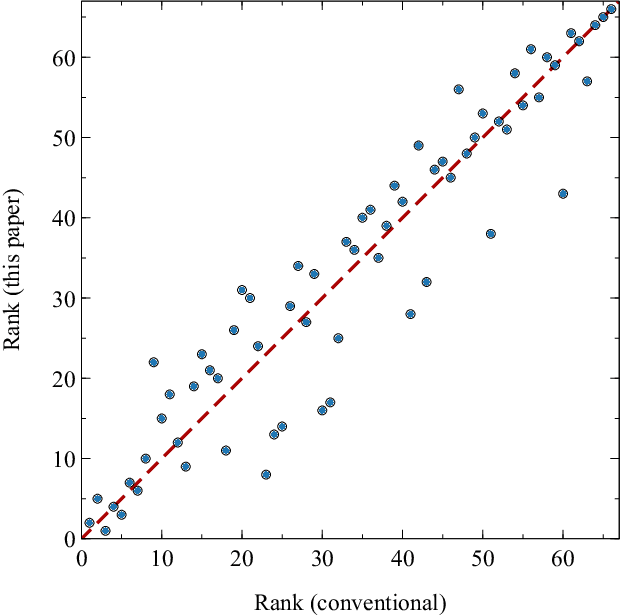
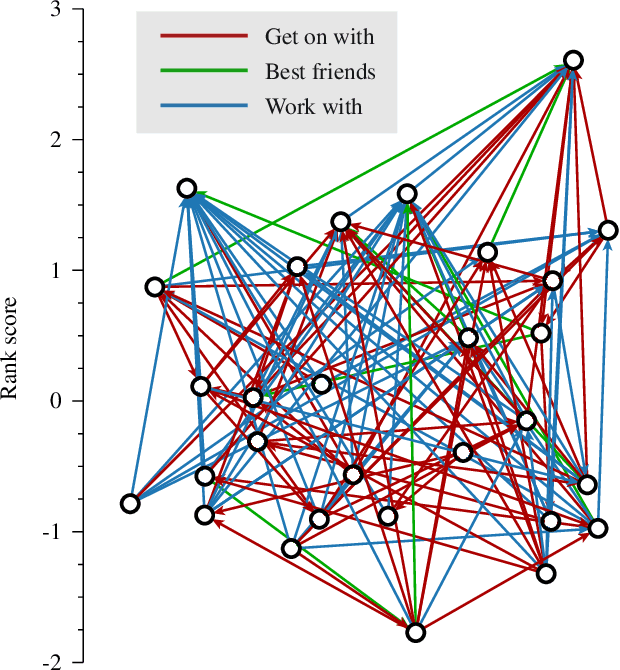
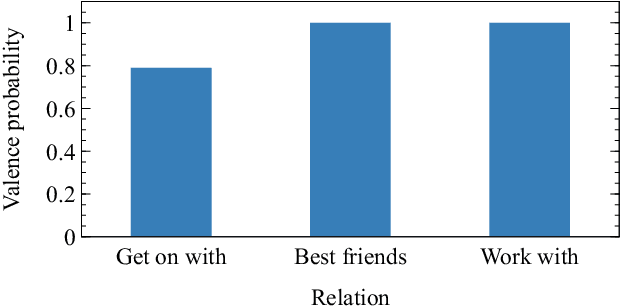
The task of ranking individuals or teams, based on a set of comparisons between pairs, arises in various contexts, including sporting competitions and the analysis of dominance hierarchies among animals and humans. Given data on which competitors beat which others, the challenge is to rank the competitors from best to worst. Here we study the problem of computing rankings when there are multiple, potentially conflicting modes of comparison, such as multiple types of dominance behaviors among animals. We assume that we do not know a priori what information each behavior conveys about the ranking, or even whether they convey any information at all. Nonetheless we show that it is possible to compute a ranking in this situation and present a fast method for doing so, based on a combination of an expectation-maximization algorithm and a modified Bradley-Terry model. We give a selection of example applications to both animal and human competition.

Message passing for probabilistic models on networks with loops

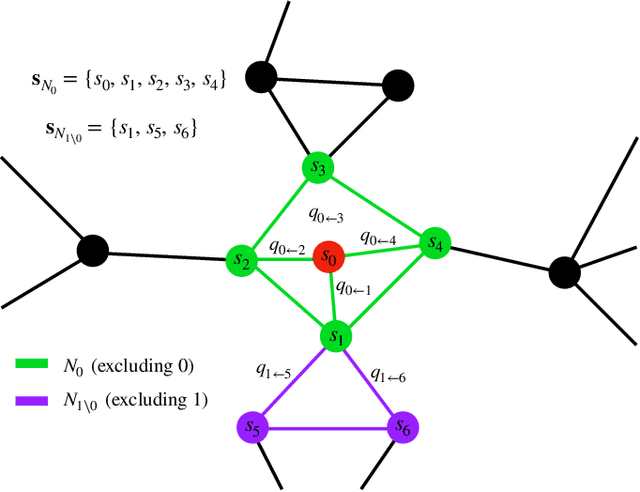
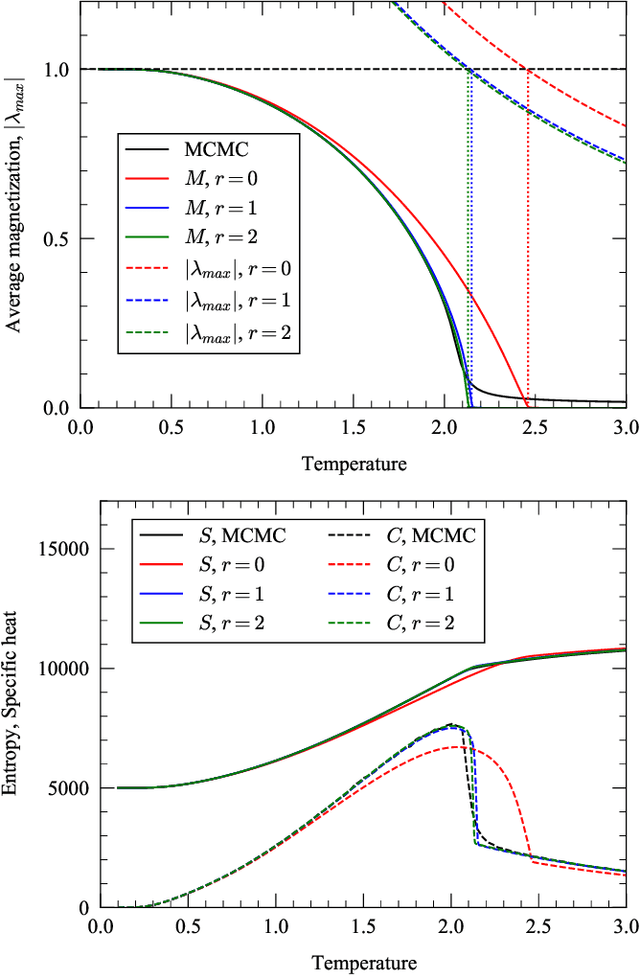
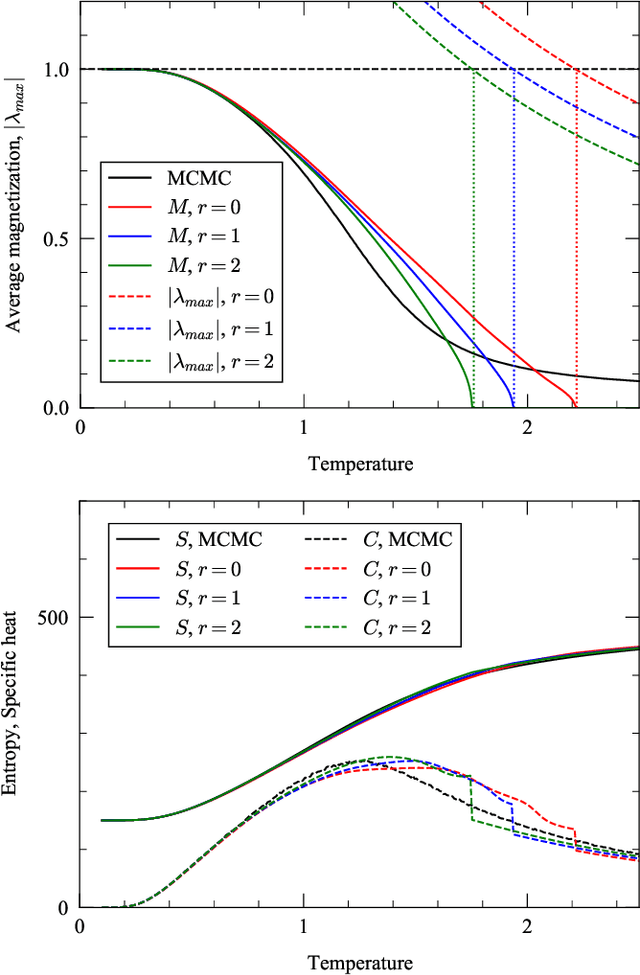
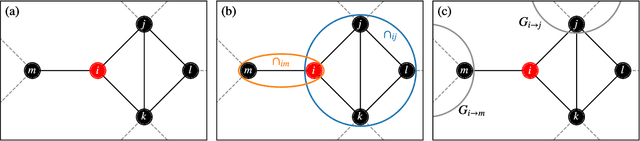
In this paper, we extend a recently proposed framework for message passing on "loopy" networks to the solution of probabilistic models. We derive a self-consistent set of message passing equations that allow for fast computation of probability distributions in systems that contain short loops, potentially with high density, as well as expressions for the entropy and partition function of such systems, which are notoriously difficult quantities to compute. Using the Ising model as an example, we show that our solutions are asymptotically exact on certain classes of networks with short loops and offer a good approximation on more general networks, improving significantly on results derived from standard belief propagation. We also discuss potential applications of our method to a variety of other problems.

Improved mutual information measure for classification and community detection

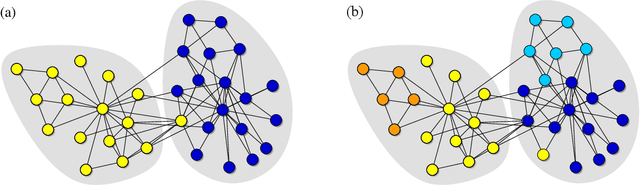
The information theoretic quantity known as mutual information finds wide use in classification and community detection analyses to compare two classifications of the same set of objects into groups. In the context of classification algorithms, for instance, it is often used to compare discovered classes to known ground truth and hence to quantify algorithm performance. Here we argue that the standard mutual information, as commonly defined, omits a crucial term which can become large under real-world conditions, producing results that can be substantially in error. We demonstrate how to correct this error and define a mutual information that works in all cases. We discuss practical implementation of the new measure and give some example applications.