MoRAX: Mobility-based Representation Augmentation for Geospatial Foundation Models

Geospatial Foundation Models (GFMs) are emerging as a powerful paradigm for learning semantically rich and geographically consistent visual and physical representations. However, their reliance on Earth-observation (EO) data leaves information about human activity largely underrepresented. Human mobility data reveals the functional and relational structure between regions that is missing from EO data, but is often limited only to the city where it is observed, making it challenging to use for transferable urban representation learning. We introduce MoRAX, a lightweight framework for augmenting geospatial embeddings with functional structure derived from human mobility. MoRAX preserves the coverage and consistency of a GFM while providing information about the functional connectivity among urban regions, permitting zero-shot deployment in unseen cities with or without available mobility data. Across four target cities spanning two countries, the MoRAX teacher model, which observes mobility, consistently outperforms GFMs and strong urban representation baselines in eight socioeconomic and environmental prediction tasks. Meanwhile, the student model, which never takes mobility data as input, approaches the teacher in performance on most tasks. Transfer results across countries further demonstrate that modulation conditioned on mobility flows provides a general mechanism for grounding geospatial foundations in the human dimension of cities.

Scalable inference of spatial regions and temporal signatures from time series

Regionalization aims to partition a spatial domain into contiguous regions that share similar characteristics, enabling more effective spatial analysis, policy making, and resource management. Existing approaches for spatial regionalization typically rely on static spatial snapshots rather than evolving time series. Meanwhile, most time series clustering methods ignore spatial structure or enforce spatial continuity through ad hoc regularization, constraining the number of inferred regions a priori either explicitly or implicitly. Utilizing the minimum description length principle from information theory, here we propose an efficient and fully nonparametric framework for the regionalization of spatial time series. Our method jointly infers a spatial partition along with a set of representative time series archetypes ("drivers") that best compress a spatiotemporal dataset, with a runtime log-linear in the number of time series. We demonstrate that this method can accurately recover planted regional structure and drivers in synthetic time series, and can extract meaningful structural regularities in large-scale empirical air quality and vegetation index records. Our method provides a principled and scalable framework for spatially contiguous partitioning, allowing interpretable temporal patterns and homogeneous regions to emerge directly from the data itself.

Learning when to rank: Estimation of partial rankings from sparse, noisy comparisons

A common task arising in various domains is that of ranking items based on the outcomes of pairwise comparisons, from ranking players and teams in sports to ranking products or brands in marketing studies and recommendation systems. Statistical inference-based methods such as the Bradley-Terry model, which extract rankings based on an underlying generative model of the comparison outcomes, have emerged as flexible and powerful tools to tackle the task of ranking in empirical data. In situations with limited and/or noisy comparisons, it is often challenging to confidently distinguish the performance of different items based on the evidence available in the data. However, existing inference-based ranking methods overwhelmingly choose to assign each item to a unique rank or score, suggesting a meaningful distinction when there is none. Here, we address this problem by developing a principled Bayesian methodology for learning partial rankings -- rankings with ties -- that distinguishes among the ranks of different items only when there is sufficient evidence available in the data. Our framework is adaptable to any statistical ranking method in which the outcomes of pairwise observations depend on the ranks or scores of the items being compared. We develop a fast agglomerative algorithm to perform Maximum A Posteriori (MAP) inference of partial rankings under our framework and examine the performance of our method on a variety of real and synthetic network datasets, finding that it frequently gives a more parsimonious summary of the data than traditional ranking, particularly when observations are sparse.

Mutual information and the encoding of contingency tables

Mutual information is commonly used as a measure of similarity between competing labelings of a given set of objects, for example to quantify performance in classification and community detection tasks. As argued recently, however, the mutual information as conventionally defined can return biased results because it neglects the information cost of the so-called contingency table, a crucial component of the similarity calculation. In principle the bias can be rectified by subtracting the appropriate information cost, leading to the modified measure known as the reduced mutual information, but in practice one can only ever compute an upper bound on this information cost, and the value of the reduced mutual information depends crucially on how good a bound is established. In this paper we describe an improved method for encoding contingency tables that gives a substantially better bound in typical use cases, and approaches the ideal value in the common case where the labelings are closely similar, as we demonstrate with extensive numerical results.

Normalized mutual information is a biased measure for classification and community detection

Normalized mutual information is widely used as a similarity measure for evaluating the performance of clustering and classification algorithms. In this paper, we show that results returned by the normalized mutual information are biased for two reasons: first, because they ignore the information content of the contingency table and, second, because their symmetric normalization introduces spurious dependence on algorithm output. We introduce a modified version of the mutual information that remedies both of these shortcomings. As a practical demonstration of the importance of using an unbiased measure, we perform extensive numerical tests on a basket of popular algorithms for network community detection and show that one's conclusions about which algorithm is best are significantly affected by the biases in the traditional mutual information.

Implicit models, latent compression, intrinsic biases, and cheap lunches in community detection

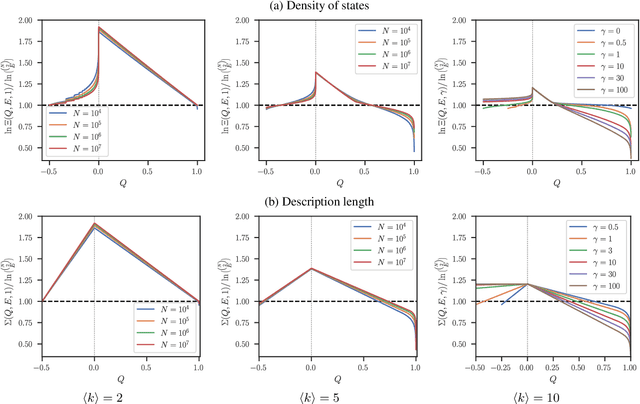
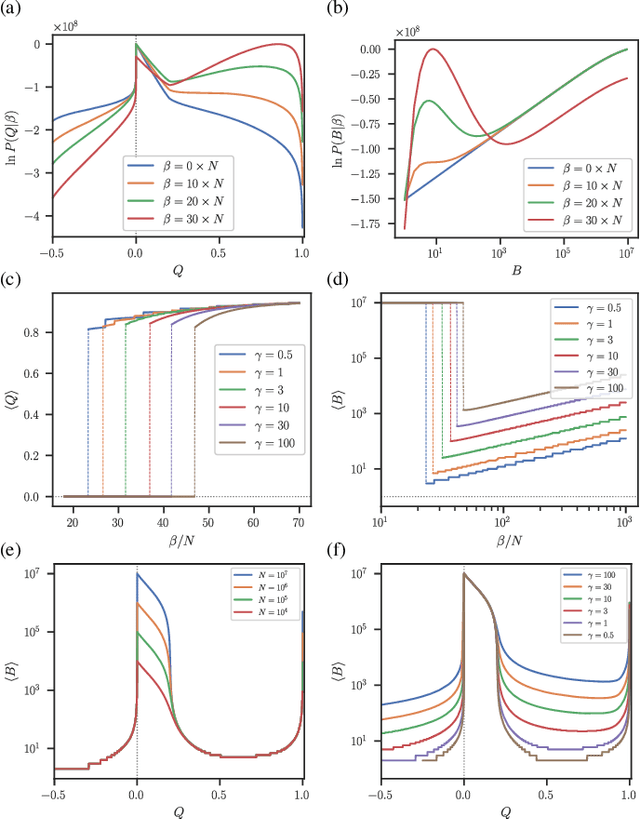
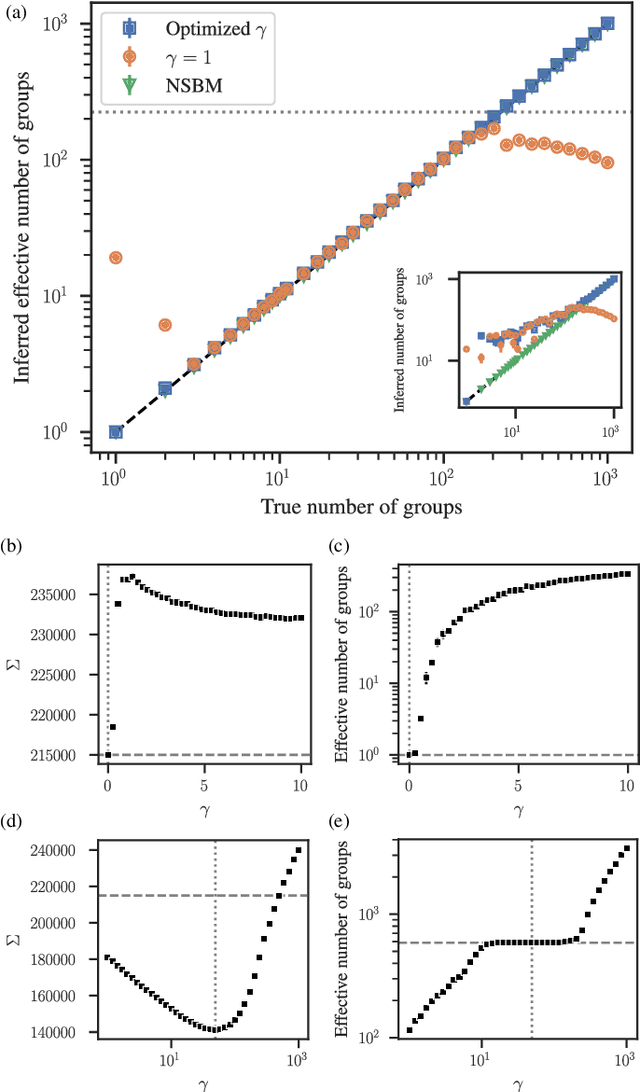
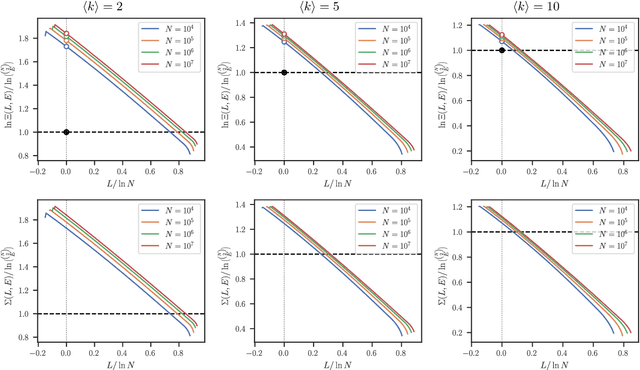
The task of community detection, which aims to partition a network into clusters of nodes to summarize its large-scale structure, has spawned the development of many competing algorithms with varying objectives. Some community detection methods are inferential, explicitly deriving the clustering objective through a probabilistic generative model, while other methods are descriptive, dividing a network according to an objective motivated by a particular application, making it challenging to compare these methods on the same scale. Here we present a solution to this problem that associates any community detection objective, inferential or descriptive, with its corresponding implicit network generative model. This allows us to compute the description length of a network and its partition under arbitrary objectives, providing a principled measure to compare the performance of different algorithms without the need for "ground truth" labels. Our approach also gives access to instances of the community detection problem that are optimal to any given algorithm, and in this way reveals intrinsic biases in popular descriptive methods, explaining their tendency to overfit. Using our framework, we compare a number of community detection methods on artificial networks, and on a corpus of over 500 structurally diverse empirical networks. We find that more expressive community detection methods exhibit consistently superior compression performance on structured data instances, without having degraded performance on a minority of situations where more specialized algorithms perform optimally. Our results undermine the implications of the "no free lunch" theorem for community detection, both conceptually and in practice, since it is confined to unstructured data instances, unlike relevant community detection problems which are structured by requirement.

Message passing for probabilistic models on networks with loops

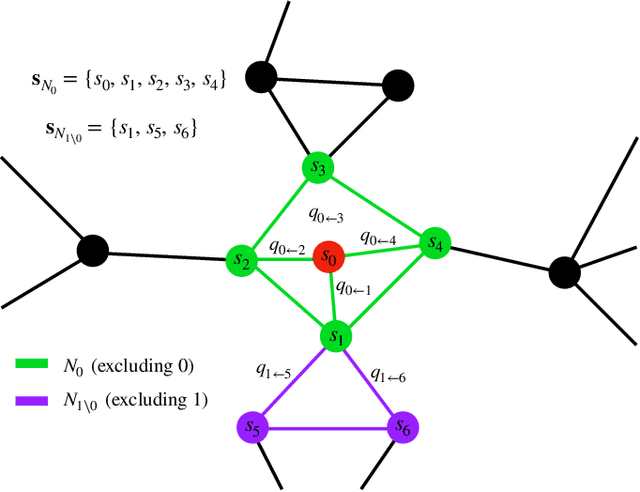
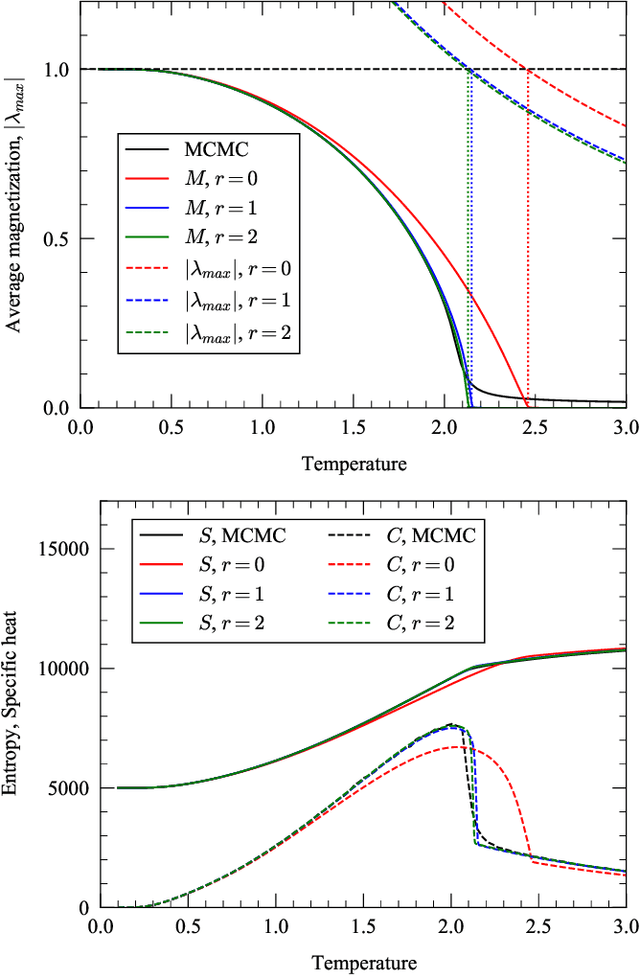
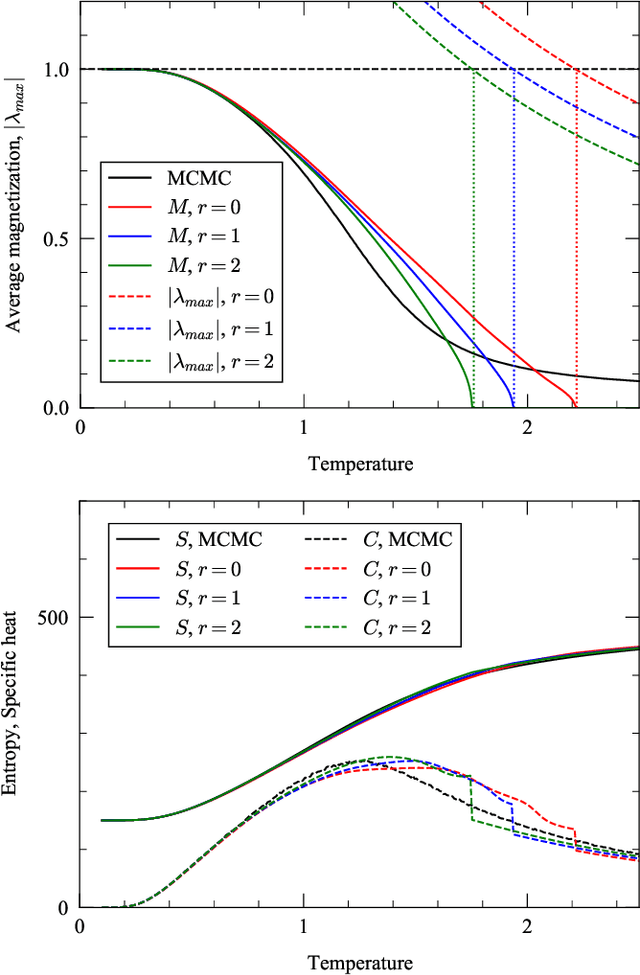
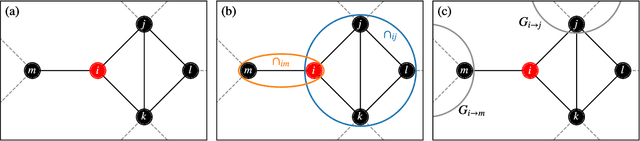
In this paper, we extend a recently proposed framework for message passing on "loopy" networks to the solution of probabilistic models. We derive a self-consistent set of message passing equations that allow for fast computation of probability distributions in systems that contain short loops, potentially with high density, as well as expressions for the entropy and partition function of such systems, which are notoriously difficult quantities to compute. Using the Ising model as an example, we show that our solutions are asymptotically exact on certain classes of networks with short loops and offer a good approximation on more general networks, improving significantly on results derived from standard belief propagation. We also discuss potential applications of our method to a variety of other problems.