Network reconstruction via the minimum description length principle

A fundamental problem associated with the task of network reconstruction from dynamical or behavioral data consists in determining the most appropriate model complexity in a manner that prevents overfitting, and produces an inferred network with a statistically justifiable number of edges. The status quo in this context is based on $L_{1}$ regularization combined with cross-validation. As we demonstrate, besides its high computational cost, this commonplace approach unnecessarily ties the promotion of sparsity with weight "shrinkage". This combination forces a trade-off between the bias introduced by shrinkage and the network sparsity, which often results in substantial overfitting even after cross-validation. In this work, we propose an alternative nonparametric regularization scheme based on hierarchical Bayesian inference and weight quantization, which does not rely on weight shrinkage to promote sparsity. Our approach follows the minimum description length (MDL) principle, and uncovers the weight distribution that allows for the most compression of the data, thus avoiding overfitting without requiring cross-validation. The latter property renders our approach substantially faster to employ, as it requires a single fit to the complete data. As a result, we have a principled and efficient inference scheme that can be used with a large variety of generative models, without requiring the number of edges to be known in advance. We also demonstrate that our scheme yields systematically increased accuracy in the reconstruction of both artificial and empirical networks. We highlight the use of our method with the reconstruction of interaction networks between microbial communities from large-scale abundance samples involving in the order of $10^{4}$ to $10^{5}$ species, and demonstrate how the inferred model can be used to predict the outcome of interventions in the system.

Scalable network reconstruction in subquadratic time

Network reconstruction consists in determining the unobserved pairwise couplings between $N$ nodes given only observational data on the resulting behavior that is conditioned on those couplings -- typically a time-series or independent samples from a graphical model. A major obstacle to the scalability of algorithms proposed for this problem is a seemingly unavoidable quadratic complexity of $O(N^2)$, corresponding to the requirement of each possible pairwise coupling being contemplated at least once, despite the fact that most networks of interest are sparse, with a number of non-zero couplings that is only $O(N)$. Here we present a general algorithm applicable to a broad range of reconstruction problems that achieves its result in subquadratic time, with a data-dependent complexity loosely upper bounded by $O(N^{3/2}\log N)$, but with a more typical log-linear complexity of $O(N\log^2N)$. Our algorithm relies on a stochastic second neighbor search that produces the best edge candidates with high probability, thus bypassing an exhaustive quadratic search. In practice, our algorithm achieves a performance that is many orders of magnitude faster than the quadratic baseline, allows for easy parallelization, and thus enables the reconstruction of networks with hundreds of thousands and even millions of nodes and edges.

Implicit models, latent compression, intrinsic biases, and cheap lunches in community detection

The task of community detection, which aims to partition a network into clusters of nodes to summarize its large-scale structure, has spawned the development of many competing algorithms with varying objectives. Some community detection methods are inferential, explicitly deriving the clustering objective through a probabilistic generative model, while other methods are descriptive, dividing a network according to an objective motivated by a particular application, making it challenging to compare these methods on the same scale. Here we present a solution to this problem that associates any community detection objective, inferential or descriptive, with its corresponding implicit network generative model. This allows us to compute the description length of a network and its partition under arbitrary objectives, providing a principled measure to compare the performance of different algorithms without the need for "ground truth" labels. Our approach also gives access to instances of the community detection problem that are optimal to any given algorithm, and in this way reveals intrinsic biases in popular descriptive methods, explaining their tendency to overfit. Using our framework, we compare a number of community detection methods on artificial networks, and on a corpus of over 500 structurally diverse empirical networks. We find that more expressive community detection methods exhibit consistently superior compression performance on structured data instances, without having degraded performance on a minority of situations where more specialized algorithms perform optimally. Our results undermine the implications of the "no free lunch" theorem for community detection, both conceptually and in practice, since it is confined to unstructured data instances, unlike relevant community detection problems which are structured by requirement.

Systematic assessment of the quality of fit of the stochastic block model for empirical networks

We perform a systematic analysis of the quality of fit of the stochastic block model (SBM) for 275 empirical networks spanning a wide range of domains and orders of size magnitude. We employ posterior predictive model checking as a criterion to assess the quality of fit, which involves comparing networks generated by the inferred model with the empirical network, according to a set of network descriptors. We observe that the SBM is capable of providing an accurate description for the majority of networks considered, but falls short of saturating all modeling requirements. In particular, networks possessing a large diameter and slow-mixing random walks tend to be badly described by the SBM. However, contrary to what is often assumed, networks with a high abundance of triangles can be well described by the SBM in many cases. We demonstrate that simple network descriptors can be used to evaluate whether or not the SBM can provide a sufficiently accurate representation, potentially pointing to possible model extensions that can systematically improve the expressiveness of this class of models.

Descriptive vs. inferential community detection: pitfalls, myths and half-truths

Community detection is one of the most important methodological fields of network science, and one which has attracted a significant amount of attention over the past decades. This area deals with the automated division of a network into fundamental building blocks, with the objective of providing a summary of its large-scale structure. Despite its importance and widespread adoption, there is a noticeable gap between what is considered the state-of-the-art and the methods that are actually used in practice in a variety of fields. Here we attempt to address this discrepancy by dividing existing methods according to whether they have a "descriptive" or an "inferential" goal. While descriptive methods find patterns in networks based on intuitive notions of community structure, inferential methods articulate a precise generative model, and attempt to fit it to data. In this way, they are able to provide insights into the mechanisms of network formation, and separate structure from randomness in a manner supported by statistical evidence. We review how employing descriptive methods with inferential aims is riddled with pitfalls and misleading answers, and thus should be in general avoided. We argue that inferential methods are more typically aligned with clearer scientific questions, yield more robust results, and should be in many cases preferred. We attempt to dispel some myths and half-truths often believed when community detection is employed in practice, in an effort to improve both the use of such methods as well as the interpretation of their results.

Multilayer Networks for Text Analysis with Multiple Data Types

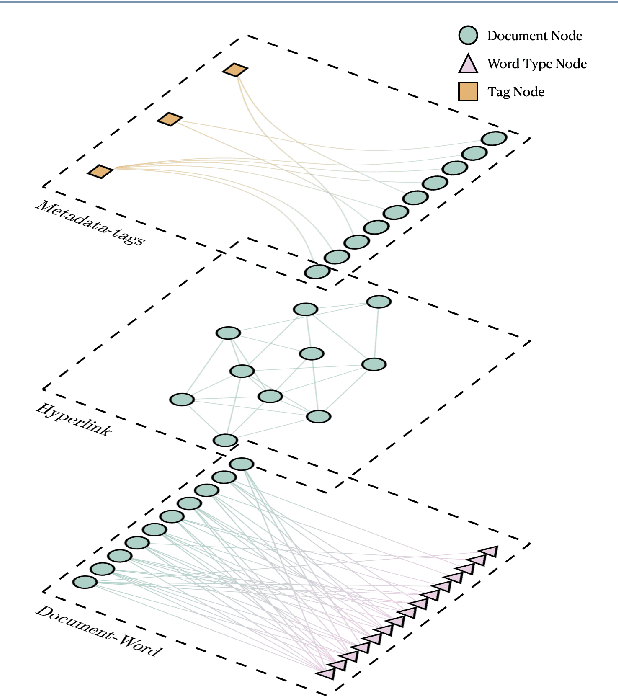
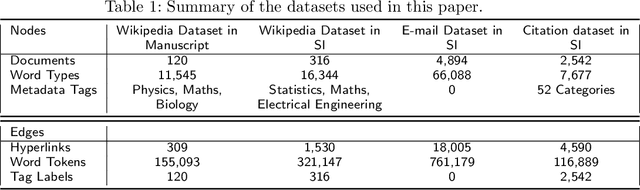
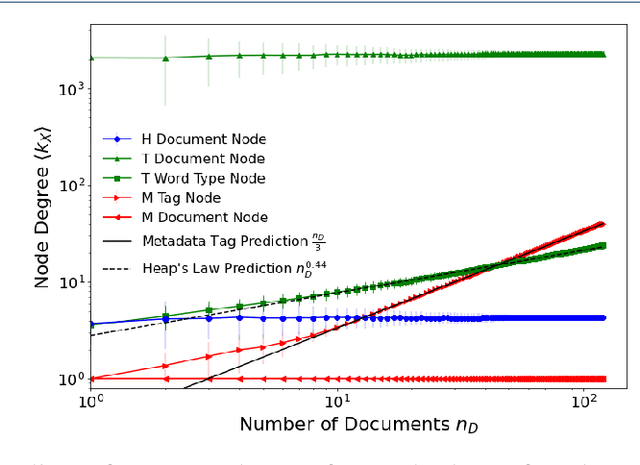
We are interested in the widespread problem of clustering documents and finding topics in large collections of written documents in the presence of metadata and hyperlinks. To tackle the challenge of accounting for these different types of datasets, we propose a novel framework based on Multilayer Networks and Stochastic Block Models. The main innovation of our approach over other techniques is that it applies the same non-parametric probabilistic framework to the different sources of datasets simultaneously. The key difference to other multilayer complex networks is the strong unbalance between the layers, with the average degree of different node types scaling differently with system size. We show that the latter observation is due to generic properties of text, such as Heaps' law, and strongly affects the inference of communities. We present and discuss the performance of our method in different datasets (hundreds of Wikipedia documents, thousands of scientific papers, and thousands of E-mails) showing that taking into account multiple types of information provides a more nuanced view on topic- and document-clusters and increases the ability to predict missing links.

Disentangling homophily, community structure and triadic closure in networks

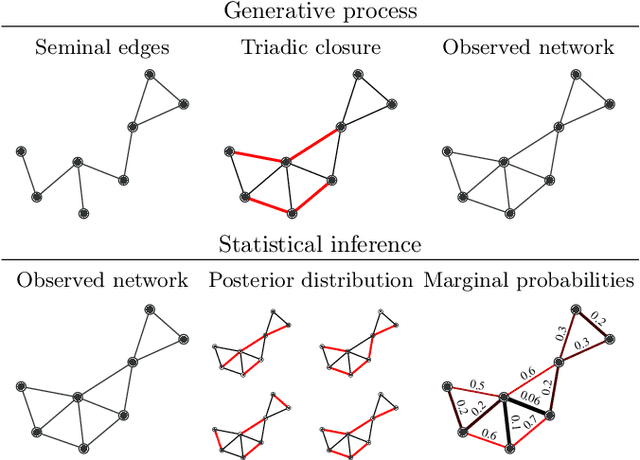
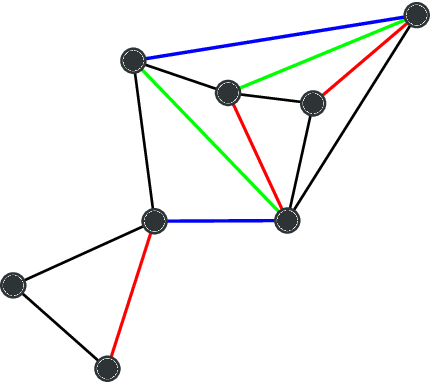
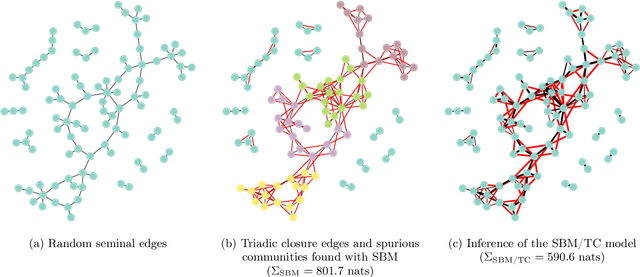
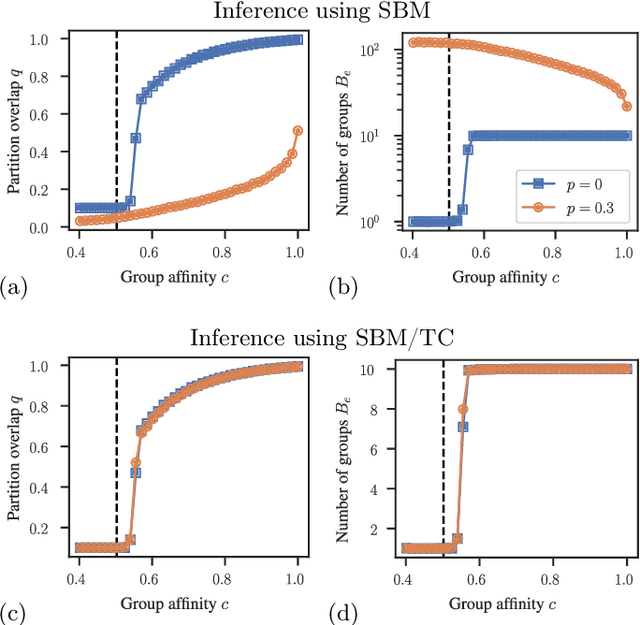
Network homophily, the tendency of similar nodes to be connected, and transitivity, the tendency of two nodes being connected if they share a common neighbor, are conflated properties in network analysis, since one mechanism can drive the other. Here we present a generative model and corresponding inference procedure that is capable of distinguishing between both mechanisms. Our approach is based on a variation of the stochastic block model (SBM) with the addition of triadic closure edges, and its inference can identify the most plausible mechanism responsible for the existence of every edge in the network, in addition to the underlying community structure itself. We show how the method can evade the detection of spurious communities caused solely by the formation of triangles in the network, and how it can improve the performance of link prediction when compared to the pure version of the SBM without triadic closure.

Hypergraph reconstruction from network data

Networks can describe the structure of a wide variety of complex systems by specifying how pairs of nodes interact. This choice of representation is flexible, but not necessarily appropriate when joint interactions between groups of nodes are needed to explain empirical phenomena. Networks remain the de facto standard, however, as relational datasets often fail to include higher-order interactions. Here, we introduce a Bayesian approach to reconstruct these missing higher-order interactions, from pairwise network data. Our method is based on the principle of parsimony and only includes higher-order structures when there is sufficient statistical evidence for them.

Statistical inference of assortative community structures

We develop a principled methodology to infer assortative communities in networks based on a nonparametric Bayesian formulation of the planted partition model. We show that this approach succeeds in finding statistically significant assortative modules in networks, unlike alternatives such as modularity maximization, which systematically overfits both in artificial as well as in empirical examples. In addition, we show that our method is not subject to a resolution limit, and can uncover an arbitrarily large number of communities, as long as there is statistical evidence for them. Our formulation is amenable to model selection procedures, which allow us to compare it to more general approaches based on the stochastic block model, and in this way reveal whether assortativity is in fact the dominating large-scale mixing pattern. We perform this comparison with several empirical networks, and identify numerous cases where the network's assortativity is exaggerated by traditional community detection methods, and we show how a more faithful degree of assortativity can be identified.

Revealing consensus and dissensus between network partitions

Community detection methods attempt to divide a network into groups of nodes that share similar properties, thus revealing its large-scale structure. A major challenge when employing such methods is that they are often degenerate, typically yielding a complex landscape of competing answers. As an attempt to extract understanding from a population of alternative solutions, many methods exist to establish a consensus among them in the form of a single partition "point estimate" that summarizes the whole distribution. Here we show that it is in general not possible to obtain a consistent answer from such point estimates when the underlying distribution is too heterogeneous. As an alternative, we provide a comprehensive set of methods designed to characterize and summarize complex populations of partitions in a manner that captures not only the existing consensus, but also the dissensus between elements of the population. Our approach is able to model mixed populations of partitions where multiple consensuses can coexist, representing different competing hypotheses for the network structure. We also show how our methods can be used to compare pairs of partitions, how they can be generalized to hierarchical divisions, and be used to perform statistical model selection between competing hypotheses.