Symmetry-driven embedding of networks in hyperbolic space

Hyperbolic models can reproduce the heavy-tailed degree distribution, high clustering, and hierarchical structure of empirical networks. Current algorithms for finding the hyperbolic coordinates of networks, however, do not quantify uncertainty in the inferred coordinates. We present BIGUE, a Markov chain Monte Carlo (MCMC) algorithm that samples the posterior distribution of a Bayesian hyperbolic random graph model. We show that combining random walk and random cluster transformations significantly improves mixing compared to the commonly used and state-of-the-art dynamic Hamiltonian Monte Carlo algorithm. Using this algorithm, we also provide evidence that the posterior distribution cannot be approximated by a multivariate normal distribution, thereby justifying the use of MCMC to quantify the uncertainty of the inferred parameters.

Complex contagions can outperform simple contagions for network reconstruction with dense networks or saturated dynamics

Network scientists often use complex dynamic processes to describe network contagions, but tools for fitting contagion models typically assume simple dynamics. Here, we address this gap by developing a nonparametric method to reconstruct a network and dynamics from a series of node states, using a model that breaks the dichotomy between simple pairwise and complex neighborhood-based contagions. We then show that a network is more easily reconstructed when observed through the lens of complex contagions if it is dense or the dynamic saturates, and that simple contagions are better otherwise.

Exact and rapid linear clustering of networks with dynamic programming

We study the problem of clustering networks whose nodes have imputed or physical positions in a single dimension, such as prestige hierarchies or the similarity dimension of hyperbolic embeddings. Existing algorithms, such as the critical gap method and other greedy strategies, only offer approximate solutions. Here, we introduce a dynamic programming approach that returns provably optimal solutions in polynomial time -- O(n^2) steps -- for a broad class of clustering objectives. We demonstrate the algorithm through applications to synthetic and empirical networks, and show that it outperforms existing heuristics by a significant margin, with a similar execution time.

Impact and dynamics of hate and counter speech online

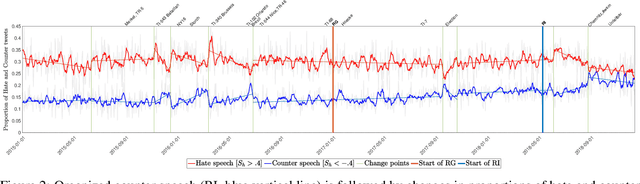
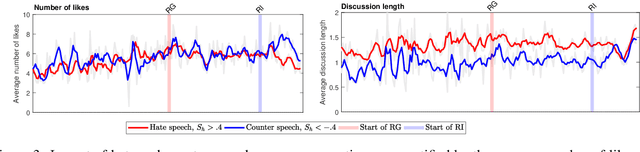
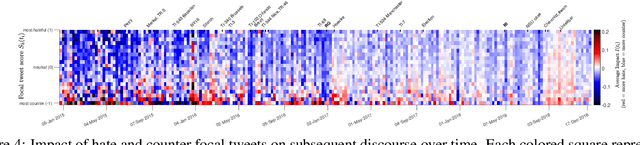
Citizen-generated counter speech is a promising way to fight hate speech and promote peaceful, non-polarized discourse. However, there is a lack of large-scale longitudinal studies of its effectiveness for reducing hate speech. We investigate the effectiveness of counter speech using several different macro- and micro-level measures of over 180,000 political conversations that took place on German Twitter over four years. We report on the dynamic interactions of hate and counter speech over time and provide insights into whether, as in `classic' bullying situations, organized efforts are more effective than independent individuals in steering online discourse. Taken together, our results build a multifaceted picture of the dynamics of hate and counter speech online. They suggest that organized hate speech produced changes in the public discourse. Counter speech, especially when organized, could help in curbing hate speech in online discussions.

Hypergraph reconstruction from network data

Networks can describe the structure of a wide variety of complex systems by specifying how pairs of nodes interact. This choice of representation is flexible, but not necessarily appropriate when joint interactions between groups of nodes are needed to explain empirical phenomena. Networks remain the de facto standard, however, as relational datasets often fail to include higher-order interactions. Here, we introduce a Bayesian approach to reconstruct these missing higher-order interactions, from pairwise network data. Our method is based on the principle of parsimony and only includes higher-order structures when there is sufficient statistical evidence for them.

Countering hate on social media: Large scale classification of hate and counter speech

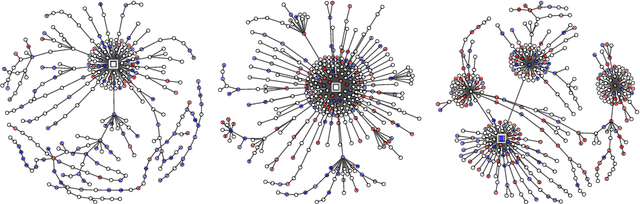
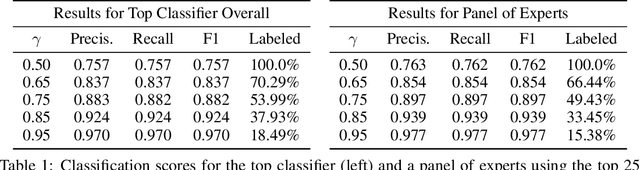
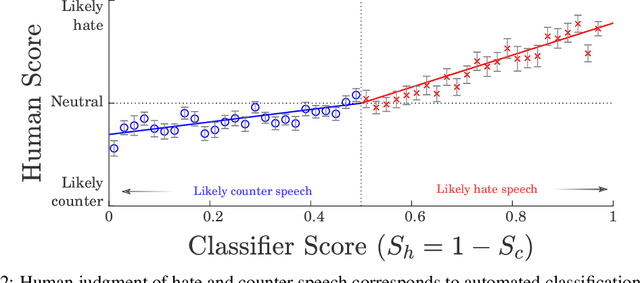
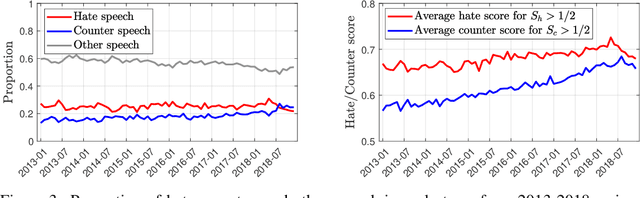
Hateful rhetoric is plaguing online discourse, fostering extreme societal movements and possibly giving rise to real-world violence. A potential solution to this growing global problem is citizen-generated counter speech where citizens actively engage in hate-filled conversations to attempt to restore civil non-polarized discourse. However, its actual effectiveness in curbing the spread of hatred is unknown and hard to quantify. One major obstacle to researching this question is a lack of large labeled data sets for training automated classifiers to identify counter speech. Here we made use of a unique situation in Germany where self-labeling groups engaged in organized online hate and counter speech. We used an ensemble learning algorithm which pairs a variety of paragraph embeddings with regularized logistic regression functions to classify both hate and counter speech in a corpus of millions of relevant tweets from these two groups. Our pipeline achieved macro F1 scores on out of sample balanced test sets ranging from 0.76 to 0.97---accuracy in line and even exceeding the state of the art. On thousands of tweets, we used crowdsourcing to verify that the judgments made by the classifier are in close alignment with human judgment. We then used the classifier to discover hate and counter speech in more than 135,000 fully-resolved Twitter conversations occurring from 2013 to 2018 and study their frequency and interaction. Altogether, our results highlight the potential of automated methods to evaluate the impact of coordinated counter speech in stabilizing conversations on social media.

Universality of the stochastic block model

Mesoscopic pattern extraction (MPE) is the problem of finding a partition of the nodes of a complex network that maximizes some objective function. Many well-known network inference problems fall in this category, including, for instance, community detection, core-periphery identification, and imperfect graph coloring. In this paper, we show that the most popular algorithms designed to solve MPE problems can in fact be understood as special cases of the maximum likelihood formulation of the stochastic block model (SBM), or one of its direct generalizations. These equivalence relations show that the SBM is nearly universal with respect to MPE problems.

Network archaeology: phase transition in the recoverability of network history

Network growth processes can be understood as generative models of the structure and history of complex networks. This point of view naturally leads to the problem of network archaeology: Reconstructing all the past states of a network from its structure---a difficult permutation inference problem. In this paper, we introduce a Bayesian formulation of network archaeology, with a generalization of preferential attachment as our generative mechanism. We develop a sequential importance sampling algorithm to evaluate the posterior averages of this model, as well as an efficient heuristic that uncovers the history of a network in linear time. We use these methods to identify and characterize a phase transition in the quality of the reconstructed history, when they are applied to artificial networks generated by the model itself. Despite the existence of a no-recovery phase, we find that non-trivial inference is possible in a large portion of the parameter space as well as on empirical data.