A theoretical framework for reservoir computing on networks of organic electrochemical transistors

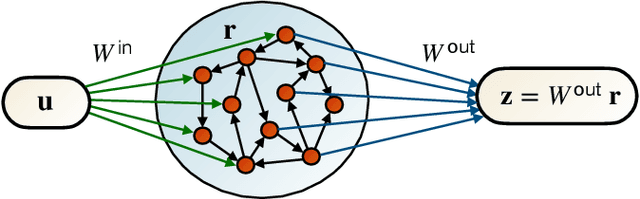
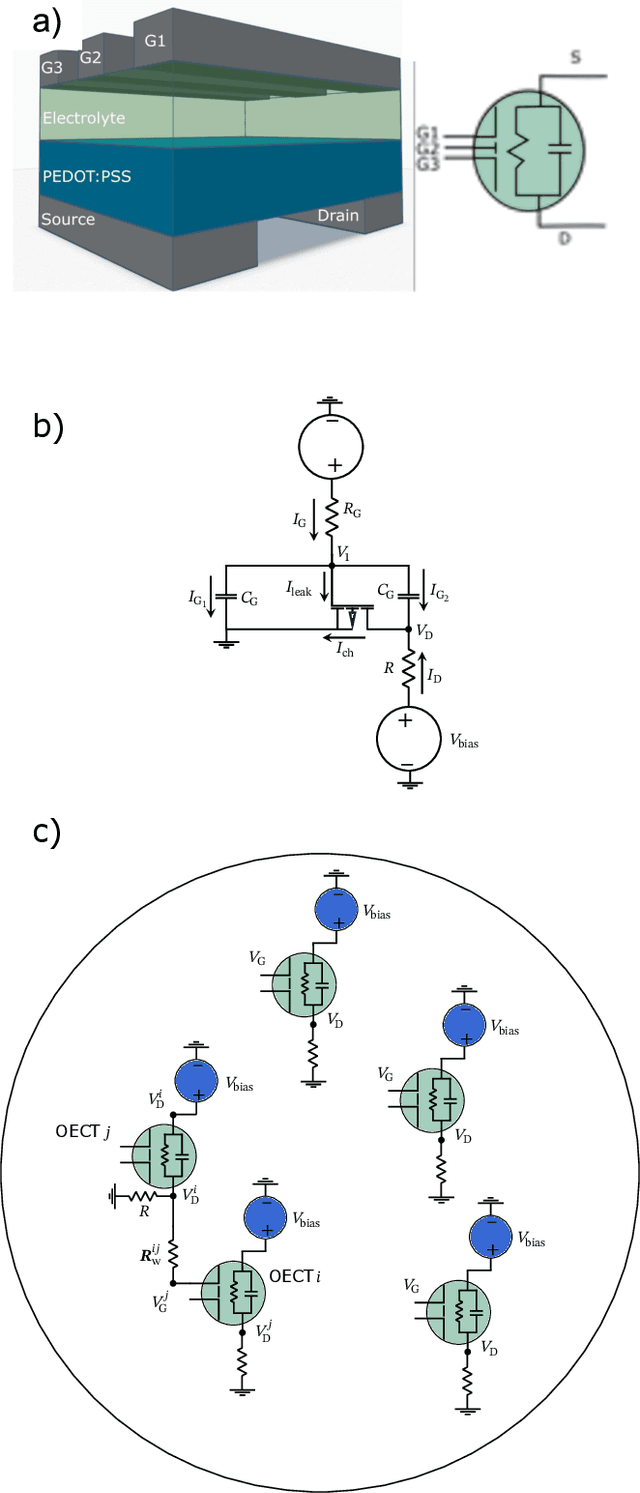
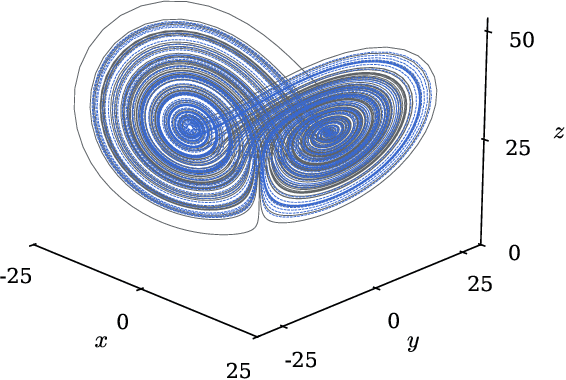
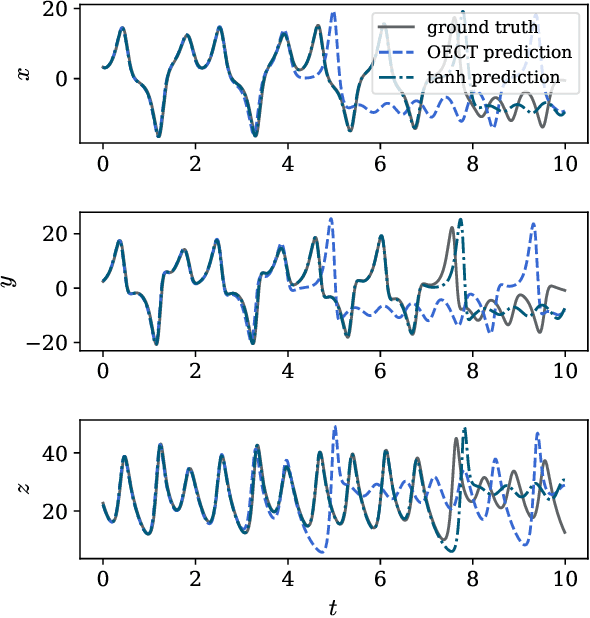
Efficient and accurate prediction of physical systems is important even when the rules of those systems cannot be easily learned. Reservoir computing, a type of recurrent neural network with fixed nonlinear units, is one such prediction method and is valued for its ease of training. Organic electrochemical transistors (OECTs) are physical devices with nonlinear transient properties that can be used as the nonlinear units of a reservoir computer. We present a theoretical framework for simulating reservoir computers using OECTs as the non-linear units as a test bed for designing physical reservoir computers. We present a proof of concept demonstrating that such an implementation can accurately predict the Lorenz attractor with comparable performance to standard reservoir computer implementations. We explore the effect of operating parameters and find that the prediction performance strongly depends on the pinch-off voltage of the OECTs.

Complex contagions can outperform simple contagions for network reconstruction with dense networks or saturated dynamics

Network scientists often use complex dynamic processes to describe network contagions, but tools for fitting contagion models typically assume simple dynamics. Here, we address this gap by developing a nonparametric method to reconstruct a network and dynamics from a series of node states, using a model that breaks the dichotomy between simple pairwise and complex neighborhood-based contagions. We then show that a network is more easily reconstructed when observed through the lens of complex contagions if it is dense or the dynamic saturates, and that simple contagions are better otherwise.