A theoretical framework for reservoir computing on networks of organic electrochemical transistors

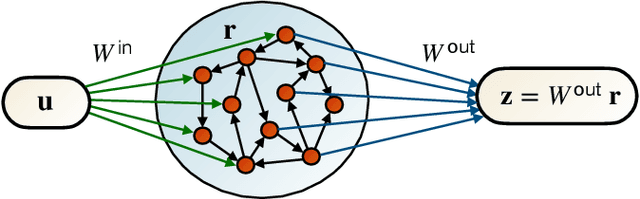
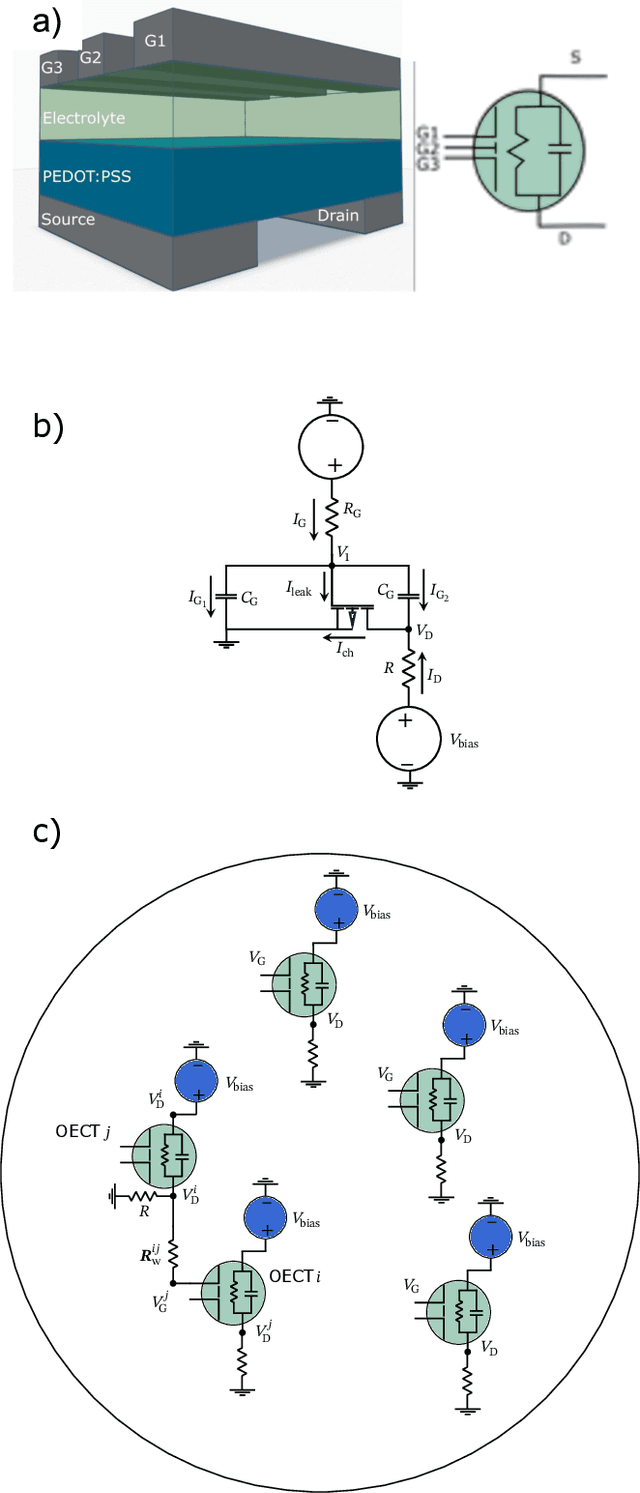
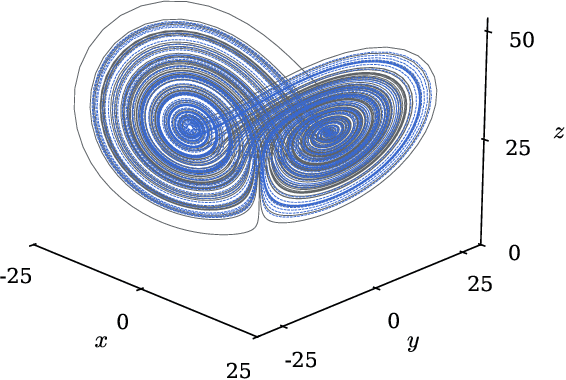
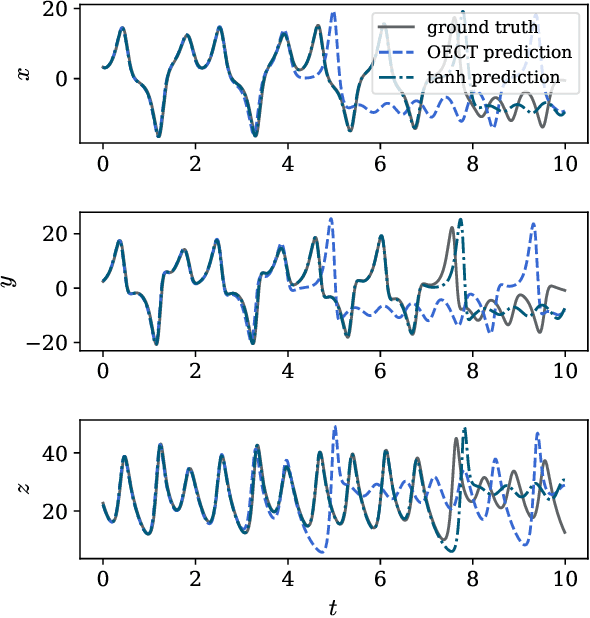
Efficient and accurate prediction of physical systems is important even when the rules of those systems cannot be easily learned. Reservoir computing, a type of recurrent neural network with fixed nonlinear units, is one such prediction method and is valued for its ease of training. Organic electrochemical transistors (OECTs) are physical devices with nonlinear transient properties that can be used as the nonlinear units of a reservoir computer. We present a theoretical framework for simulating reservoir computers using OECTs as the non-linear units as a test bed for designing physical reservoir computers. We present a proof of concept demonstrating that such an implementation can accurately predict the Lorenz attractor with comparable performance to standard reservoir computer implementations. We explore the effect of operating parameters and find that the prediction performance strongly depends on the pinch-off voltage of the OECTs.

Tuning the activation function to optimize the forecast horizon of a reservoir computer

Reservoir computing is a machine learning framework where the readouts from a nonlinear system (the reservoir) are trained so that the output from the reservoir, when forced with an input signal, reproduces a desired output signal. A common implementation of reservoir computers is to use a recurrent neural network as the reservoir. The design of this network can have significant effects on the performance of the reservoir computer. In this paper we study the effect of the node activation function on the ability of reservoir computers to learn and predict chaotic time series. We find that the Forecast Horizon (FH), the time during which the reservoir's predictions remain accurate, can vary by an order of magnitude across a set of 16 activation functions used in machine learning. By using different functions from this set, and by modifying their parameters, we explore whether the entropy of node activation levels or the curvature of the activation functions determine the predictive ability of the reservoirs. We find that the FH is low when the activation function is used in a region where it has low curvature, and a positive correlation between curvature and FH. For the activation functions studied we find that the largest FH generally occurs at intermediate levels of the entropy of node activation levels. Our results show that the performance of reservoir computers is very sensitive to the activation function shape. Therefore, modifying this shape in hyperparameter optimization algorithms can lead to improvements in reservoir computer performance.

Detecting disturbances in network-coupled dynamical systems with machine learning

Identifying disturbances in network-coupled dynamical systems without knowledge of the disturbances or underlying dynamics is a problem with a wide range of applications. For example, one might want to know which nodes in the network are being disturbed and identify the type of disturbance. Here we present a model-free method based on machine learning to identify such unknown disturbances based only on prior observations of the system when forced by a known training function. We find that this method is able to identify the locations and properties of many different types of unknown disturbances using a variety of known forcing functions. We illustrate our results both with linear and nonlinear disturbances using food web and neuronal activity models. Finally, we discuss how to scale our method to large networks.

Suppressing unknown disturbances to dynamical systems using machine learning

Identifying and suppressing unknown disturbances to dynamical systems is a problem with applications in many different fields. In this Letter, we present a model-free method to identify and suppress an unknown disturbance to an unknown system based only on previous observations of the system under the influence of a known forcing function. We find that, under very mild restrictions on the training function, our method is able to robustly identify and suppress a large class of unknown disturbances. We illustrate our scheme with an example where a chaotic disturbance to the Lorenz system is identified and suppressed.

Using Machine Learning to Assess Short Term Causal Dependence and Infer Network Links

We introduce and test a general machine-learning-based technique for the inference of short term causal dependence between state variables of an unknown dynamical system from time series measurements of its state variables. Our technique leverages the results of a machine learning process for short time prediction to achieve our goal. The basic idea is to use the machine learning to estimate the elements of the Jacobian matrix of the dynamical flow along an orbit. The type of machine learning that we employ is reservoir computing. We present numerical tests on link inference of a network of interacting dynamical nodes. It is seen that dynamical noise can greatly enhance the effectiveness of our technique, while observational noise degrades the effectiveness. We believe that the competition between these two opposing types of noise will be the key factor determining the success of causal inference in many of the most important application situations.