Edward Ott
Tailored Forecasting from Short Time Series via Meta-learning
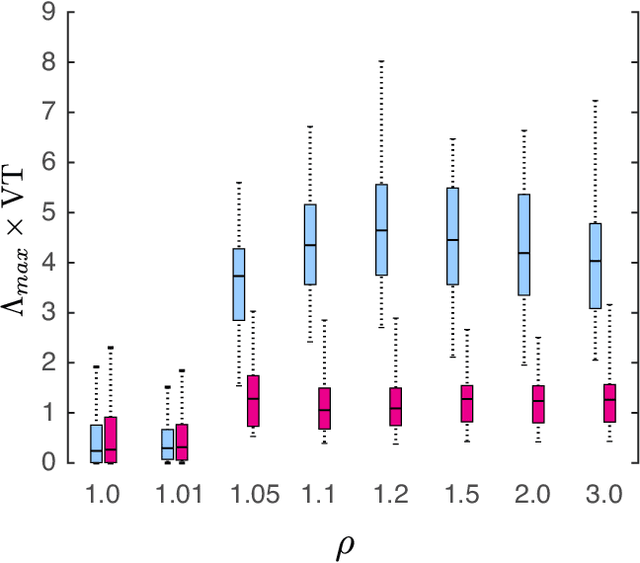
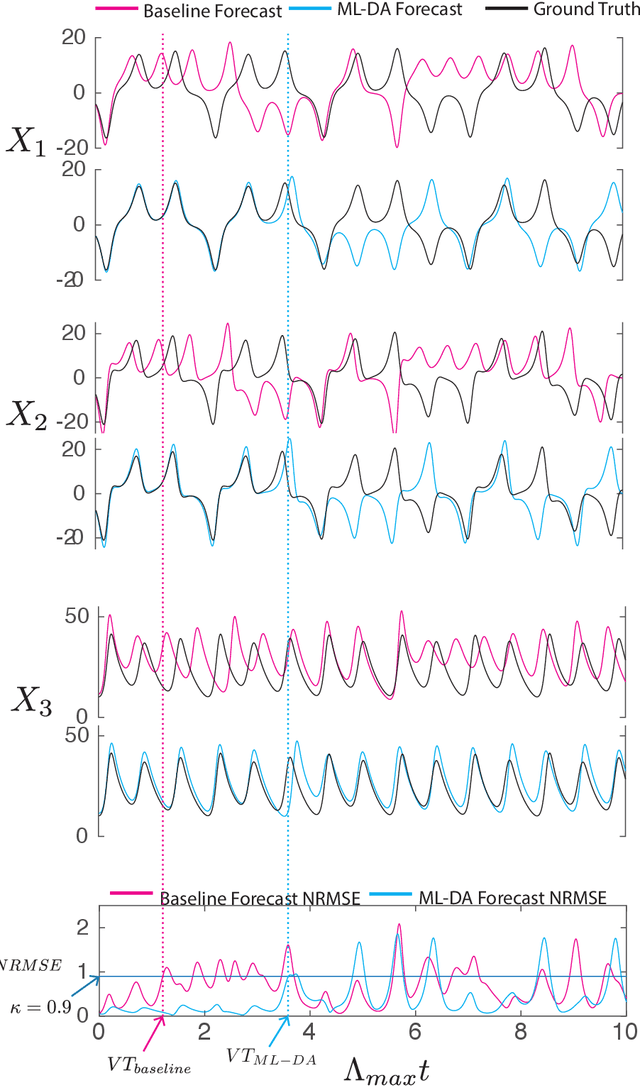
Jan 27, 2025Abstract:Machine learning (ML) models can be effective for forecasting the dynamics of unknown systems from time-series data, but they often require large amounts of data and struggle to generalize across systems with varying dynamics. Combined, these issues make forecasting from short time series particularly challenging. To address this problem, we introduce Meta-learning for Tailored Forecasting from Related Time Series (METAFORS), which uses related systems with longer time-series data to supplement limited data from the system of interest. By leveraging a library of models trained on related systems, METAFORS builds tailored models to forecast system evolution with limited data. Using a reservoir computing implementation and testing on simulated chaotic systems, we demonstrate METAFORS' ability to predict both short-term dynamics and long-term statistics, even when test and related systems exhibit significantly different behaviors and the available data are scarce, highlighting its robustness and versatility in data-limited scenarios.
Exploring the Potential of Hybrid Machine-Learning/Physics-Based Modeling for Atmospheric/Oceanic Prediction Beyond the Medium Range
May 29, 2024Abstract:This paper explores the potential of a hybrid modeling approach that combines machine learning (ML) with conventional physics-based modeling for weather prediction beyond the medium range. It extends the work of Arcomano et al. (2022), which tested the approach for short- and medium-range weather prediction, and the work of Arcomano et al. (2023), which investigated its potential for climate modeling. The hybrid model used for the forecast experiments of the paper is based on the low-resolution, simplified parameterization atmospheric general circulation model (AGCM) SPEEDY. In addition to the hybridized prognostic variables of SPEEDY, the current version of the model has three purely ML-based prognostic variables. One of these is 6~h cumulative precipitation, another is the sea surface temperature, while the third is the heat content of the top 300 m deep layer of the ocean. The model has skill in predicting the El Ni\~no cycle and its global teleconnections with precipitation for 3-7 months depending on the season. The model captures equatorial variability of the precipitation associated with Kelvin and Rossby waves and MJO. Predictions of the precipitation in the equatorial region have skill for 15 days in the East Pacific and 11.5 days in the West Pacific. Though the model has low spatial resolution, for these tasks it has prediction skill comparable to what has been published for high-resolution, purely physics-based, conventional operational forecast models.
Stabilizing Machine Learning Prediction of Dynamics: Noise and Noise-inspired Regularization
Nov 09, 2022Abstract:Recent work has shown that machine learning (ML) models can be trained to accurately forecast the dynamics of unknown chaotic dynamical systems. Such ML models can be used to produce both short-term predictions of the state evolution and long-term predictions of the statistical patterns of the dynamics (``climate''). Both of these tasks can be accomplished by employing a feedback loop, whereby the model is trained to predict forward one time step, then the trained model is iterated for multiple time steps with its output used as the input. In the absence of mitigating techniques, however, this technique can result in artificially rapid error growth, leading to inaccurate predictions and/or climate instability. In this article, we systematically examine the technique of adding noise to the ML model input during training as a means to promote stability and improve prediction accuracy. Furthermore, we introduce Linearized Multi-Noise Training (LMNT), a regularization technique that deterministically approximates the effect of many small, independent noise realizations added to the model input during training. Our case study uses reservoir computing, a machine-learning method using recurrent neural networks, to predict the spatiotemporal chaotic Kuramoto-Sivashinsky equation. We find that reservoir computers trained with noise or with LMNT produce climate predictions that appear to be indefinitely stable and have a climate very similar to the true system, while reservoir computers trained without regularization are unstable. Compared with other types of regularization that yield stability in some cases, we find that both short-term and climate predictions from reservoir computers trained with noise or with LMNT are substantially more accurate. Finally, we show that the deterministic aspect of our LMNT regularization facilitates fast hyperparameter tuning when compared to training with noise.
Using Machine Learning to Anticipate Tipping Points and Extrapolate to Post-Tipping Dynamics of Non-Stationary Dynamical Systems
Jul 01, 2022

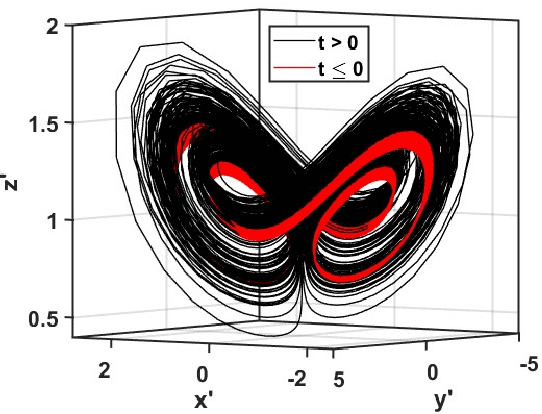
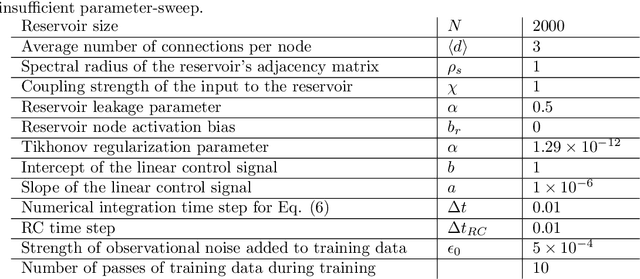
Abstract:In this paper we consider the machine learning (ML) task of predicting tipping point transitions and long-term post-tipping-point behavior associated with the time evolution of an unknown (or partially unknown), non-stationary, potentially noisy and chaotic, dynamical system. We focus on the particularly challenging situation where the past dynamical state time series that is available for ML training predominantly lies in a restricted region of the state space, while the behavior to be predicted evolves on a larger state space set not fully observed by the ML model during training. In this situation, it is required that the ML prediction system have the ability to extrapolate to different dynamics past that which is observed during training. We investigate the extent to which ML methods are capable of accomplishing useful results for this task, as well as conditions under which they fail. In general, we found that the ML methods were surprisingly effective even in situations that were extremely challenging, but do (as one would expect) fail when ``too much" extrapolation is required. For the latter case, we investigate the effectiveness of combining the ML approach with conventional modeling based on scientific knowledge, thus forming a hybrid prediction system which we find can enable useful prediction even when its ML-based and knowledge-based components fail when acting alone. We also found that achieving useful results may require using very carefully selected ML hyperparameters and we propose a hyperparameter optimization strategy to address this problem. The main conclusion of this paper is that ML-based approaches are promising tools for predicting the behavior of non-stationary dynamical systems even in the case where the future evolution (perhaps due to the crossing of a tipping point) includes dynamics on a set outside of that explored by the training data.
Short-wavelength Reverberant Wave Systems for Physical Realization of Reservoir Computing
Apr 13, 2022



Abstract:Machine learning (ML) has found widespread application over a broad range of important tasks. To enhance ML performance, researchers have investigated computational architectures whose physical implementations promise compactness, high-speed execution, physical robustness, and low energy cost. Here, we experimentally demonstrate an approach that uses the high sensitivity of reverberant short wavelength waves for physical realization and enhancement of computational power of a type of ML known as reservoir computing (RC). The potential computation power of RC systems increases with their effective size. We here exploit the intrinsic property of short wavelength reverberant wave sensitivity to perturbations to expand the effective size of the RC system by means of spatial and spectral perturbations. Working in the microwave regime, this scheme is tested experimentally on different ML tasks. Our results indicate the general applicability of reverberant wave-based implementations of RC and of our effective reservoir size expansion technique
Parallel Machine Learning for Forecasting the Dynamics of Complex Networks
Aug 27, 2021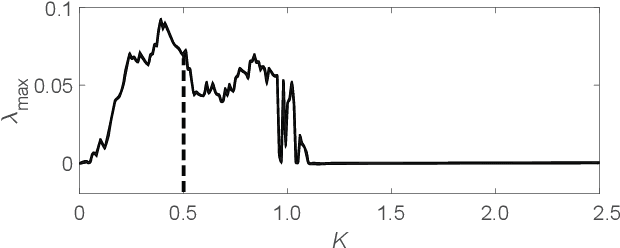
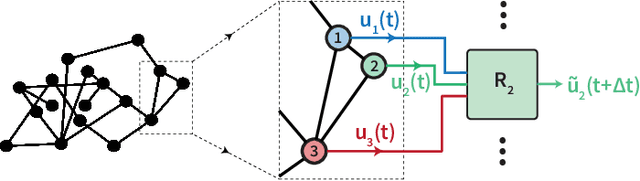
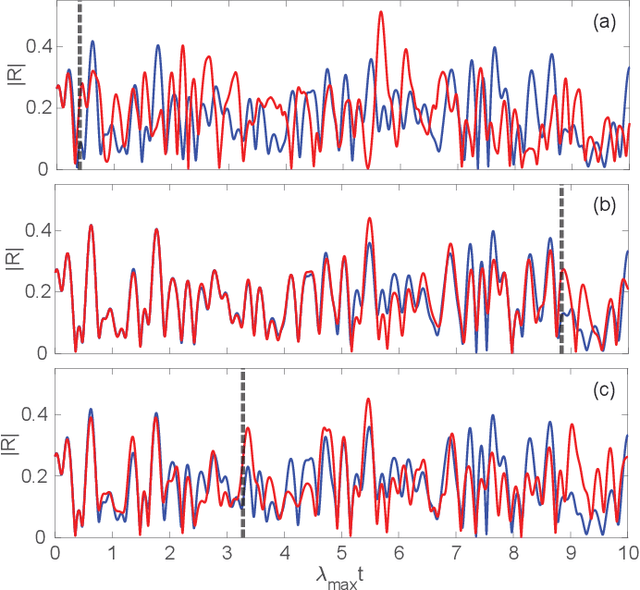
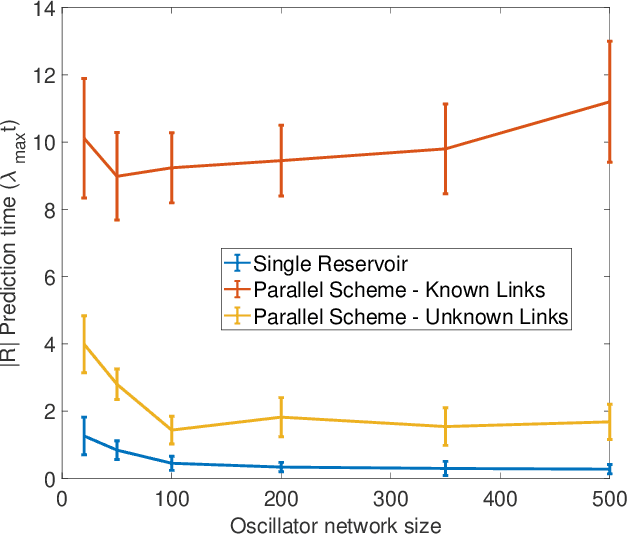
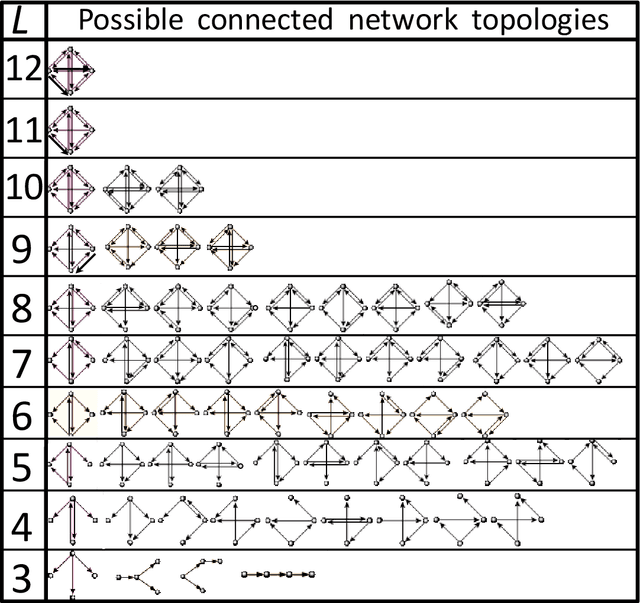
Abstract:Forecasting the dynamics of large complex networks from previous time-series data is important in a wide range of contexts. Here we present a machine learning scheme for this task using a parallel architecture that mimics the topology of the network of interest. We demonstrate the utility and scalability of our method implemented using reservoir computing on a chaotic network of oscillators. Two levels of prior knowledge are considered: (i) the network links are known; and (ii) the network links are unknown and inferred via a data-driven approach to approximately optimize prediction.
Using Data Assimilation to Train a Hybrid Forecast System that Combines Machine-Learning and Knowledge-Based Components
Feb 15, 2021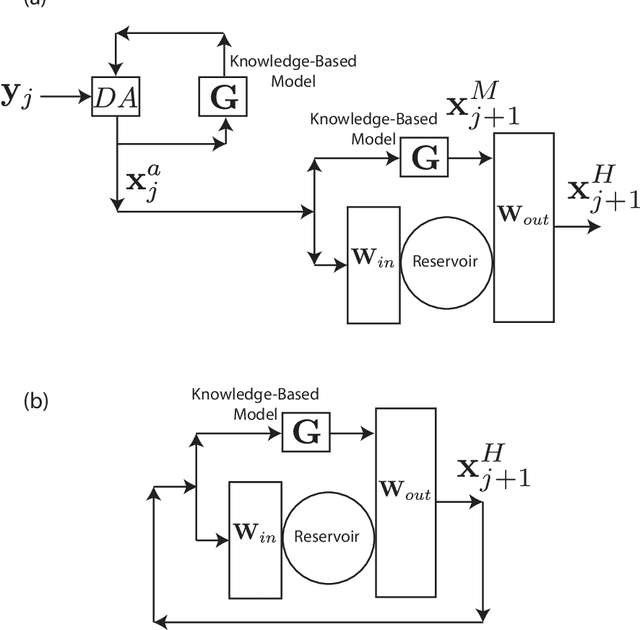
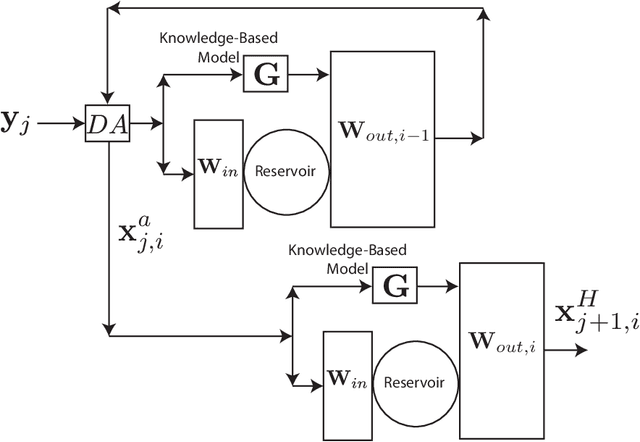
Abstract:We consider the problem of data-assisted forecasting of chaotic dynamical systems when the available data is in the form of noisy partial measurements of the past and present state of the dynamical system. Recently there have been several promising data-driven approaches to forecasting of chaotic dynamical systems using machine learning. Particularly promising among these are hybrid approaches that combine machine learning with a knowledge-based model, where a machine-learning technique is used to correct the imperfections in the knowledge-based model. Such imperfections may be due to incomplete understanding and/or limited resolution of the physical processes in the underlying dynamical system, e.g., the atmosphere or the ocean. Previously proposed data-driven forecasting approaches tend to require, for training, measurements of all the variables that are intended to be forecast. We describe a way to relax this assumption by combining data assimilation with machine learning. We demonstrate this technique using the Ensemble Transform Kalman Filter (ETKF) to assimilate synthetic data for the 3-variable Lorenz system and for the Kuramoto-Sivashinsky system, simulating model error in each case by a misspecified parameter value. We show that by using partial measurements of the state of the dynamical system, we can train a machine learning model to improve predictions made by an imperfect knowledge-based model.
Link inference of noisy delay-coupled networks: Machine learning and opto-electronic experimental tests
Oct 29, 2020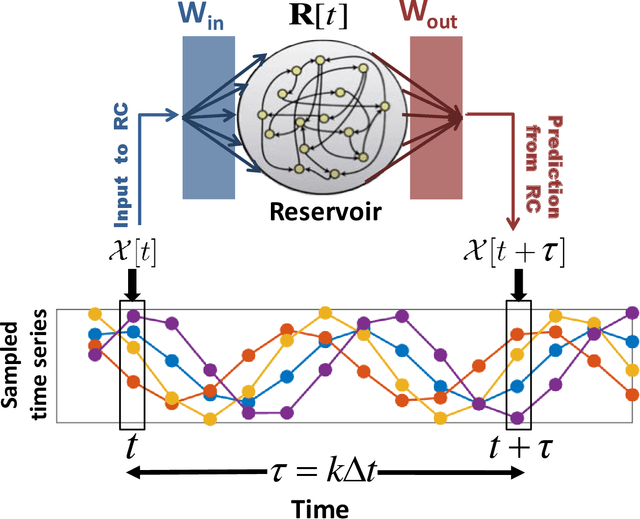

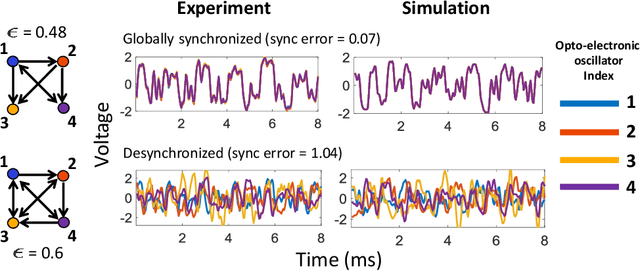
Abstract:We devise a machine learning technique to solve the general problem of inferring network links that have time-delays. The goal is to do this purely from time-series data of the network nodal states. This task has applications in fields ranging from applied physics and engineering to neuroscience and biology. To achieve this, we first train a type of machine learning system known as reservoir computing to mimic the dynamics of the unknown network. We formulate and test a technique that uses the trained parameters of the reservoir system output layer to deduce an estimate of the unknown network structure. Our technique, by its nature, is non-invasive, but is motivated by the widely-used invasive network inference method whereby the responses to active perturbations applied to the network are observed and employed to infer network links (e.g., knocking down genes to infer gene regulatory networks). We test this technique on experimental and simulated data from delay-coupled opto-electronic oscillator networks. We show that the technique often yields very good results particularly if the system does not exhibit synchrony. We also find that the presence of dynamical noise can strikingly enhance the accuracy and ability of our technique, especially in networks that exhibit synchrony.
Combining Machine Learning with Knowledge-Based Modeling for Scalable Forecasting and Subgrid-Scale Closure of Large, Complex, Spatiotemporal Systems
Feb 10, 2020
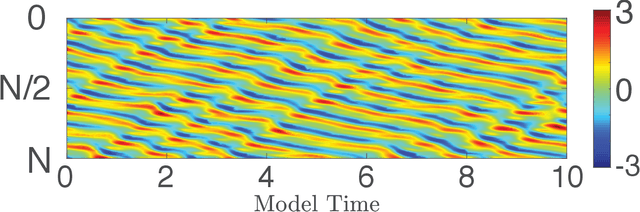
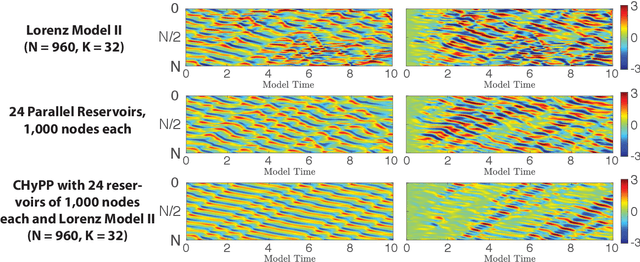
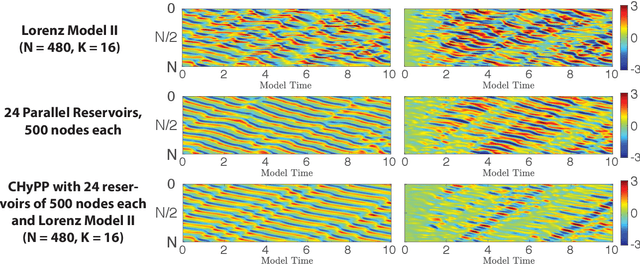
Abstract:We consider the commonly encountered situation (e.g., in weather forecasting) where the goal is to predict the time evolution of a large, spatiotemporally chaotic dynamical system when we have access to both time series data of previous system states and an imperfect model of the full system dynamics. Specifically, we attempt to utilize machine learning as the essential tool for integrating the use of past data into predictions. In order to facilitate scalability to the common scenario of interest where the spatiotemporally chaotic system is very large and complex, we propose combining two approaches:(i) a parallel machine learning prediction scheme; and (ii) a hybrid technique, for a composite prediction system composed of a knowledge-based component and a machine-learning-based component. We demonstrate that not only can this method combining (i) and (ii) be scaled to give excellent performance for very large systems, but also that the length of time series data needed to train our multiple, parallel machine learning components is dramatically less than that necessary without parallelization. Furthermore, considering cases where computational realization of the knowledge-based component does not resolve subgrid-scale processes, our scheme is able to use training data to incorporate the effect of the unresolved short-scale dynamics upon the resolved longer-scale dynamics ("subgrid-scale closure").
Using Machine Learning to Assess Short Term Causal Dependence and Infer Network Links
Dec 05, 2019



Abstract:We introduce and test a general machine-learning-based technique for the inference of short term causal dependence between state variables of an unknown dynamical system from time series measurements of its state variables. Our technique leverages the results of a machine learning process for short time prediction to achieve our goal. The basic idea is to use the machine learning to estimate the elements of the Jacobian matrix of the dynamical flow along an orbit. The type of machine learning that we employ is reservoir computing. We present numerical tests on link inference of a network of interacting dynamical nodes. It is seen that dynamical noise can greatly enhance the effectiveness of our technique, while observational noise degrades the effectiveness. We believe that the competition between these two opposing types of noise will be the key factor determining the success of causal inference in many of the most important application situations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge