A Meta-learning Approach to Reservoir Computing: Time Series Prediction with Limited Data

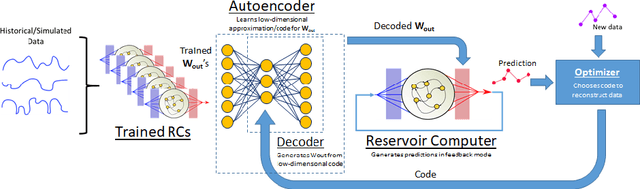
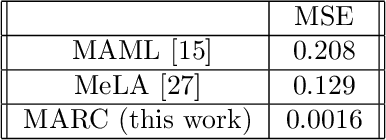
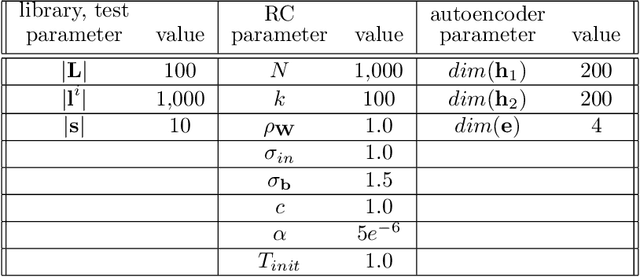
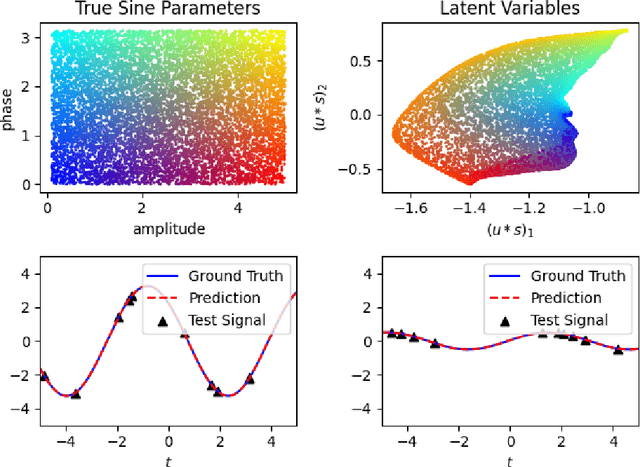
Recent research has established the effectiveness of machine learning for data-driven prediction of the future evolution of unknown dynamical systems, including chaotic systems. However, these approaches require large amounts of measured time series data from the process to be predicted. When only limited data is available, forecasters are forced to impose significant model structure that may or may not accurately represent the process of interest. In this work, we present a Meta-learning Approach to Reservoir Computing (MARC), a data-driven approach to automatically extract an appropriate model structure from experimentally observed "related" processes that can be used to vastly reduce the amount of data required to successfully train a predictive model. We demonstrate our approach on a simple benchmark problem, where it beats the state of the art meta-learning techniques, as well as a challenging chaotic problem.

Model-Free Control of Dynamical Systems with Deep Reservoir Computing

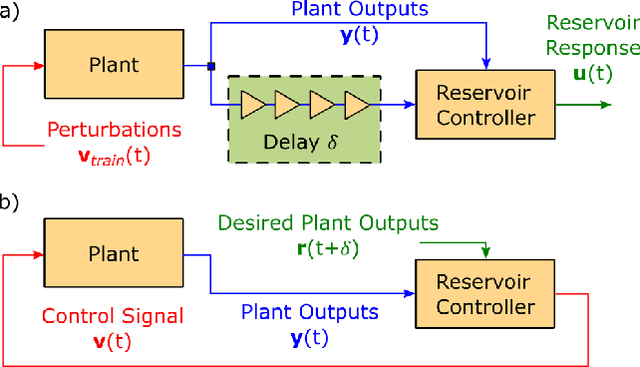
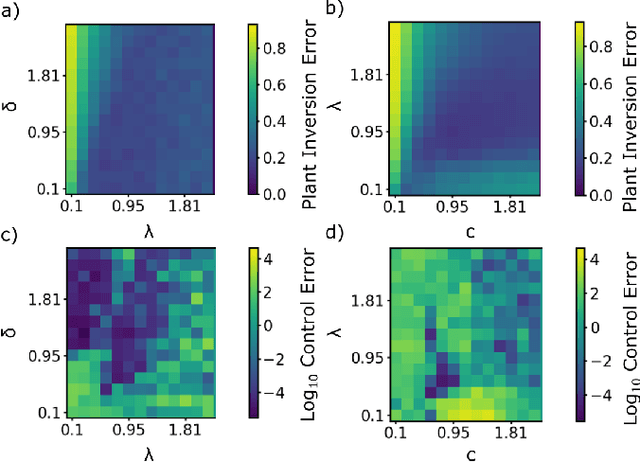
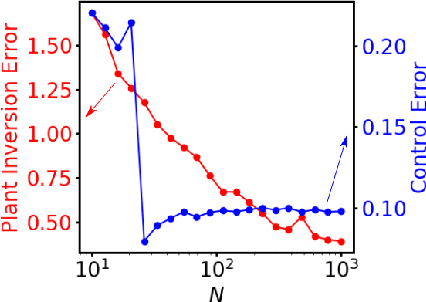
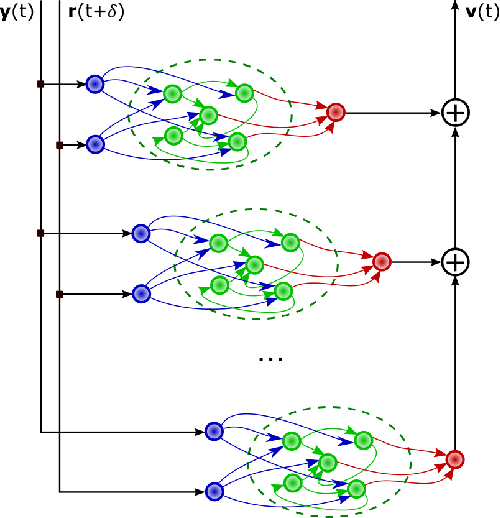
We propose and demonstrate a nonlinear control method that can be applied to unknown, complex systems where the controller is based on a type of artificial neural network known as a reservoir computer. In contrast to many modern neural-network-based control techniques, which are robust to system uncertainties but require a model nonetheless, our technique requires no prior knowledge of the system and is thus model-free. Further, our approach does not require an initial system identification step, resulting in a relatively simple and efficient learning process. Reservoir computers are well-suited to the control problem because they require small training data sets and remarkably low training times. By iteratively training and adding layers of reservoir computers to the controller, a precise and efficient control law is identified quickly. With examples on both numerical and high-speed experimental systems, we demonstrate that our approach is capable of controlling highly complex dynamical systems that display deterministic chaos to nontrivial target trajectories.

Combining Machine Learning with Knowledge-Based Modeling for Scalable Forecasting and Subgrid-Scale Closure of Large, Complex, Spatiotemporal Systems

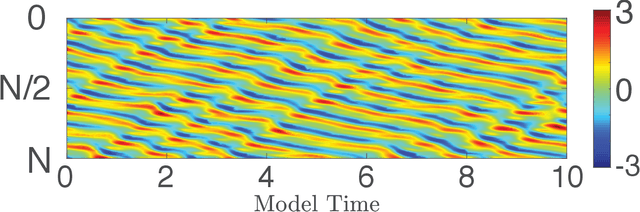
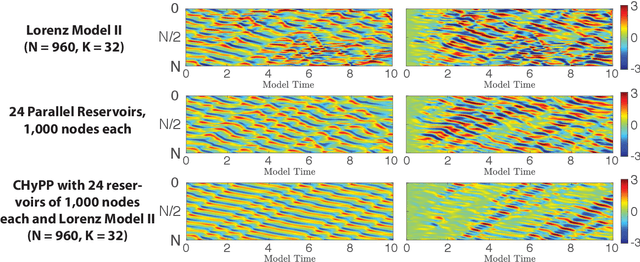
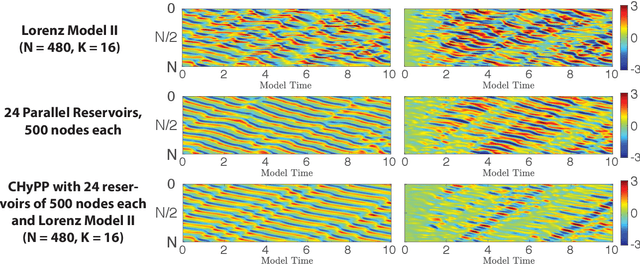
We consider the commonly encountered situation (e.g., in weather forecasting) where the goal is to predict the time evolution of a large, spatiotemporally chaotic dynamical system when we have access to both time series data of previous system states and an imperfect model of the full system dynamics. Specifically, we attempt to utilize machine learning as the essential tool for integrating the use of past data into predictions. In order to facilitate scalability to the common scenario of interest where the spatiotemporally chaotic system is very large and complex, we propose combining two approaches:(i) a parallel machine learning prediction scheme; and (ii) a hybrid technique, for a composite prediction system composed of a knowledge-based component and a machine-learning-based component. We demonstrate that not only can this method combining (i) and (ii) be scaled to give excellent performance for very large systems, but also that the length of time series data needed to train our multiple, parallel machine learning components is dramatically less than that necessary without parallelization. Furthermore, considering cases where computational realization of the knowledge-based component does not resolve subgrid-scale processes, our scheme is able to use training data to incorporate the effect of the unresolved short-scale dynamics upon the resolved longer-scale dynamics ("subgrid-scale closure").

Forecasting Chaotic Systems with Very Low Connectivity Reservoir Computers

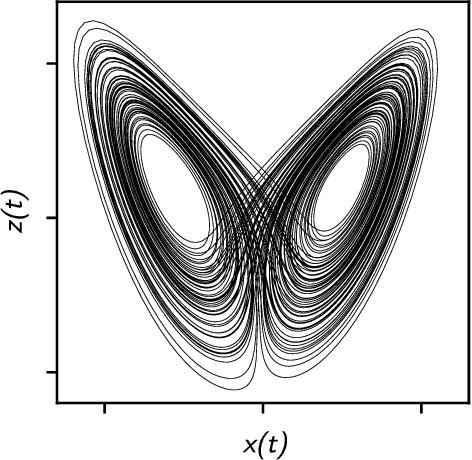
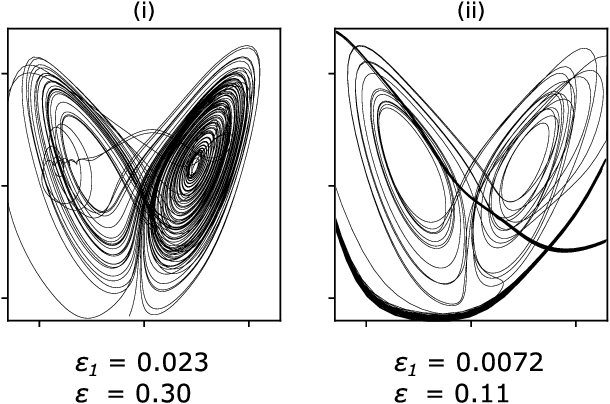
We explore the hyperparameter space of reservoir computers used for forecasting of the chaotic Lorenz '63 attractor with Bayesian optimization. We use a new measure of reservoir performance, designed to emphasize learning the global climate of the forecasted system rather than short-term prediction. We find that optimizing over this measure more quickly excludes reservoirs that fail to reproduce the climate. The results of optimization are surprising: the optimized parameters often specify a reservoir network with very low connectivity. Inspired by this observation, we explore reservoir designs with even simpler structure, and find well-performing reservoirs that have zero spectral radius and no recurrence. These simple reservoirs provide counterexamples to widely used heuristics in the field, and may be useful for hardware implementations of reservoir computers.