Exploring the Potential of Hybrid Machine-Learning/Physics-Based Modeling for Atmospheric/Oceanic Prediction Beyond the Medium Range

This paper explores the potential of a hybrid modeling approach that combines machine learning (ML) with conventional physics-based modeling for weather prediction beyond the medium range. It extends the work of Arcomano et al. (2022), which tested the approach for short- and medium-range weather prediction, and the work of Arcomano et al. (2023), which investigated its potential for climate modeling. The hybrid model used for the forecast experiments of the paper is based on the low-resolution, simplified parameterization atmospheric general circulation model (AGCM) SPEEDY. In addition to the hybridized prognostic variables of SPEEDY, the current version of the model has three purely ML-based prognostic variables. One of these is 6~h cumulative precipitation, another is the sea surface temperature, while the third is the heat content of the top 300 m deep layer of the ocean. The model has skill in predicting the El Ni\~no cycle and its global teleconnections with precipitation for 3-7 months depending on the season. The model captures equatorial variability of the precipitation associated with Kelvin and Rossby waves and MJO. Predictions of the precipitation in the equatorial region have skill for 15 days in the East Pacific and 11.5 days in the West Pacific. Though the model has low spatial resolution, for these tasks it has prediction skill comparable to what has been published for high-resolution, purely physics-based, conventional operational forecast models.

Combining Machine Learning with Knowledge-Based Modeling for Scalable Forecasting and Subgrid-Scale Closure of Large, Complex, Spatiotemporal Systems

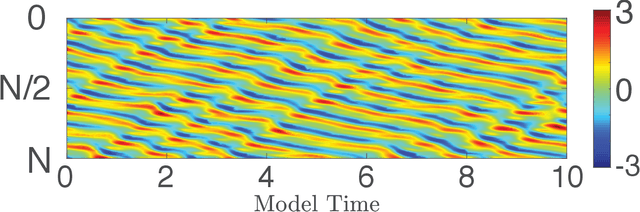
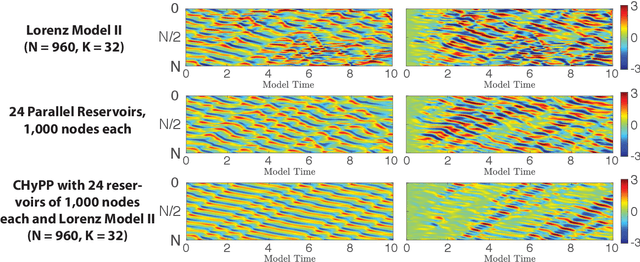
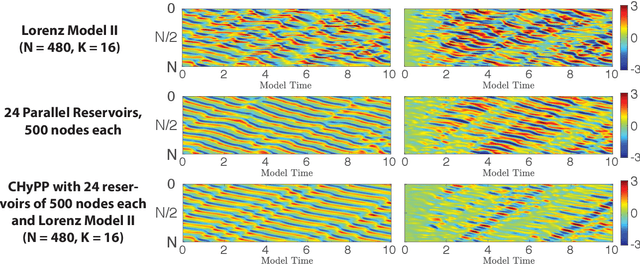
We consider the commonly encountered situation (e.g., in weather forecasting) where the goal is to predict the time evolution of a large, spatiotemporally chaotic dynamical system when we have access to both time series data of previous system states and an imperfect model of the full system dynamics. Specifically, we attempt to utilize machine learning as the essential tool for integrating the use of past data into predictions. In order to facilitate scalability to the common scenario of interest where the spatiotemporally chaotic system is very large and complex, we propose combining two approaches:(i) a parallel machine learning prediction scheme; and (ii) a hybrid technique, for a composite prediction system composed of a knowledge-based component and a machine-learning-based component. We demonstrate that not only can this method combining (i) and (ii) be scaled to give excellent performance for very large systems, but also that the length of time series data needed to train our multiple, parallel machine learning components is dramatically less than that necessary without parallelization. Furthermore, considering cases where computational realization of the knowledge-based component does not resolve subgrid-scale processes, our scheme is able to use training data to incorporate the effect of the unresolved short-scale dynamics upon the resolved longer-scale dynamics ("subgrid-scale closure").

Separation of Chaotic Signals by Reservoir Computing

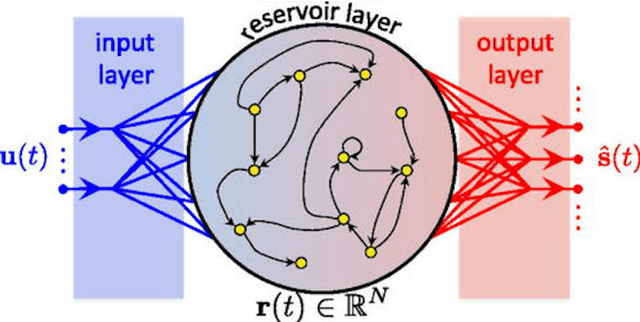
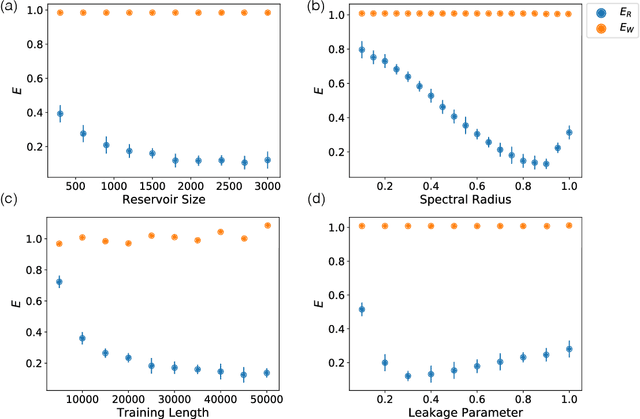
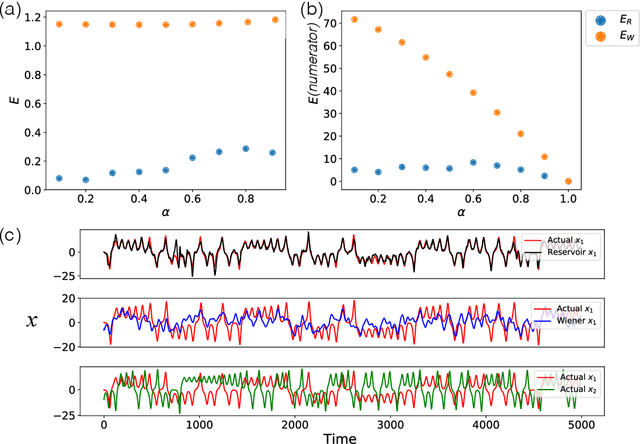
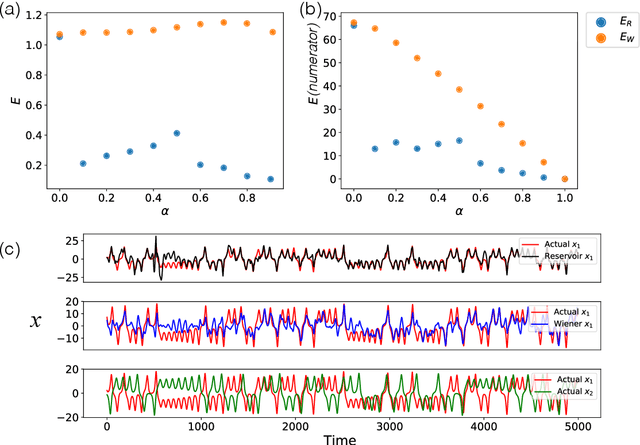
We demonstrate the utility of machine learning in the separation of superimposed chaotic signals using a technique called Reservoir Computing. We assume no knowledge of the dynamical equations that produce the signals, and require only training data consisting of finite time samples of the component signals. We test our method on signals that are formed as linear combinations of signals from two Lorenz systems with different parameters. Comparing our nonlinear method with the optimal linear solution to the separation problem, the Wiener filter, we find that our method significantly outperforms the Wiener filter in all the scenarios we study. Furthermore, this difference is particularly striking when the component signals have similar frequency spectra. Indeed, our method works well when the component frequency spectra are indistinguishable - a case where a Wiener filter performs essentially no separation.

Hybrid Forecasting of Chaotic Processes: Using Machine Learning in Conjunction with a Knowledge-Based Model

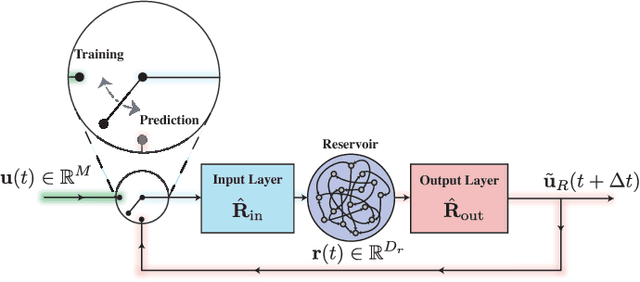
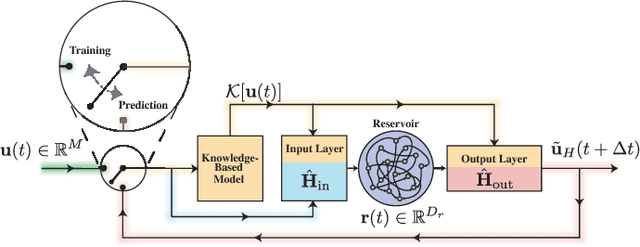
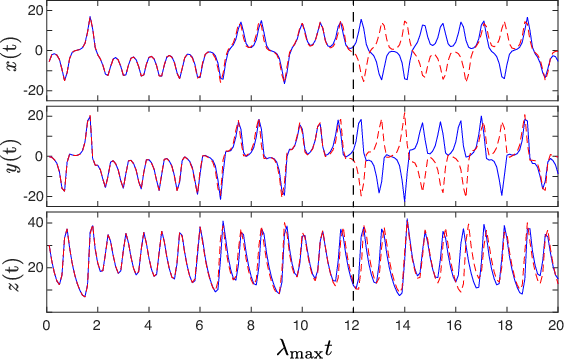
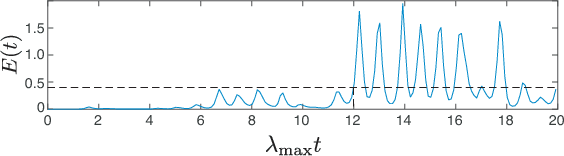
A model-based approach to forecasting chaotic dynamical systems utilizes knowledge of the physical processes governing the dynamics to build an approximate mathematical model of the system. In contrast, machine learning techniques have demonstrated promising results for forecasting chaotic systems purely from past time series measurements of system state variables (training data), without prior knowledge of the system dynamics. The motivation for this paper is the potential of machine learning for filling in the gaps in our underlying mechanistic knowledge that cause widely-used knowledge-based models to be inaccurate. Thus we here propose a general method that leverages the advantages of these two approaches by combining a knowledge-based model and a machine learning technique to build a hybrid forecasting scheme. Potential applications for such an approach are numerous (e.g., improving weather forecasting). We demonstrate and test the utility of this approach using a particular illustrative version of a machine learning known as reservoir computing, and we apply the resulting hybrid forecaster to a low-dimensional chaotic system, as well as to a high-dimensional spatiotemporal chaotic system. These tests yield extremely promising results in that our hybrid technique is able to accurately predict for a much longer period of time than either its machine-learning component or its model-based component alone.