Separation of Chaotic Signals by Reservoir Computing
Paper and Code
Oct 25, 2019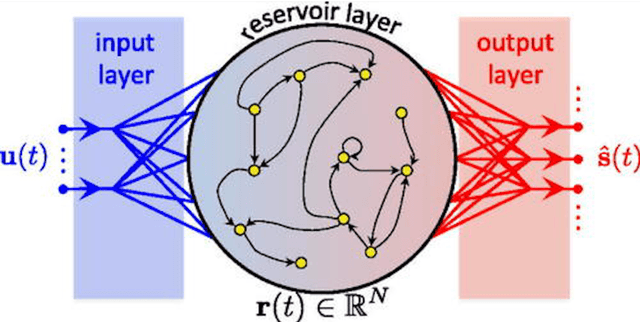
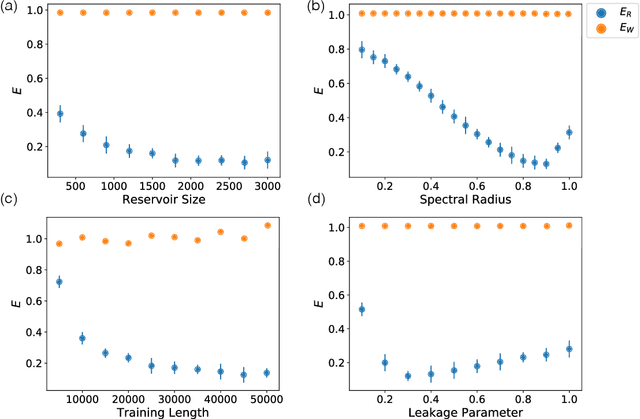
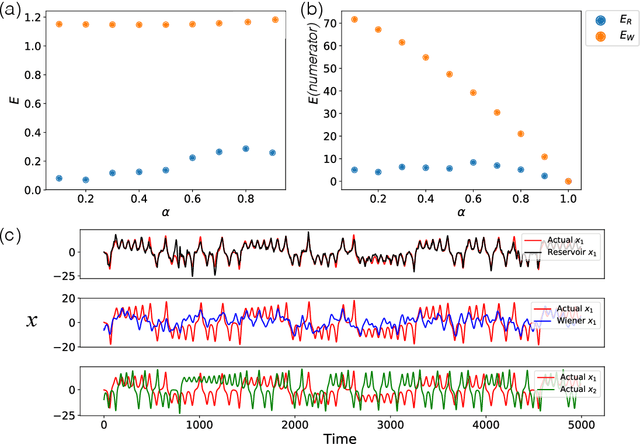
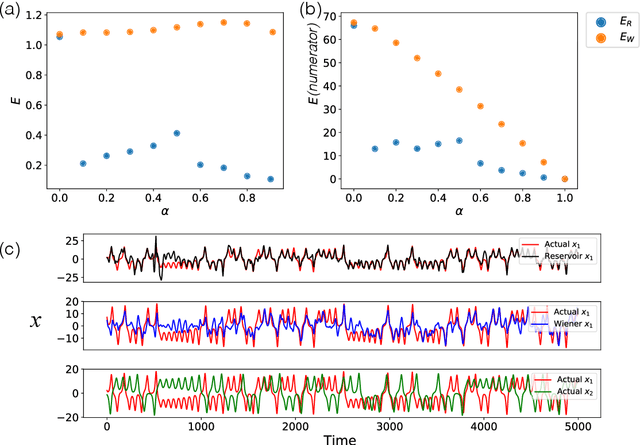
We demonstrate the utility of machine learning in the separation of superimposed chaotic signals using a technique called Reservoir Computing. We assume no knowledge of the dynamical equations that produce the signals, and require only training data consisting of finite time samples of the component signals. We test our method on signals that are formed as linear combinations of signals from two Lorenz systems with different parameters. Comparing our nonlinear method with the optimal linear solution to the separation problem, the Wiener filter, we find that our method significantly outperforms the Wiener filter in all the scenarios we study. Furthermore, this difference is particularly striking when the component signals have similar frequency spectra. Indeed, our method works well when the component frequency spectra are indistinguishable - a case where a Wiener filter performs essentially no separation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge