Graph Neural Tangent Kernel: Convergence on Large Graphs

Graph neural networks (GNNs) achieve remarkable performance in graph machine learning tasks but can be hard to train on large-graph data, where their learning dynamics are not well understood. We investigate the training dynamics of large-graph GNNs using graph neural tangent kernels (GNTKs) and graphons. In the limit of large width, optimization of an overparametrized NN is equivalent to kernel regression on the NTK. Here, we investigate how the GNTK evolves as another independent dimension is varied: the graph size. We use graphons to define limit objects -- graphon NNs for GNNs, and graphon NTKs for GNTKs, and prove that, on a sequence of growing graphs, the GNTKs converge to the graphon NTK. We further prove that the eigenspaces of the GNTK, which are related to the problem learning directions and associated learning speeds, converge to the spectrum of the GNTK. This implies that in the large-graph limit, the GNTK fitted on a graph of moderate size can be used to solve the same task on the large-graph and infer the learning dynamics of the large-graph GNN. These results are verified empirically on node regression and node classification tasks.

Encoding priors in the brain: a reinforcement learning model for mouse decision making

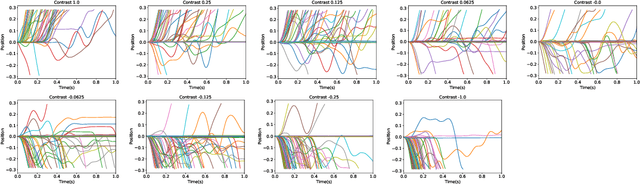
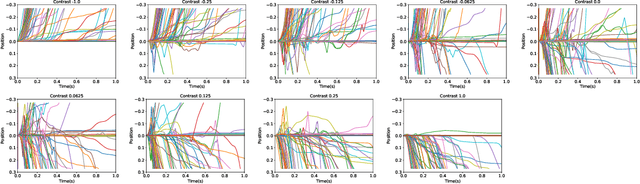
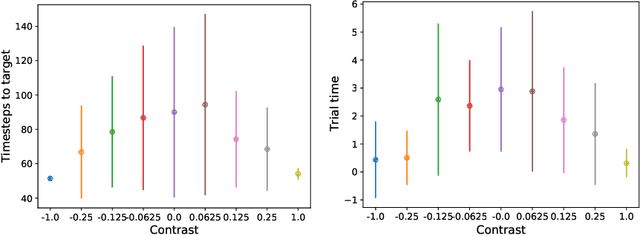
In two-alternative forced choice tasks, prior knowledge can improve performance, especially when operating near the psychophysical threshold. For instance, if subjects know that one choice is much more likely than the other, they can make that choice when evidence is weak. A common hypothesis for these kinds of tasks is that the prior is stored in neural activity. Here we propose a different hypothesis: the prior is stored in synaptic strengths. We study the International Brain Laboratory task, in which a grating appears on either the right or left side of a screen, and a mouse has to move a wheel to bring the grating to the center. The grating is often low in contrast which makes the task relatively difficult, and the prior probability that the grating appears on the right is either 80% or 20%, in (unsignaled) blocks of about 50 trials. We model this as a reinforcement learning task, using a feedforward neural network to map states to actions, and adjust the weights of the network to maximize reward, learning via policy gradient. Our model uses an internal state that stores an estimate of the grating and confidence, and follows Bayesian updates, and can switch between engaged and disengaged states to mimic animal behavior. This model reproduces the main experimental finding - that the psychometric curve with respect to contrast shifts after a block switch in about 10 trials. Also, as seen in the experiments, in our model the difference in neuronal activity in the right and left blocks is small - it is virtually impossible to decode block structure from activity on single trials if noise is about 2%. The hypothesis that priors are stored in weights is difficult to test, but the technology to do so should be available in the not so distant future.

Stroke recovery phenotyping through network trajectory approaches and graph neural networks

Stroke is a leading cause of neurological injury characterized by impairments in multiple neurological domains including cognition, language, sensory and motor functions. Clinical recovery in these domains is tracked using a wide range of measures that may be continuous, ordinal, interval or categorical in nature, which presents challenges for standard multivariate regression approaches. This has hindered stroke researchers' ability to achieve an integrated picture of the complex time-evolving interactions amongst symptoms. Here we use tools from network science and machine learning that are particularly well-suited to extracting underlying patterns in such data, and may assist in prediction of recovery patterns. To demonstrate the utility of this approach, we analyzed data from the NINDS tPA trial using the Trajectory Profile Clustering (TPC) method to identify distinct stroke recovery patterns for 11 different neurological domains at 5 discrete time points. Our analysis identified 3 distinct stroke trajectory profiles that align with clinically relevant stroke syndromes, characterized both by distinct clusters of symptoms, as well as differing degrees of symptom severity. We then validated our approach using graph neural networks to determine how well our model performed predictively for stratifying patients into these trajectory profiles at early vs. later time points post-stroke. We demonstrate that trajectory profile clustering is an effective method for identifying clinically relevant recovery subtypes in multidimensional longitudinal datasets, and for early prediction of symptom progression subtypes in individual patients. This paper is the first work introducing network trajectory approaches for stroke recovery phenotyping, and is aimed at enhancing the translation of such novel computational approaches for practical clinical application.

Encoded Prior Sliced Wasserstein AutoEncoder for learning latent manifold representations

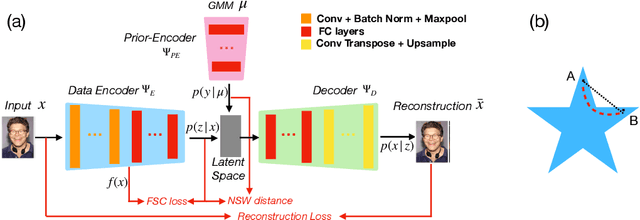
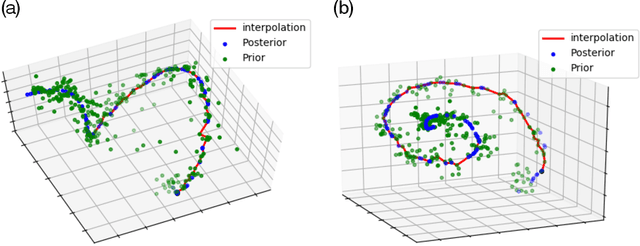
While variational autoencoders have been successful generative models for a variety of tasks, the use of conventional Gaussian or Gaussian mixture priors are limited in their ability to capture topological or geometric properties of data in the latent representation. In this work, we introduce an Encoded Prior Sliced Wasserstein AutoEncoder (EPSWAE) wherein an additional prior-encoder network learns an unconstrained prior to match the encoded data manifold. The autoencoder and prior-encoder networks are iteratively trained using the Sliced Wasserstein Distance (SWD), which efficiently measures the distance between two $\textit{arbitrary}$ sampleable distributions without being constrained to a specific form as in the KL divergence, and without requiring expensive adversarial training. Additionally, we enhance the conventional SWD by introducing a nonlinear shearing, i.e., averaging over random $\textit{nonlinear}$ transformations, to better capture differences between two distributions. The prior is further encouraged to encode the data manifold by use of a structural consistency term that encourages isometry between feature space and latent space. Lastly, interpolation along $\textit{geodesics}$ on the latent space representation of the data manifold generates samples that lie on the manifold and hence is advantageous compared with standard Euclidean interpolation. To this end, we introduce a graph-based algorithm for identifying network-geodesics in latent space from samples of the prior that maximize the density of samples along the path while minimizing total energy. We apply our framework to 3D-spiral, MNIST, and CelebA datasets, and show that its latent representations and interpolations are comparable to the state of the art on equivalent architectures.

Separation of Chaotic Signals by Reservoir Computing

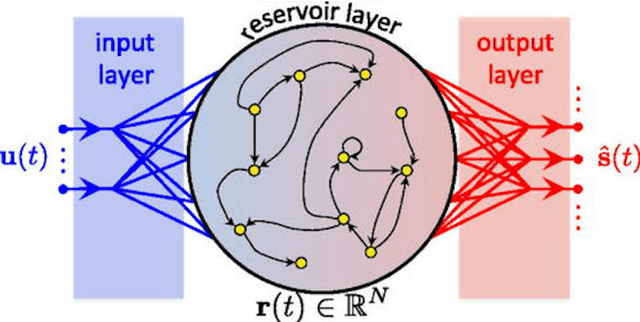
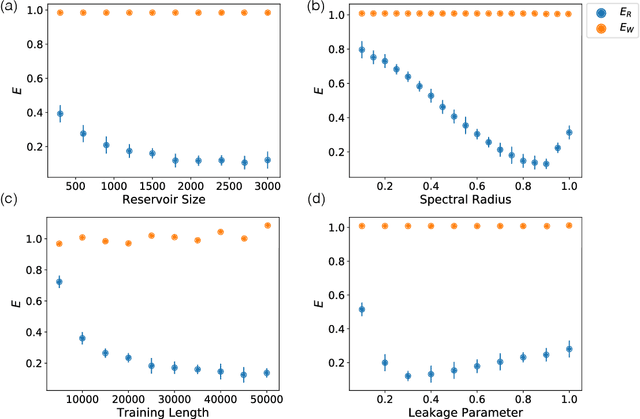
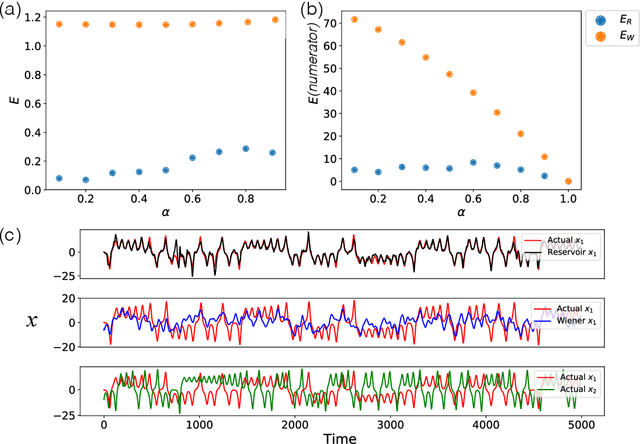
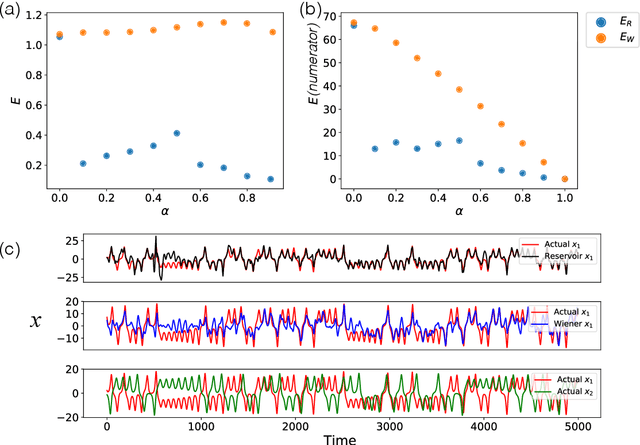
We demonstrate the utility of machine learning in the separation of superimposed chaotic signals using a technique called Reservoir Computing. We assume no knowledge of the dynamical equations that produce the signals, and require only training data consisting of finite time samples of the component signals. We test our method on signals that are formed as linear combinations of signals from two Lorenz systems with different parameters. Comparing our nonlinear method with the optimal linear solution to the separation problem, the Wiener filter, we find that our method significantly outperforms the Wiener filter in all the scenarios we study. Furthermore, this difference is particularly striking when the component signals have similar frequency spectra. Indeed, our method works well when the component frequency spectra are indistinguishable - a case where a Wiener filter performs essentially no separation.