Graph Neural Tangent Kernel: Convergence on Large Graphs
Paper and Code
Jan 25, 2023
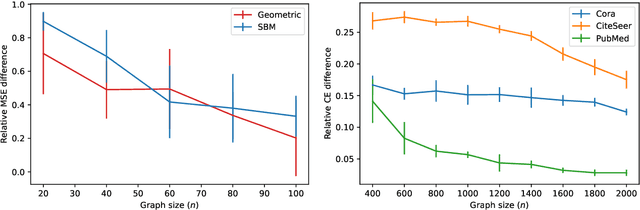
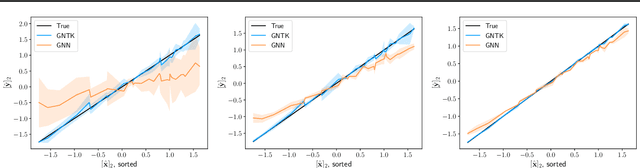
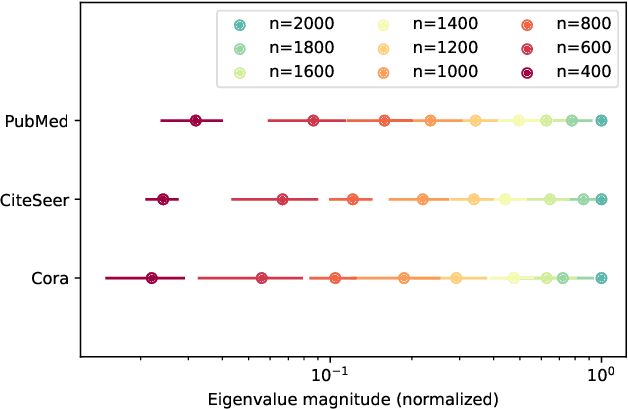
Graph neural networks (GNNs) achieve remarkable performance in graph machine learning tasks but can be hard to train on large-graph data, where their learning dynamics are not well understood. We investigate the training dynamics of large-graph GNNs using graph neural tangent kernels (GNTKs) and graphons. In the limit of large width, optimization of an overparametrized NN is equivalent to kernel regression on the NTK. Here, we investigate how the GNTK evolves as another independent dimension is varied: the graph size. We use graphons to define limit objects -- graphon NNs for GNNs, and graphon NTKs for GNTKs, and prove that, on a sequence of growing graphs, the GNTKs converge to the graphon NTK. We further prove that the eigenspaces of the GNTK, which are related to the problem learning directions and associated learning speeds, converge to the spectrum of the GNTK. This implies that in the large-graph limit, the GNTK fitted on a graph of moderate size can be used to solve the same task on the large-graph and infer the learning dynamics of the large-graph GNN. These results are verified empirically on node regression and node classification tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge