Stabilizing Machine Learning Prediction of Dynamics: Noise and Noise-inspired Regularization

Recent work has shown that machine learning (ML) models can be trained to accurately forecast the dynamics of unknown chaotic dynamical systems. Such ML models can be used to produce both short-term predictions of the state evolution and long-term predictions of the statistical patterns of the dynamics (``climate''). Both of these tasks can be accomplished by employing a feedback loop, whereby the model is trained to predict forward one time step, then the trained model is iterated for multiple time steps with its output used as the input. In the absence of mitigating techniques, however, this technique can result in artificially rapid error growth, leading to inaccurate predictions and/or climate instability. In this article, we systematically examine the technique of adding noise to the ML model input during training as a means to promote stability and improve prediction accuracy. Furthermore, we introduce Linearized Multi-Noise Training (LMNT), a regularization technique that deterministically approximates the effect of many small, independent noise realizations added to the model input during training. Our case study uses reservoir computing, a machine-learning method using recurrent neural networks, to predict the spatiotemporal chaotic Kuramoto-Sivashinsky equation. We find that reservoir computers trained with noise or with LMNT produce climate predictions that appear to be indefinitely stable and have a climate very similar to the true system, while reservoir computers trained without regularization are unstable. Compared with other types of regularization that yield stability in some cases, we find that both short-term and climate predictions from reservoir computers trained with noise or with LMNT are substantially more accurate. Finally, we show that the deterministic aspect of our LMNT regularization facilitates fast hyperparameter tuning when compared to training with noise.

A Meta-learning Approach to Reservoir Computing: Time Series Prediction with Limited Data

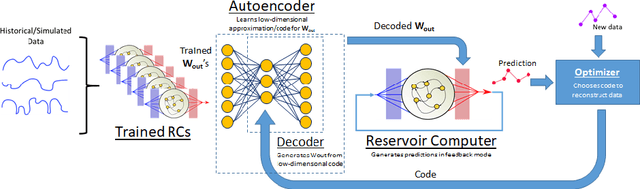
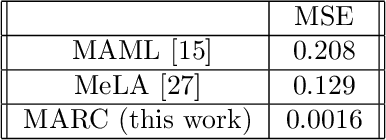
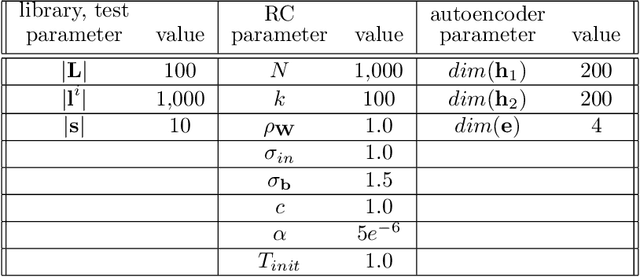
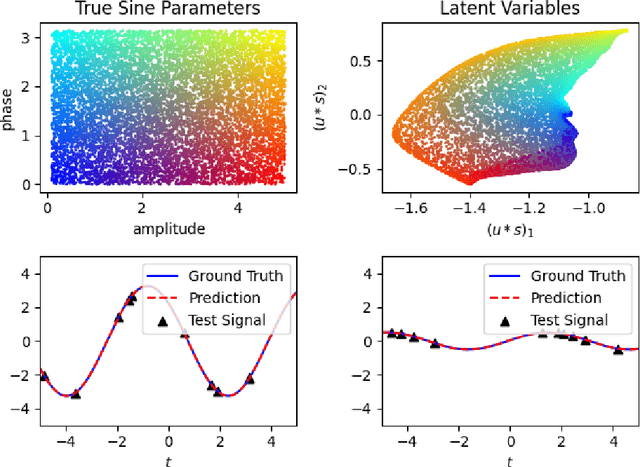
Recent research has established the effectiveness of machine learning for data-driven prediction of the future evolution of unknown dynamical systems, including chaotic systems. However, these approaches require large amounts of measured time series data from the process to be predicted. When only limited data is available, forecasters are forced to impose significant model structure that may or may not accurately represent the process of interest. In this work, we present a Meta-learning Approach to Reservoir Computing (MARC), a data-driven approach to automatically extract an appropriate model structure from experimentally observed "related" processes that can be used to vastly reduce the amount of data required to successfully train a predictive model. We demonstrate our approach on a simple benchmark problem, where it beats the state of the art meta-learning techniques, as well as a challenging chaotic problem.

Parallel Machine Learning for Forecasting the Dynamics of Complex Networks

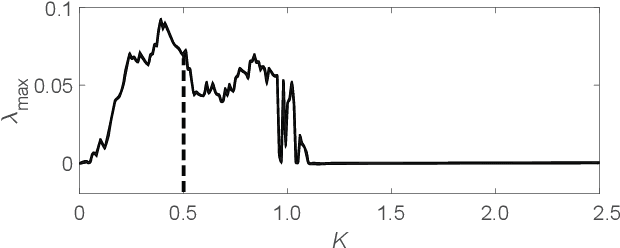
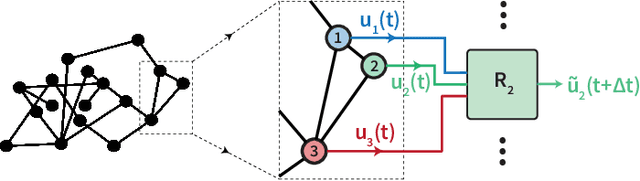
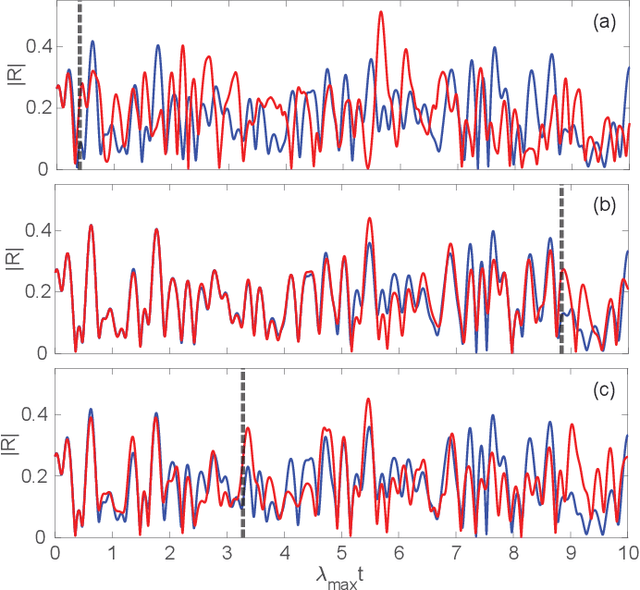
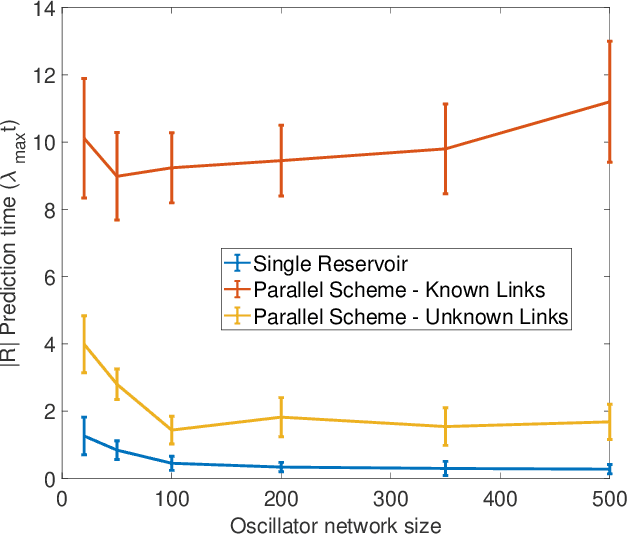
Forecasting the dynamics of large complex networks from previous time-series data is important in a wide range of contexts. Here we present a machine learning scheme for this task using a parallel architecture that mimics the topology of the network of interest. We demonstrate the utility and scalability of our method implemented using reservoir computing on a chaotic network of oscillators. Two levels of prior knowledge are considered: (i) the network links are known; and (ii) the network links are unknown and inferred via a data-driven approach to approximately optimize prediction.

Using Data Assimilation to Train a Hybrid Forecast System that Combines Machine-Learning and Knowledge-Based Components

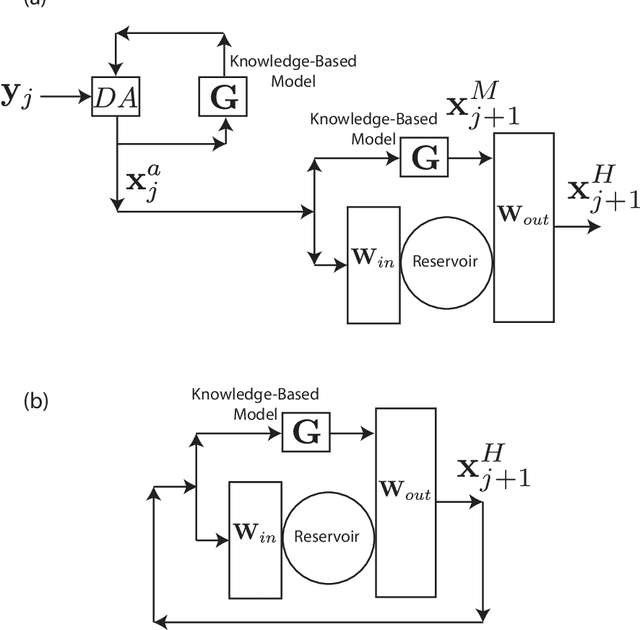
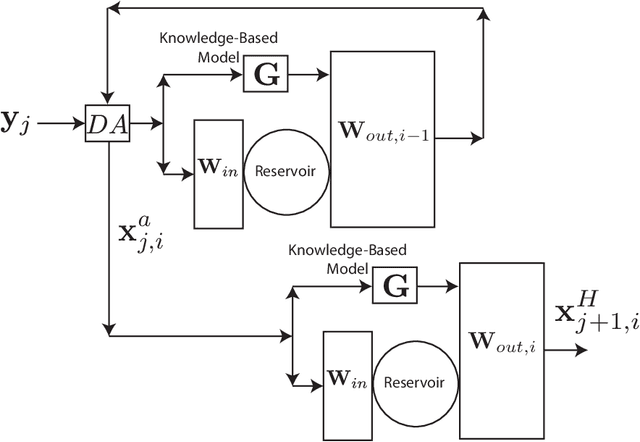
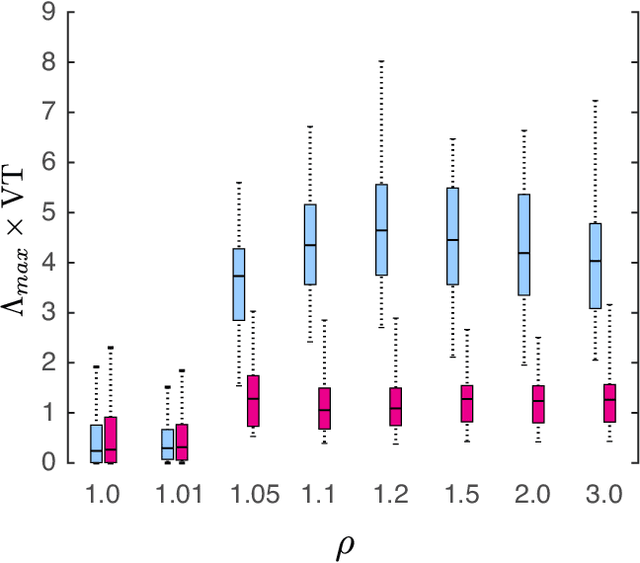
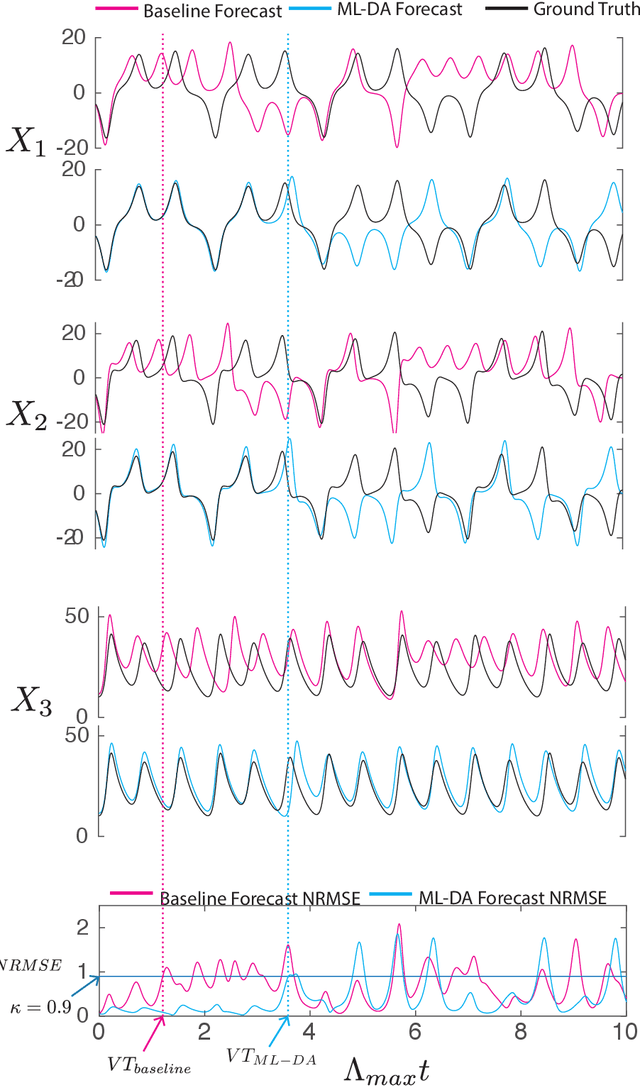
We consider the problem of data-assisted forecasting of chaotic dynamical systems when the available data is in the form of noisy partial measurements of the past and present state of the dynamical system. Recently there have been several promising data-driven approaches to forecasting of chaotic dynamical systems using machine learning. Particularly promising among these are hybrid approaches that combine machine learning with a knowledge-based model, where a machine-learning technique is used to correct the imperfections in the knowledge-based model. Such imperfections may be due to incomplete understanding and/or limited resolution of the physical processes in the underlying dynamical system, e.g., the atmosphere or the ocean. Previously proposed data-driven forecasting approaches tend to require, for training, measurements of all the variables that are intended to be forecast. We describe a way to relax this assumption by combining data assimilation with machine learning. We demonstrate this technique using the Ensemble Transform Kalman Filter (ETKF) to assimilate synthetic data for the 3-variable Lorenz system and for the Kuramoto-Sivashinsky system, simulating model error in each case by a misspecified parameter value. We show that by using partial measurements of the state of the dynamical system, we can train a machine learning model to improve predictions made by an imperfect knowledge-based model.

Hybrid Backpropagation Parallel Reservoir Networks

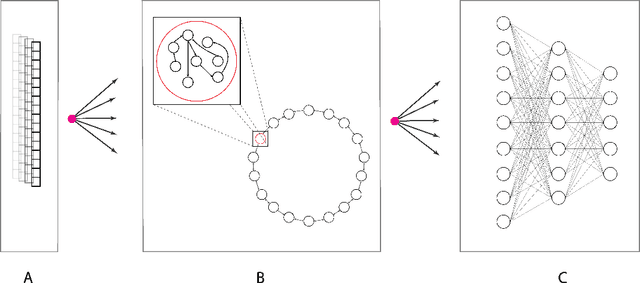
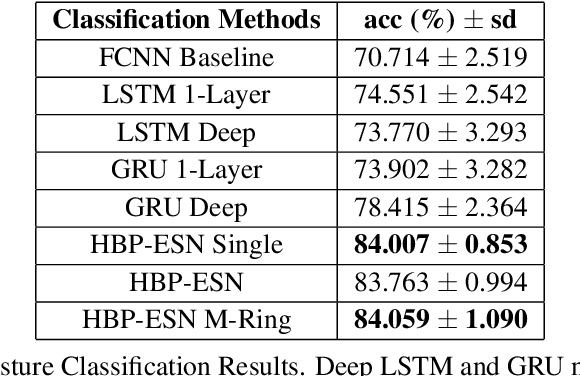
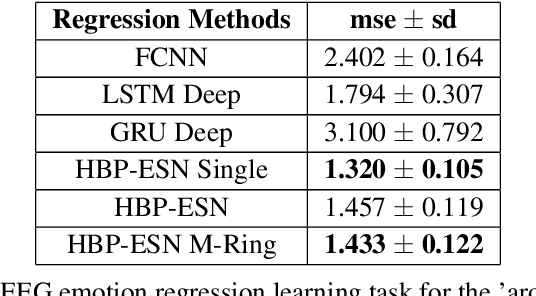
In many real-world applications, fully-differentiable RNNs such as LSTMs and GRUs have been widely deployed to solve time series learning tasks. These networks train via Backpropagation Through Time, which can work well in practice but involves a biologically unrealistic unrolling of the network in time for gradient updates, are computationally expensive, and can be hard to tune. A second paradigm, Reservoir Computing, keeps the recurrent weight matrix fixed and random. Here, we propose a novel hybrid network, which we call Hybrid Backpropagation Parallel Echo State Network (HBP-ESN) which combines the effectiveness of learning random temporal features of reservoirs with the readout power of a deep neural network with batch normalization. We demonstrate that our new network outperforms LSTMs and GRUs, including multi-layer "deep" versions of these networks, on two complex real-world multi-dimensional time series datasets: gesture recognition using skeleton keypoints from ChaLearn, and the DEAP dataset for emotion recognition from EEG measurements. We show also that the inclusion of a novel meta-ring structure, which we call HBP-ESN M-Ring, achieves similar performance to one large reservoir while decreasing the memory required by an order of magnitude. We thus offer this new hybrid reservoir deep learning paradigm as a new alternative direction for RNN learning of temporal or sequential data.

Combining Machine Learning with Knowledge-Based Modeling for Scalable Forecasting and Subgrid-Scale Closure of Large, Complex, Spatiotemporal Systems

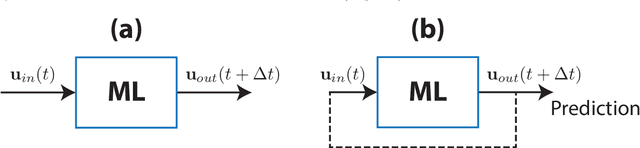
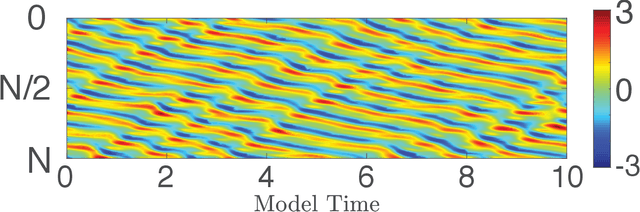
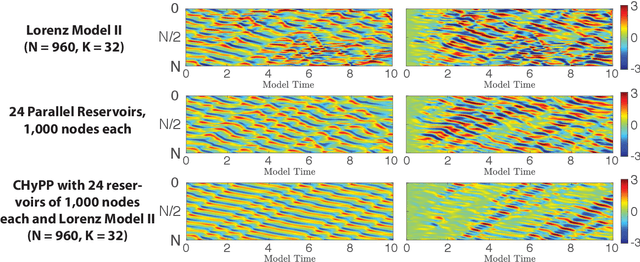
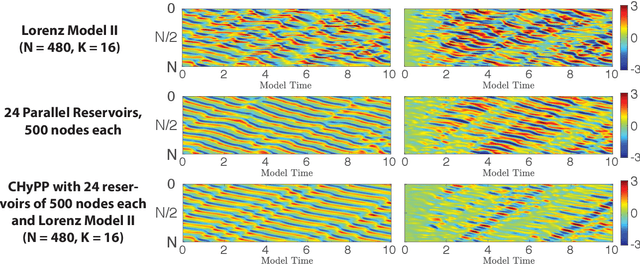
We consider the commonly encountered situation (e.g., in weather forecasting) where the goal is to predict the time evolution of a large, spatiotemporally chaotic dynamical system when we have access to both time series data of previous system states and an imperfect model of the full system dynamics. Specifically, we attempt to utilize machine learning as the essential tool for integrating the use of past data into predictions. In order to facilitate scalability to the common scenario of interest where the spatiotemporally chaotic system is very large and complex, we propose combining two approaches:(i) a parallel machine learning prediction scheme; and (ii) a hybrid technique, for a composite prediction system composed of a knowledge-based component and a machine-learning-based component. We demonstrate that not only can this method combining (i) and (ii) be scaled to give excellent performance for very large systems, but also that the length of time series data needed to train our multiple, parallel machine learning components is dramatically less than that necessary without parallelization. Furthermore, considering cases where computational realization of the knowledge-based component does not resolve subgrid-scale processes, our scheme is able to use training data to incorporate the effect of the unresolved short-scale dynamics upon the resolved longer-scale dynamics ("subgrid-scale closure").

Separation of Chaotic Signals by Reservoir Computing

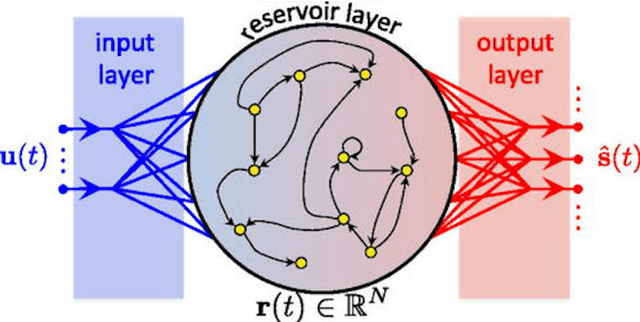
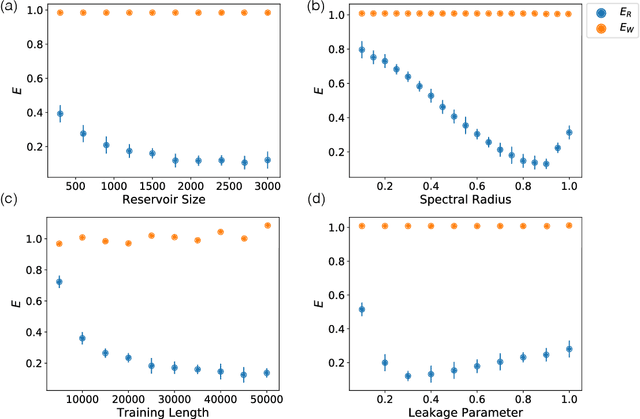
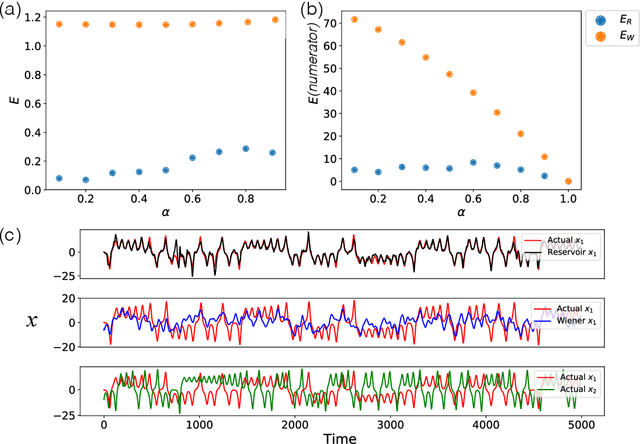
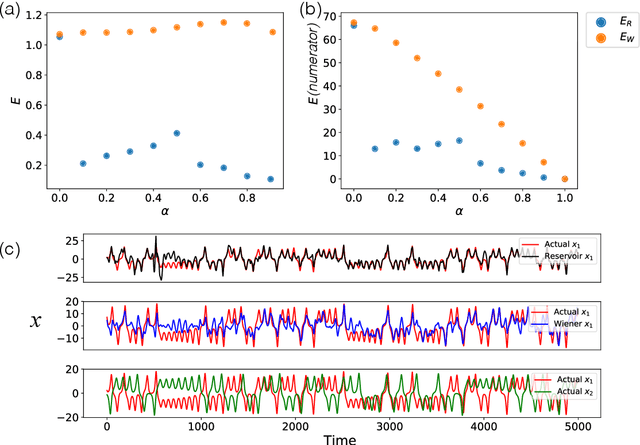
We demonstrate the utility of machine learning in the separation of superimposed chaotic signals using a technique called Reservoir Computing. We assume no knowledge of the dynamical equations that produce the signals, and require only training data consisting of finite time samples of the component signals. We test our method on signals that are formed as linear combinations of signals from two Lorenz systems with different parameters. Comparing our nonlinear method with the optimal linear solution to the separation problem, the Wiener filter, we find that our method significantly outperforms the Wiener filter in all the scenarios we study. Furthermore, this difference is particularly striking when the component signals have similar frequency spectra. Indeed, our method works well when the component frequency spectra are indistinguishable - a case where a Wiener filter performs essentially no separation.

Forecasting of Spatio-temporal Chaotic Dynamics with Recurrent Neural Networks: a comparative study of Reservoir Computing and Backpropagation Algorithms

How effective are Recurrent Neural Networks (RNNs) in forecasting the spatiotemporal dynamics of chaotic systems ? We address this question through a comparative study of Reservoir Computing (RC) and backpropagation through time (BPTT) algorithms for gated network architectures on a number of benchmark problems. We quantify their relative prediction accuracy on the long-term forecasting of Lorenz-96 and the Kuramoto-Sivashinsky equation and calculation of its Lyapunov spectrum. We discuss their implementation on parallel computers and highlight advantages and limitations of each method. We find that, when the full state dynamics are available for training, RC outperforms BPTT approaches in terms of predictive performance and capturing of the long-term statistics, while at the same time requiring much less time for training. However, in the case of reduced order data, large RC models can be unstable and more likely, than the BPTT algorithms, to diverge in the long term. In contrast, RNNs trained via BPTT capture well the dynamics of these reduced order models. This study confirms that RNNs present a potent computational framework for the forecasting of complex spatio-temporal dynamics.

Hybrid Forecasting of Chaotic Processes: Using Machine Learning in Conjunction with a Knowledge-Based Model

A model-based approach to forecasting chaotic dynamical systems utilizes knowledge of the physical processes governing the dynamics to build an approximate mathematical model of the system. In contrast, machine learning techniques have demonstrated promising results for forecasting chaotic systems purely from past time series measurements of system state variables (training data), without prior knowledge of the system dynamics. The motivation for this paper is the potential of machine learning for filling in the gaps in our underlying mechanistic knowledge that cause widely-used knowledge-based models to be inaccurate. Thus we here propose a general method that leverages the advantages of these two approaches by combining a knowledge-based model and a machine learning technique to build a hybrid forecasting scheme. Potential applications for such an approach are numerous (e.g., improving weather forecasting). We demonstrate and test the utility of this approach using a particular illustrative version of a machine learning known as reservoir computing, and we apply the resulting hybrid forecaster to a low-dimensional chaotic system, as well as to a high-dimensional spatiotemporal chaotic system. These tests yield extremely promising results in that our hybrid technique is able to accurately predict for a much longer period of time than either its machine-learning component or its model-based component alone.