Exploring the Potential of Hybrid Machine-Learning/Physics-Based Modeling for Atmospheric/Oceanic Prediction Beyond the Medium Range

This paper explores the potential of a hybrid modeling approach that combines machine learning (ML) with conventional physics-based modeling for weather prediction beyond the medium range. It extends the work of Arcomano et al. (2022), which tested the approach for short- and medium-range weather prediction, and the work of Arcomano et al. (2023), which investigated its potential for climate modeling. The hybrid model used for the forecast experiments of the paper is based on the low-resolution, simplified parameterization atmospheric general circulation model (AGCM) SPEEDY. In addition to the hybridized prognostic variables of SPEEDY, the current version of the model has three purely ML-based prognostic variables. One of these is 6~h cumulative precipitation, another is the sea surface temperature, while the third is the heat content of the top 300 m deep layer of the ocean. The model has skill in predicting the El Ni\~no cycle and its global teleconnections with precipitation for 3-7 months depending on the season. The model captures equatorial variability of the precipitation associated with Kelvin and Rossby waves and MJO. Predictions of the precipitation in the equatorial region have skill for 15 days in the East Pacific and 11.5 days in the West Pacific. Though the model has low spatial resolution, for these tasks it has prediction skill comparable to what has been published for high-resolution, purely physics-based, conventional operational forecast models.

Using Data Assimilation to Train a Hybrid Forecast System that Combines Machine-Learning and Knowledge-Based Components

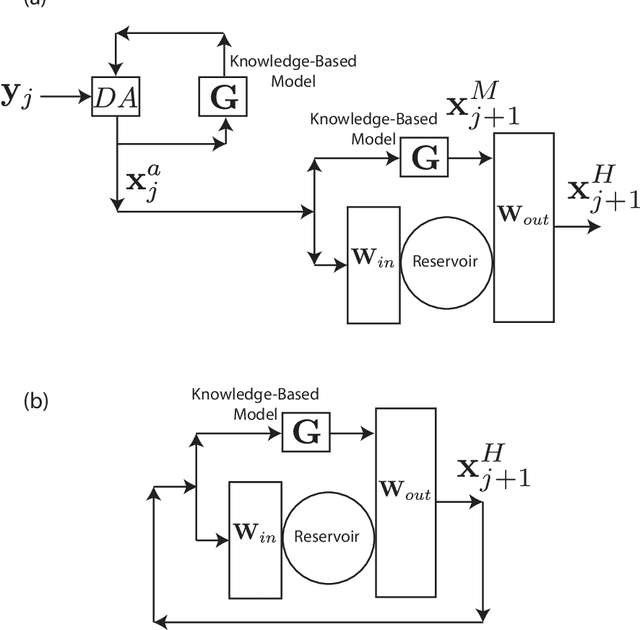
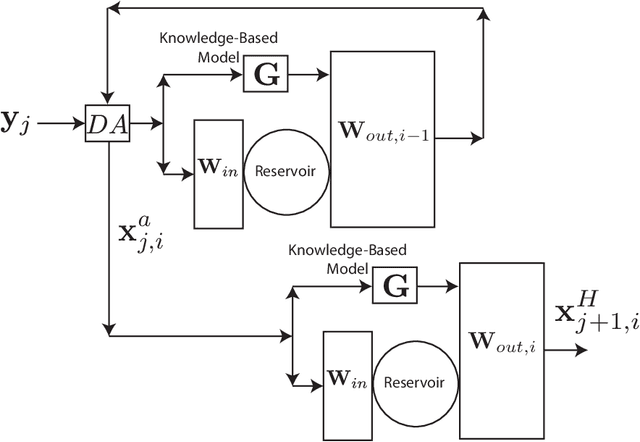
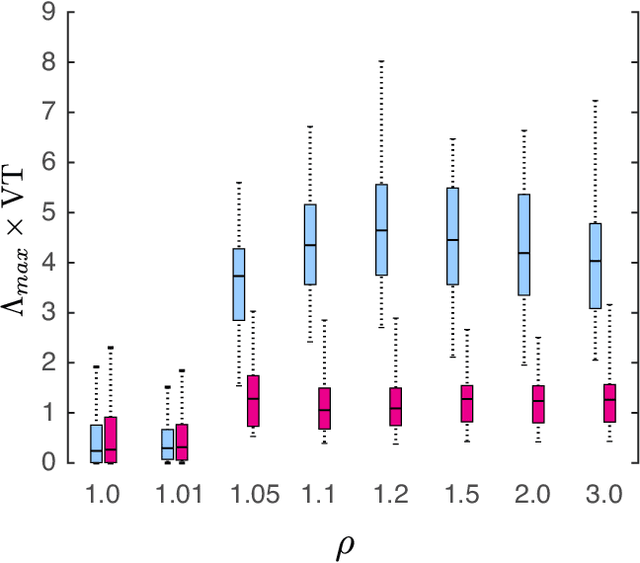
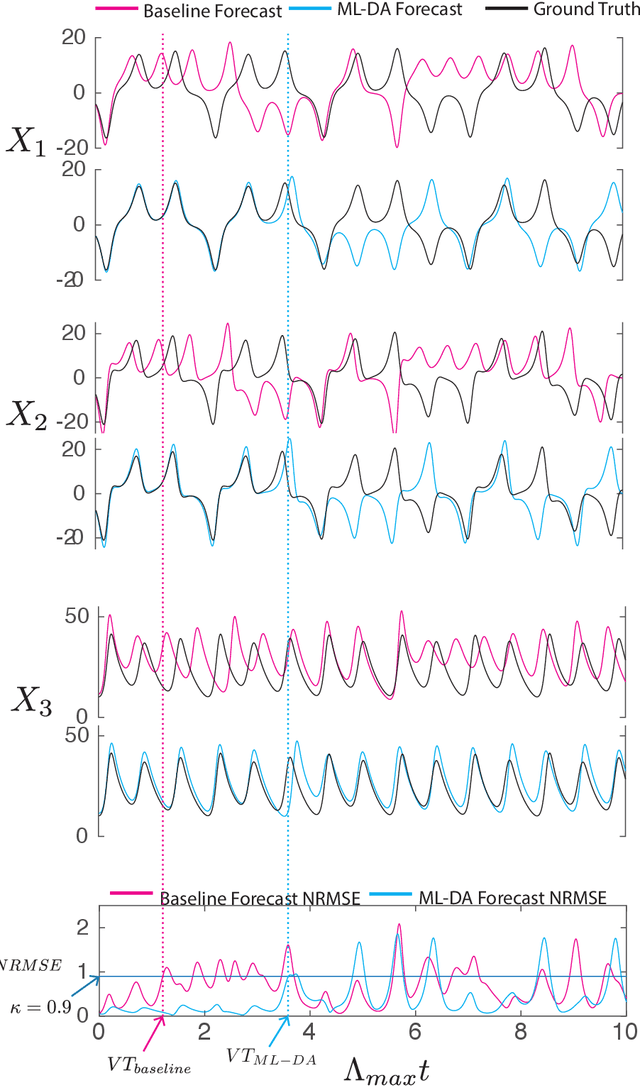
We consider the problem of data-assisted forecasting of chaotic dynamical systems when the available data is in the form of noisy partial measurements of the past and present state of the dynamical system. Recently there have been several promising data-driven approaches to forecasting of chaotic dynamical systems using machine learning. Particularly promising among these are hybrid approaches that combine machine learning with a knowledge-based model, where a machine-learning technique is used to correct the imperfections in the knowledge-based model. Such imperfections may be due to incomplete understanding and/or limited resolution of the physical processes in the underlying dynamical system, e.g., the atmosphere or the ocean. Previously proposed data-driven forecasting approaches tend to require, for training, measurements of all the variables that are intended to be forecast. We describe a way to relax this assumption by combining data assimilation with machine learning. We demonstrate this technique using the Ensemble Transform Kalman Filter (ETKF) to assimilate synthetic data for the 3-variable Lorenz system and for the Kuramoto-Sivashinsky system, simulating model error in each case by a misspecified parameter value. We show that by using partial measurements of the state of the dynamical system, we can train a machine learning model to improve predictions made by an imperfect knowledge-based model.

Combining Machine Learning with Knowledge-Based Modeling for Scalable Forecasting and Subgrid-Scale Closure of Large, Complex, Spatiotemporal Systems

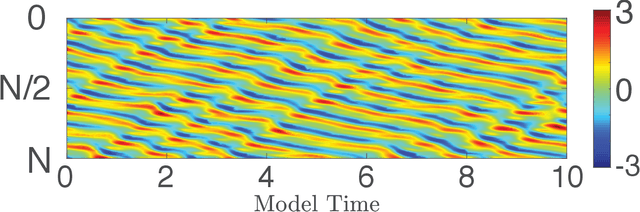
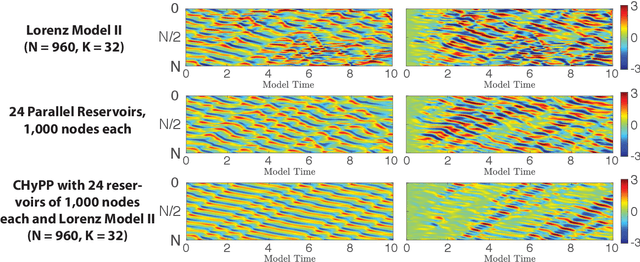
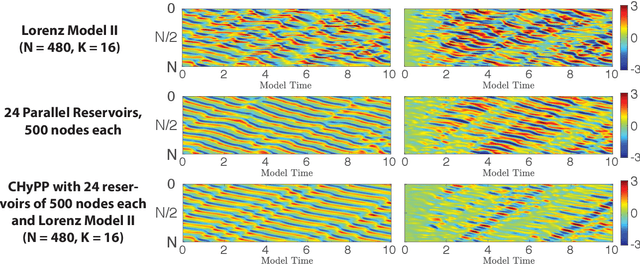
We consider the commonly encountered situation (e.g., in weather forecasting) where the goal is to predict the time evolution of a large, spatiotemporally chaotic dynamical system when we have access to both time series data of previous system states and an imperfect model of the full system dynamics. Specifically, we attempt to utilize machine learning as the essential tool for integrating the use of past data into predictions. In order to facilitate scalability to the common scenario of interest where the spatiotemporally chaotic system is very large and complex, we propose combining two approaches:(i) a parallel machine learning prediction scheme; and (ii) a hybrid technique, for a composite prediction system composed of a knowledge-based component and a machine-learning-based component. We demonstrate that not only can this method combining (i) and (ii) be scaled to give excellent performance for very large systems, but also that the length of time series data needed to train our multiple, parallel machine learning components is dramatically less than that necessary without parallelization. Furthermore, considering cases where computational realization of the knowledge-based component does not resolve subgrid-scale processes, our scheme is able to use training data to incorporate the effect of the unresolved short-scale dynamics upon the resolved longer-scale dynamics ("subgrid-scale closure").