Stabilizing Machine Learning Prediction of Dynamics: Noise and Noise-inspired Regularization

Recent work has shown that machine learning (ML) models can be trained to accurately forecast the dynamics of unknown chaotic dynamical systems. Such ML models can be used to produce both short-term predictions of the state evolution and long-term predictions of the statistical patterns of the dynamics (``climate''). Both of these tasks can be accomplished by employing a feedback loop, whereby the model is trained to predict forward one time step, then the trained model is iterated for multiple time steps with its output used as the input. In the absence of mitigating techniques, however, this technique can result in artificially rapid error growth, leading to inaccurate predictions and/or climate instability. In this article, we systematically examine the technique of adding noise to the ML model input during training as a means to promote stability and improve prediction accuracy. Furthermore, we introduce Linearized Multi-Noise Training (LMNT), a regularization technique that deterministically approximates the effect of many small, independent noise realizations added to the model input during training. Our case study uses reservoir computing, a machine-learning method using recurrent neural networks, to predict the spatiotemporal chaotic Kuramoto-Sivashinsky equation. We find that reservoir computers trained with noise or with LMNT produce climate predictions that appear to be indefinitely stable and have a climate very similar to the true system, while reservoir computers trained without regularization are unstable. Compared with other types of regularization that yield stability in some cases, we find that both short-term and climate predictions from reservoir computers trained with noise or with LMNT are substantially more accurate. Finally, we show that the deterministic aspect of our LMNT regularization facilitates fast hyperparameter tuning when compared to training with noise.

Using Data Assimilation to Train a Hybrid Forecast System that Combines Machine-Learning and Knowledge-Based Components

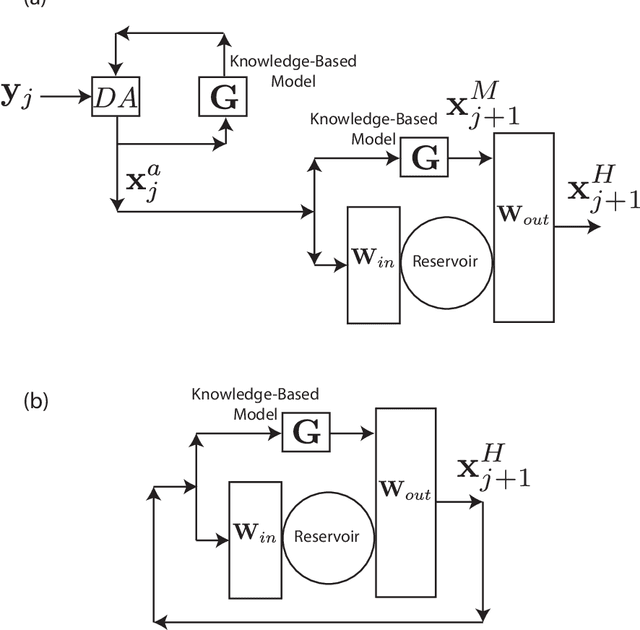
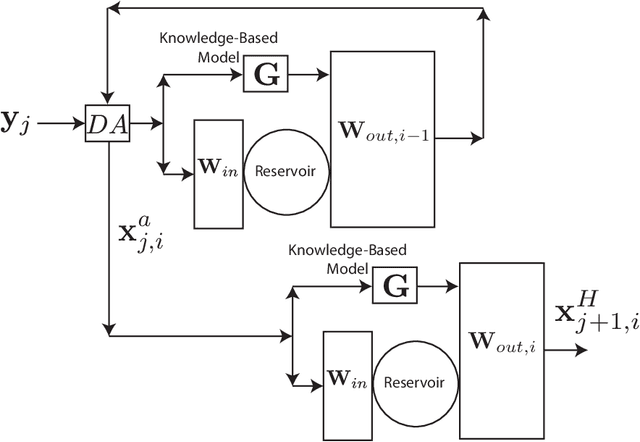
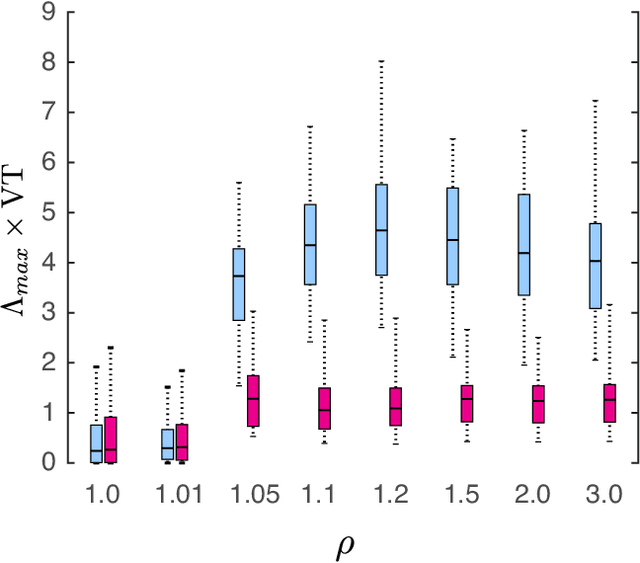
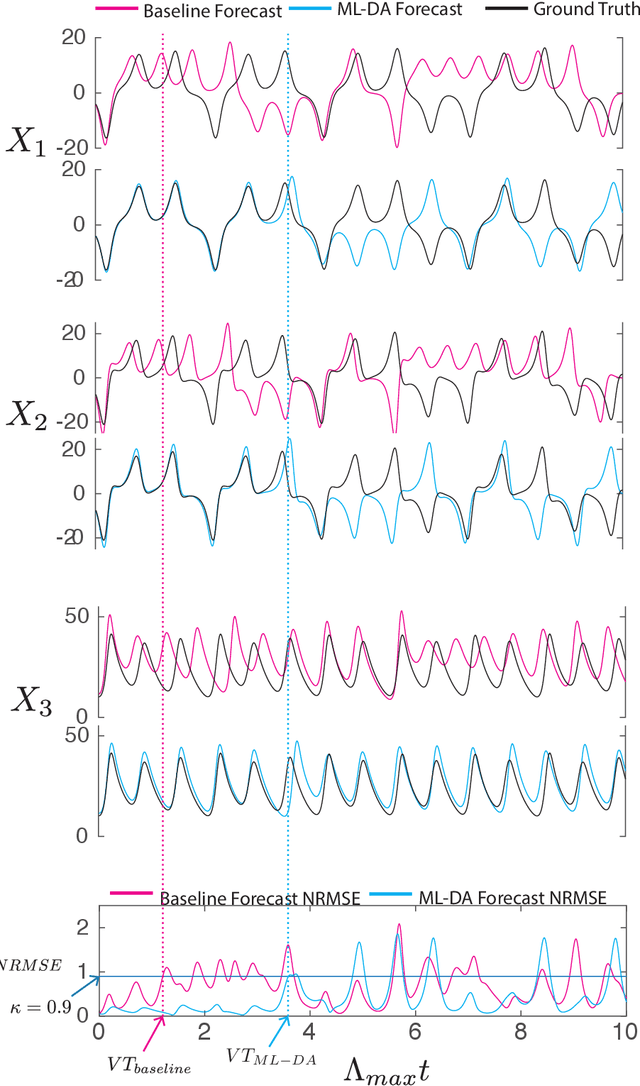
We consider the problem of data-assisted forecasting of chaotic dynamical systems when the available data is in the form of noisy partial measurements of the past and present state of the dynamical system. Recently there have been several promising data-driven approaches to forecasting of chaotic dynamical systems using machine learning. Particularly promising among these are hybrid approaches that combine machine learning with a knowledge-based model, where a machine-learning technique is used to correct the imperfections in the knowledge-based model. Such imperfections may be due to incomplete understanding and/or limited resolution of the physical processes in the underlying dynamical system, e.g., the atmosphere or the ocean. Previously proposed data-driven forecasting approaches tend to require, for training, measurements of all the variables that are intended to be forecast. We describe a way to relax this assumption by combining data assimilation with machine learning. We demonstrate this technique using the Ensemble Transform Kalman Filter (ETKF) to assimilate synthetic data for the 3-variable Lorenz system and for the Kuramoto-Sivashinsky system, simulating model error in each case by a misspecified parameter value. We show that by using partial measurements of the state of the dynamical system, we can train a machine learning model to improve predictions made by an imperfect knowledge-based model.

Forecasting of Spatio-temporal Chaotic Dynamics with Recurrent Neural Networks: a comparative study of Reservoir Computing and Backpropagation Algorithms

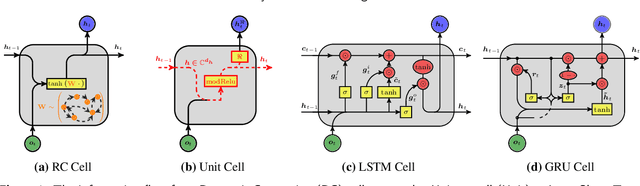
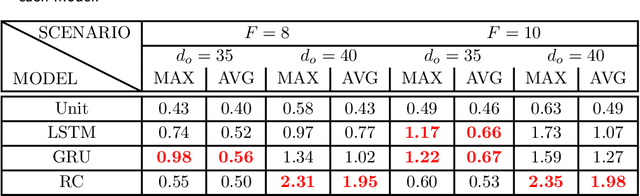
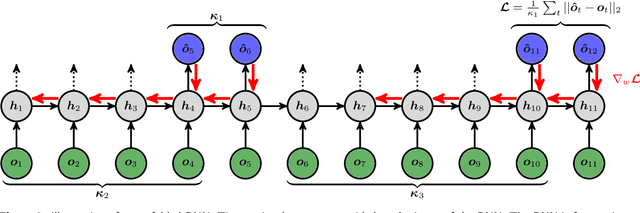
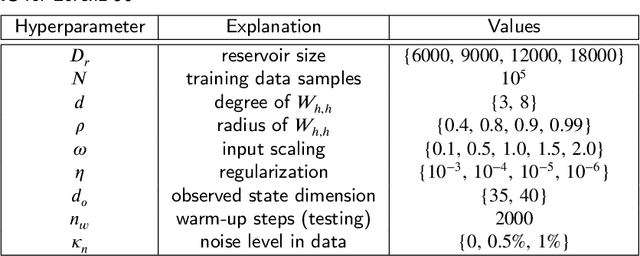
How effective are Recurrent Neural Networks (RNNs) in forecasting the spatiotemporal dynamics of chaotic systems ? We address this question through a comparative study of Reservoir Computing (RC) and backpropagation through time (BPTT) algorithms for gated network architectures on a number of benchmark problems. We quantify their relative prediction accuracy on the long-term forecasting of Lorenz-96 and the Kuramoto-Sivashinsky equation and calculation of its Lyapunov spectrum. We discuss their implementation on parallel computers and highlight advantages and limitations of each method. We find that, when the full state dynamics are available for training, RC outperforms BPTT approaches in terms of predictive performance and capturing of the long-term statistics, while at the same time requiring much less time for training. However, in the case of reduced order data, large RC models can be unstable and more likely, than the BPTT algorithms, to diverge in the long term. In contrast, RNNs trained via BPTT capture well the dynamics of these reduced order models. This study confirms that RNNs present a potent computational framework for the forecasting of complex spatio-temporal dynamics.