Forecasting of Spatio-temporal Chaotic Dynamics with Recurrent Neural Networks: a comparative study of Reservoir Computing and Backpropagation Algorithms

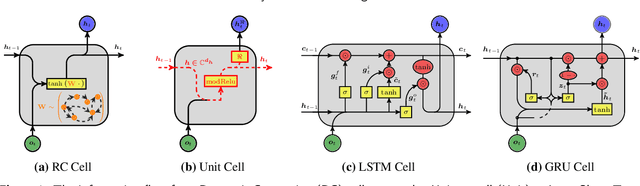
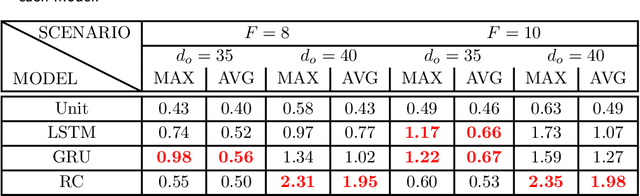
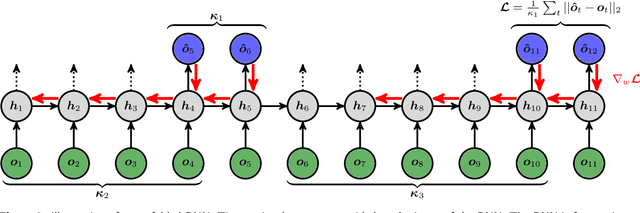
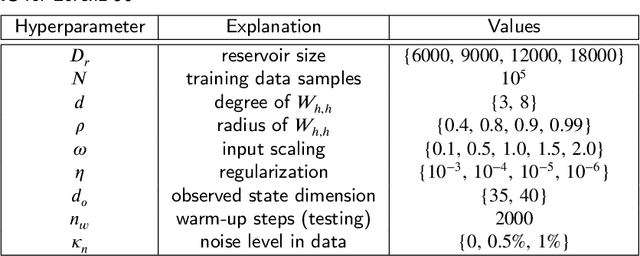
How effective are Recurrent Neural Networks (RNNs) in forecasting the spatiotemporal dynamics of chaotic systems ? We address this question through a comparative study of Reservoir Computing (RC) and backpropagation through time (BPTT) algorithms for gated network architectures on a number of benchmark problems. We quantify their relative prediction accuracy on the long-term forecasting of Lorenz-96 and the Kuramoto-Sivashinsky equation and calculation of its Lyapunov spectrum. We discuss their implementation on parallel computers and highlight advantages and limitations of each method. We find that, when the full state dynamics are available for training, RC outperforms BPTT approaches in terms of predictive performance and capturing of the long-term statistics, while at the same time requiring much less time for training. However, in the case of reduced order data, large RC models can be unstable and more likely, than the BPTT algorithms, to diverge in the long term. In contrast, RNNs trained via BPTT capture well the dynamics of these reduced order models. This study confirms that RNNs present a potent computational framework for the forecasting of complex spatio-temporal dynamics.