A Meta-learning Approach to Reservoir Computing: Time Series Prediction with Limited Data
Paper and Code
Oct 07, 2021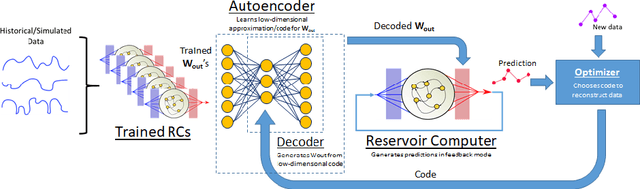
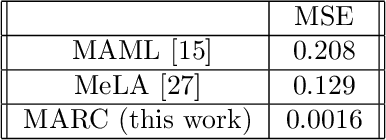
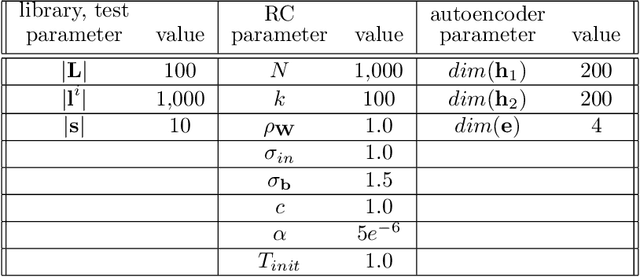
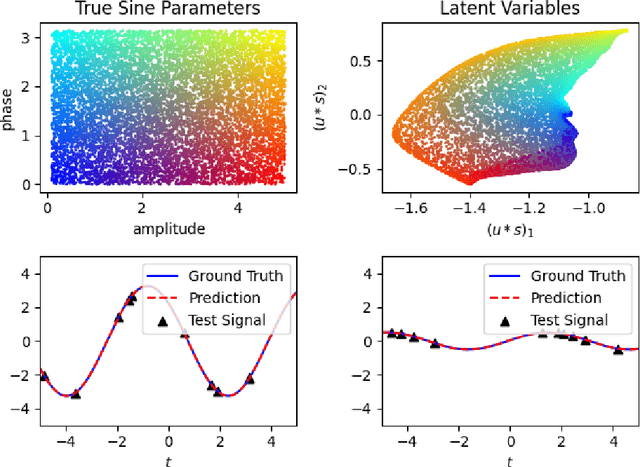
Recent research has established the effectiveness of machine learning for data-driven prediction of the future evolution of unknown dynamical systems, including chaotic systems. However, these approaches require large amounts of measured time series data from the process to be predicted. When only limited data is available, forecasters are forced to impose significant model structure that may or may not accurately represent the process of interest. In this work, we present a Meta-learning Approach to Reservoir Computing (MARC), a data-driven approach to automatically extract an appropriate model structure from experimentally observed "related" processes that can be used to vastly reduce the amount of data required to successfully train a predictive model. We demonstrate our approach on a simple benchmark problem, where it beats the state of the art meta-learning techniques, as well as a challenging chaotic problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge