A Meta-learning Approach to Reservoir Computing: Time Series Prediction with Limited Data

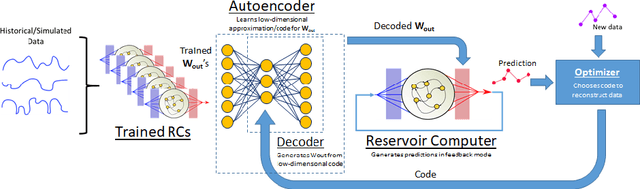
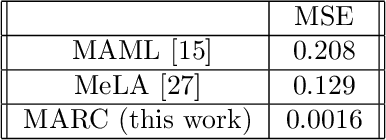
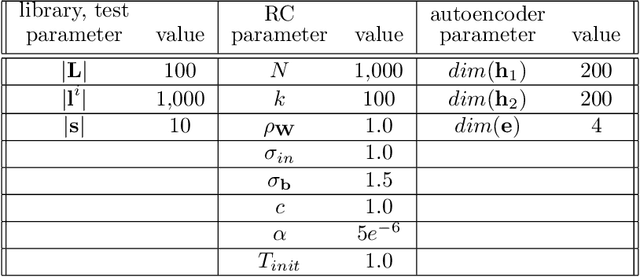
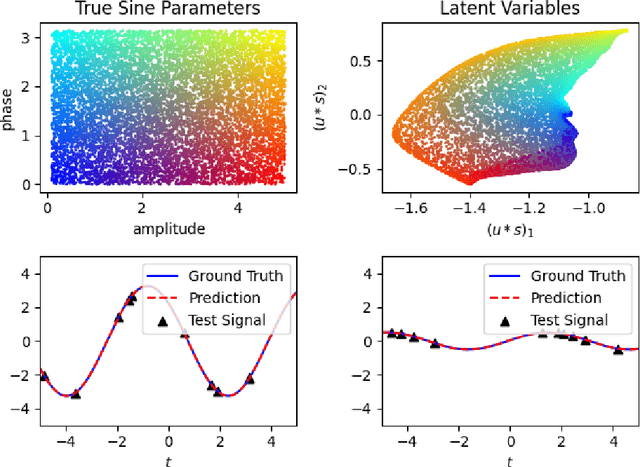
Recent research has established the effectiveness of machine learning for data-driven prediction of the future evolution of unknown dynamical systems, including chaotic systems. However, these approaches require large amounts of measured time series data from the process to be predicted. When only limited data is available, forecasters are forced to impose significant model structure that may or may not accurately represent the process of interest. In this work, we present a Meta-learning Approach to Reservoir Computing (MARC), a data-driven approach to automatically extract an appropriate model structure from experimentally observed "related" processes that can be used to vastly reduce the amount of data required to successfully train a predictive model. We demonstrate our approach on a simple benchmark problem, where it beats the state of the art meta-learning techniques, as well as a challenging chaotic problem.

Model-Free Control of Dynamical Systems with Deep Reservoir Computing

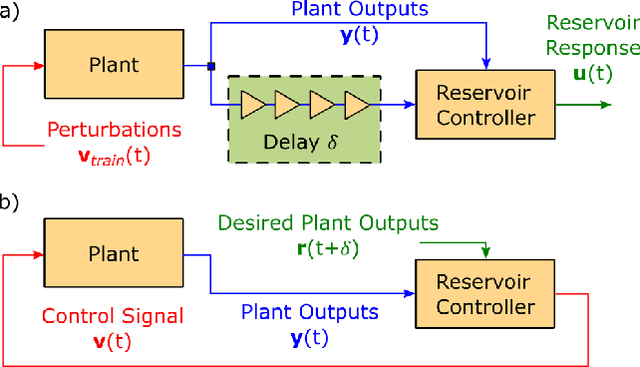
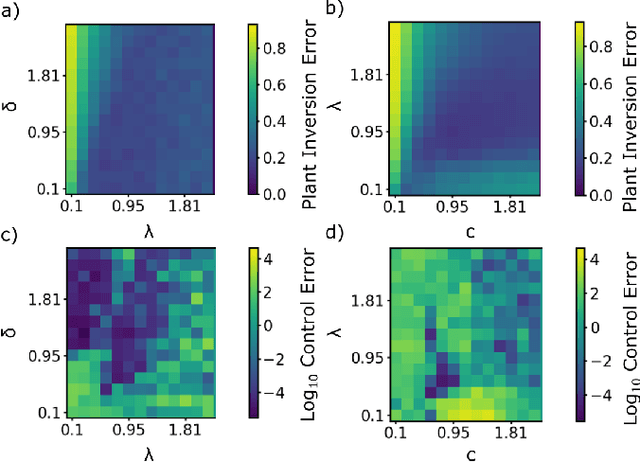
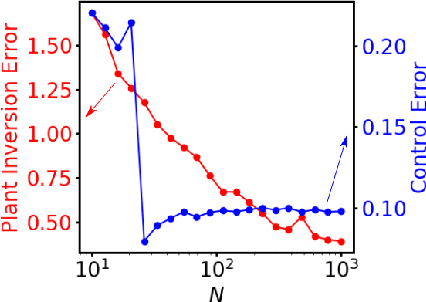
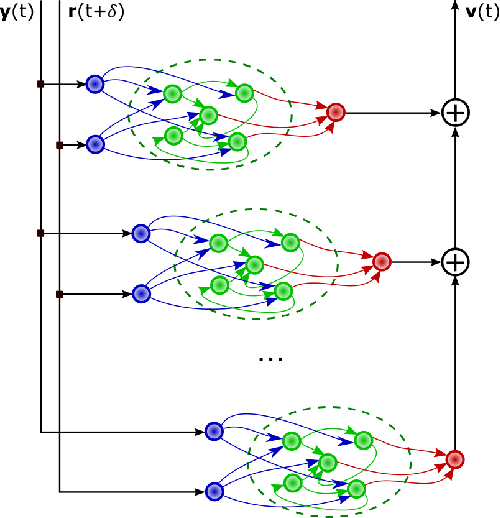
We propose and demonstrate a nonlinear control method that can be applied to unknown, complex systems where the controller is based on a type of artificial neural network known as a reservoir computer. In contrast to many modern neural-network-based control techniques, which are robust to system uncertainties but require a model nonetheless, our technique requires no prior knowledge of the system and is thus model-free. Further, our approach does not require an initial system identification step, resulting in a relatively simple and efficient learning process. Reservoir computers are well-suited to the control problem because they require small training data sets and remarkably low training times. By iteratively training and adding layers of reservoir computers to the controller, a precise and efficient control law is identified quickly. With examples on both numerical and high-speed experimental systems, we demonstrate that our approach is capable of controlling highly complex dynamical systems that display deterministic chaos to nontrivial target trajectories.

Rapid Time Series Prediction with a Hardware-Based Reservoir Computer

Reservoir computing is a neural network approach for processing time-dependent signals that has seen rapid development in recent years. Physical implementations of the technique using optical reservoirs have demonstrated remarkable accuracy and processing speed at benchmark tasks. However, these approaches require an electronic output layer to maintain high performance, which limits their use in tasks such as time-series prediction, where the output is fed back into the reservoir. We present here a reservoir computing scheme that has rapid processing speed both by the reservoir and the output layer. The reservoir is realized by an autonomous, time-delay, Boolean network configured on a field-programmable gate array. We investigate the dynamical properties of the network and observe the fading memory property that is critical for successful reservoir computing. We demonstrate the utility of the technique by training a reservoir to learn the short- and long-term behavior of a chaotic system. We find accuracy comparable to state-of-the-art software approaches of similar network size, but with a superior real-time prediction rate up to 160 MHz.