Next Generation Reservoir Computing

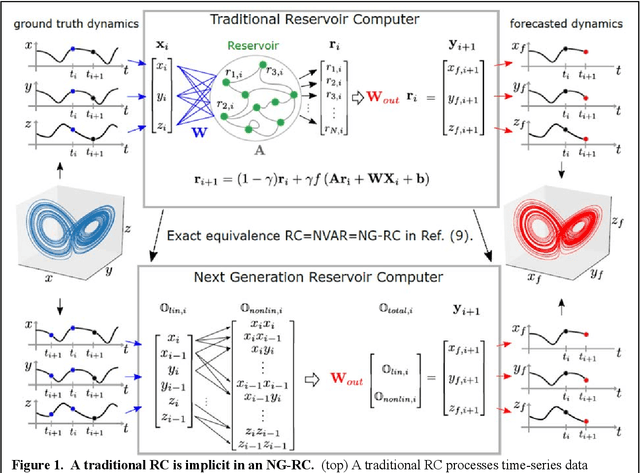
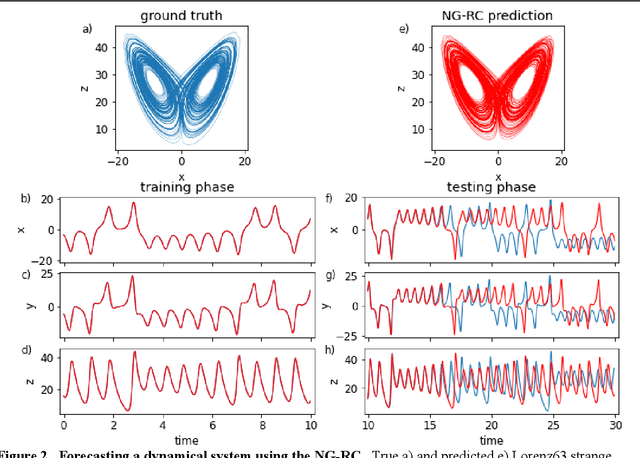
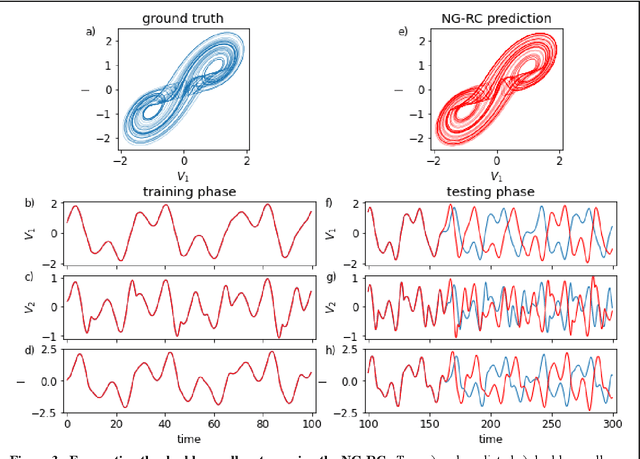
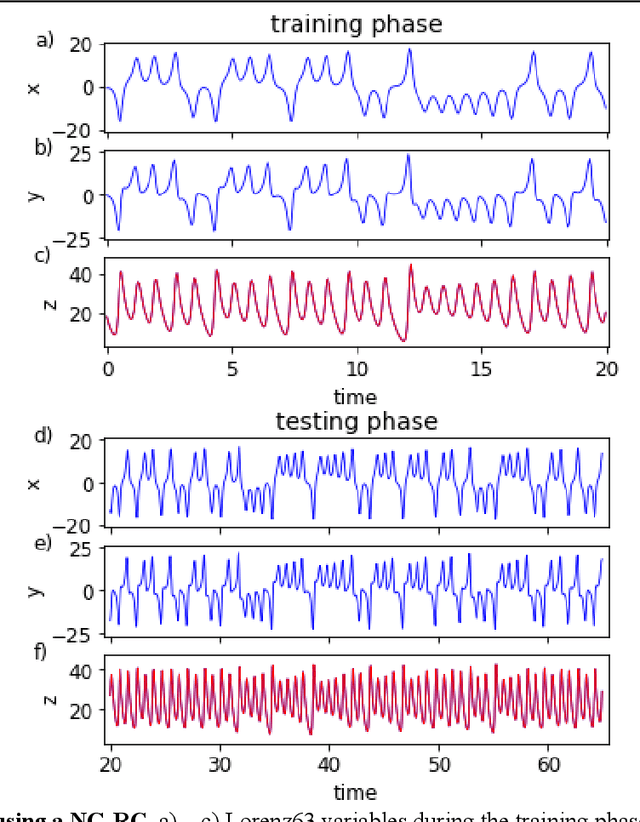
Reservoir computing is a best-in-class machine learning algorithm for processing information generated by dynamical systems using observed time-series data. Importantly, it requires very small training data sets, uses linear optimization, and thus requires minimal computing resources. However, the algorithm uses randomly sampled matrices to define the underlying recurrent neural network and has a multitude of metaparameters that must be optimized. Recent results demonstrate the equivalence of reservoir computing to nonlinear vector autoregression, which requires no random matrices, fewer metaparameters, and provides interpretable results. Here, we demonstrate that nonlinear vector autoregression excels at reservoir computing benchmark tasks and requires even shorter training data sets and training time, heralding the next generation of reservoir computing.

Symmetry-Aware Reservoir Computing

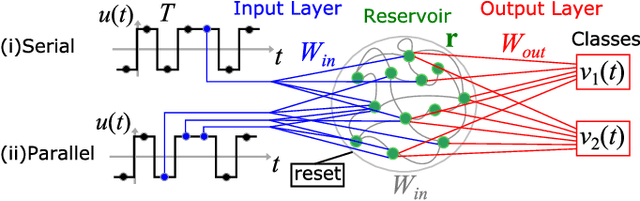
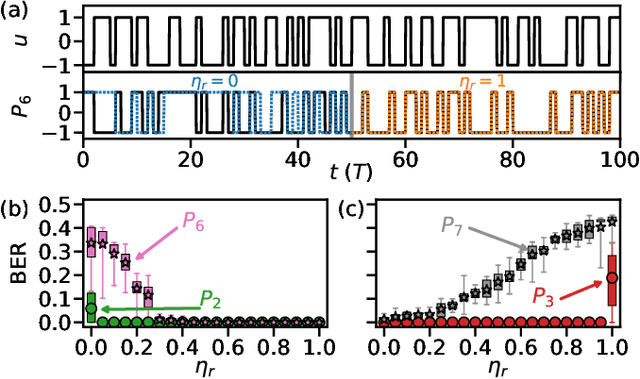
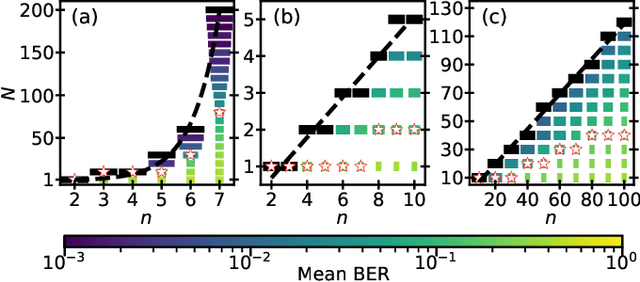
We demonstrate that matching the symmetry properties of a reservoir computer (RC) to the data being processed can dramatically increase its processing power. We apply our method to the parity task, a challenging benchmark problem, which highlights the benefits of symmetry matching. Our method outperforms all other approaches on this task, even artificial neural networks (ANN) hand crafted for this problem. The symmetry-aware RC can obtain zero error using an exponentially reduced number of artificial neurons and training data, greatly speeding up the time-to-result. We anticipate that generalizations of our procedure will have widespread applicability in information processing with ANNs.

Forecasting Chaotic Systems with Very Low Connectivity Reservoir Computers

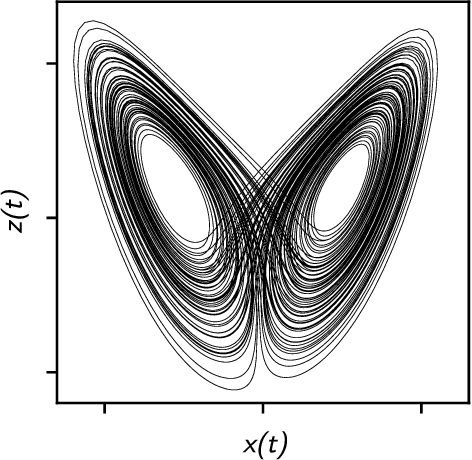
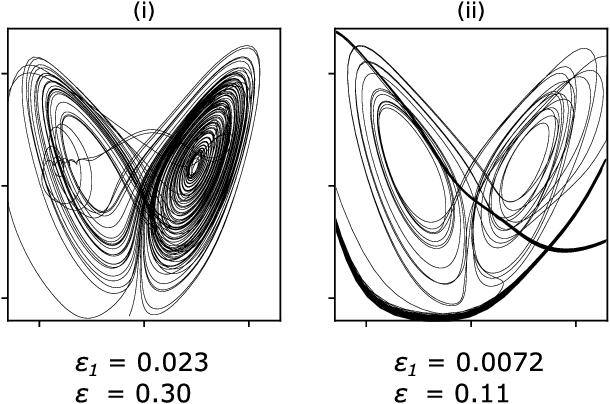
We explore the hyperparameter space of reservoir computers used for forecasting of the chaotic Lorenz '63 attractor with Bayesian optimization. We use a new measure of reservoir performance, designed to emphasize learning the global climate of the forecasted system rather than short-term prediction. We find that optimizing over this measure more quickly excludes reservoirs that fail to reproduce the climate. The results of optimization are surprising: the optimized parameters often specify a reservoir network with very low connectivity. Inspired by this observation, we explore reservoir designs with even simpler structure, and find well-performing reservoirs that have zero spectral radius and no recurrence. These simple reservoirs provide counterexamples to widely used heuristics in the field, and may be useful for hardware implementations of reservoir computers.

Rapid Time Series Prediction with a Hardware-Based Reservoir Computer

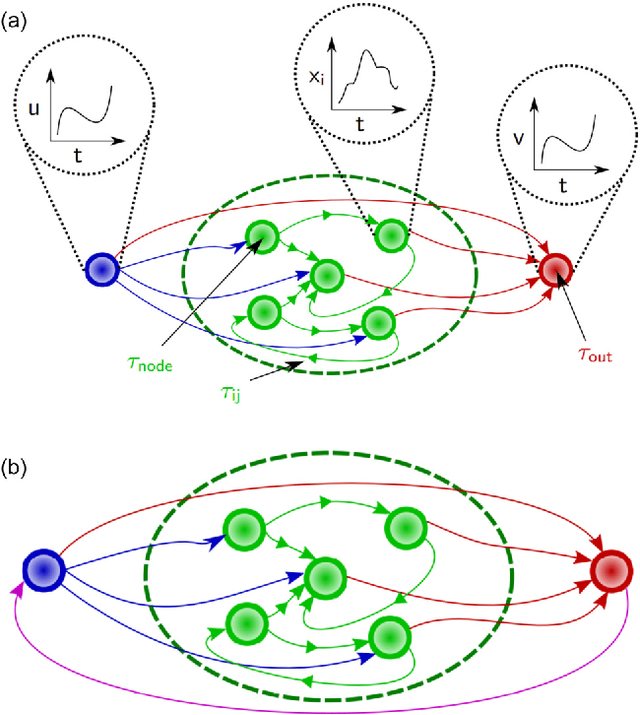
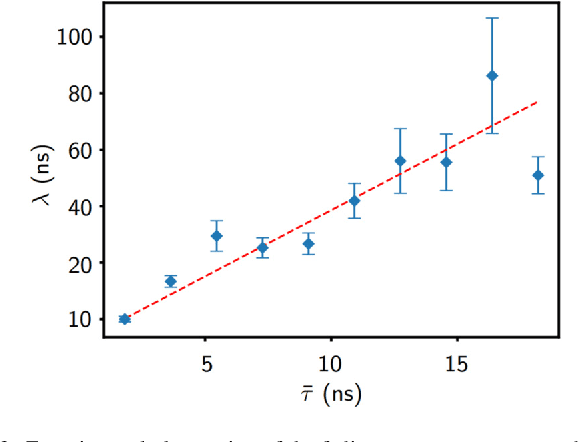
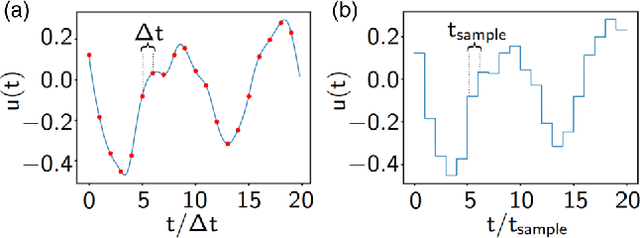
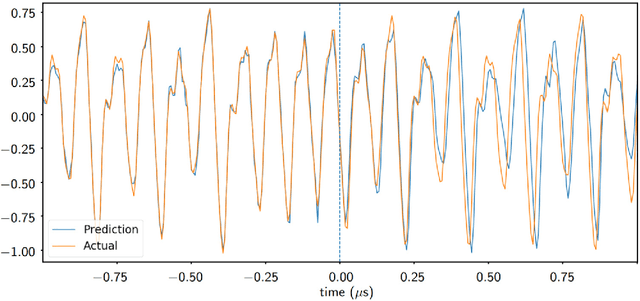
Reservoir computing is a neural network approach for processing time-dependent signals that has seen rapid development in recent years. Physical implementations of the technique using optical reservoirs have demonstrated remarkable accuracy and processing speed at benchmark tasks. However, these approaches require an electronic output layer to maintain high performance, which limits their use in tasks such as time-series prediction, where the output is fed back into the reservoir. We present here a reservoir computing scheme that has rapid processing speed both by the reservoir and the output layer. The reservoir is realized by an autonomous, time-delay, Boolean network configured on a field-programmable gate array. We investigate the dynamical properties of the network and observe the fading memory property that is critical for successful reservoir computing. We demonstrate the utility of the technique by training a reservoir to learn the short- and long-term behavior of a chaotic system. We find accuracy comparable to state-of-the-art software approaches of similar network size, but with a superior real-time prediction rate up to 160 MHz.