Indoor Occupancy Classification using a Compact Hybrid Quantum-Classical Model Enabled by a Physics-Informed Radar Digital Twin

Indoor occupancy classification enables privacy-preserving monitoring in settings such as remote elder care, where presence information helps triage alarms without cameras or wearables. Radar suits this role by sensing motion through occlusions and in darkness. Modern deep-learning pipelines are the standard for interpreting radar returns effectively; however, they are often parameter-heavy and sensitive at low signal-to-noise ratios (SNR), motivating compact alternatives like Hybrid Quantum Neural Networks (HQNNs). A two-qubit HQNN is benchmarked against convolutional neural networks (CNNs) using a physics-informed 60GHz digital twin and real radar measurements under matched training protocols. In clean conditions, the HQNN achieves high accuracy (99.7% synthetic; 97.0% real) with up to 170x fewer parameters (0.066M). Its parameter efficiency is shown to be structural, as an ablation of the parameterized quantum circuit (PQC) causes sharp performance drops on real data (to 68.5% and 31.5% for the control heads). A domain-dependent sensitivity emerges under additive-noise evaluation, where the HQNN begins recovery earlier in synthetic data while CNNs recover more steeply and peak higher on real measurements. In label-fraction ablations, CNNs prove more sample-efficient on real Range-Doppler Maps (RDMs), with the performance gap being most pronounced (at 50% labels, BA 0.89-0.99 vs. HQNN 0.75). On synthetic data, this gap narrows significantly, largely vanishing by the 50% label mark. Overall, the HQNN's value lies in parameter efficiency and a compact inductive bias that shapes its distinct sensitivity profile; this work establishes a rigorous baseline for hybrid quantum models in privacy-preserving radar occupancy sensing.

Reservoir Computing with Superconducting Electronics

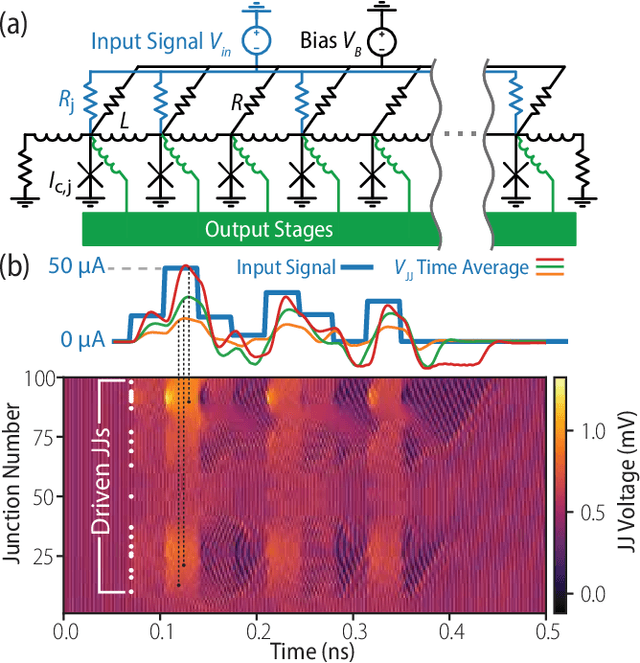
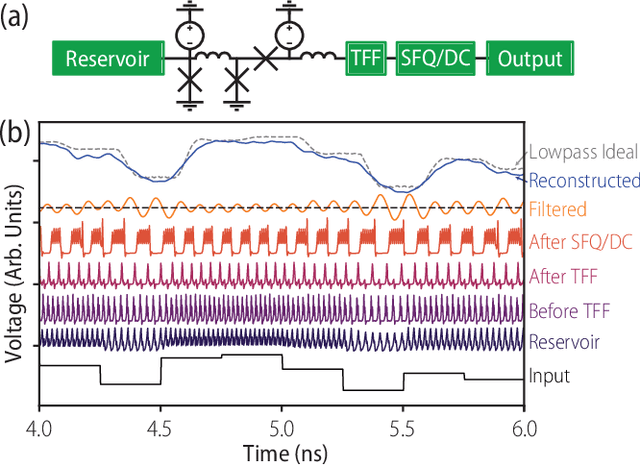
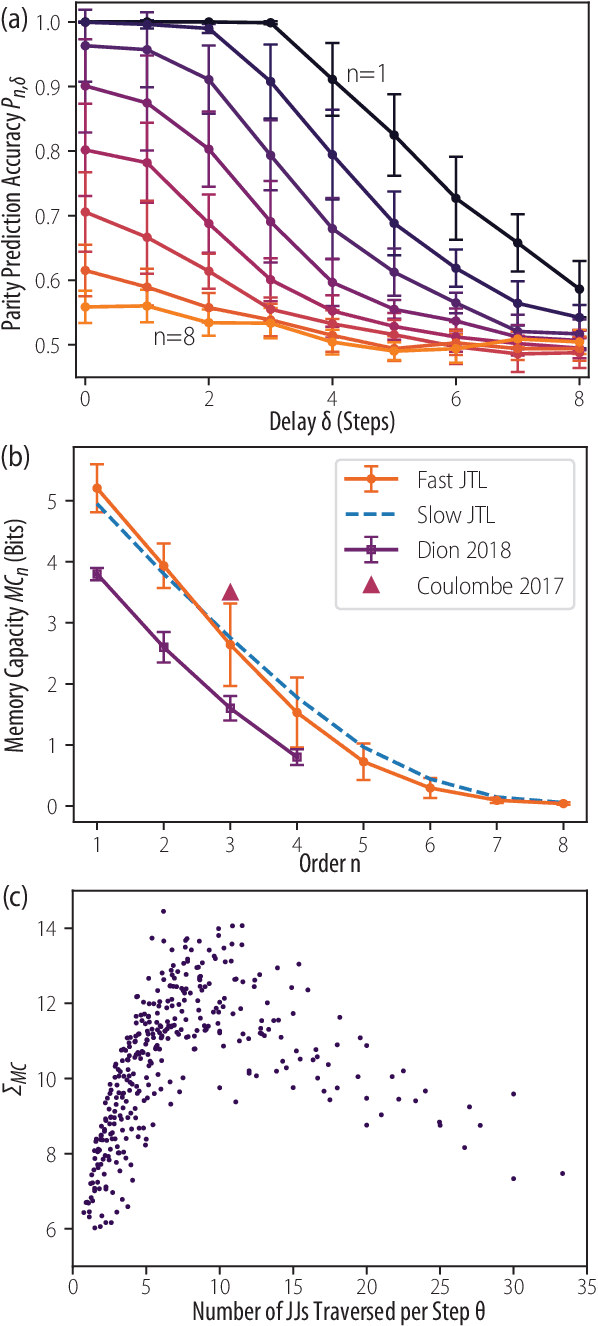
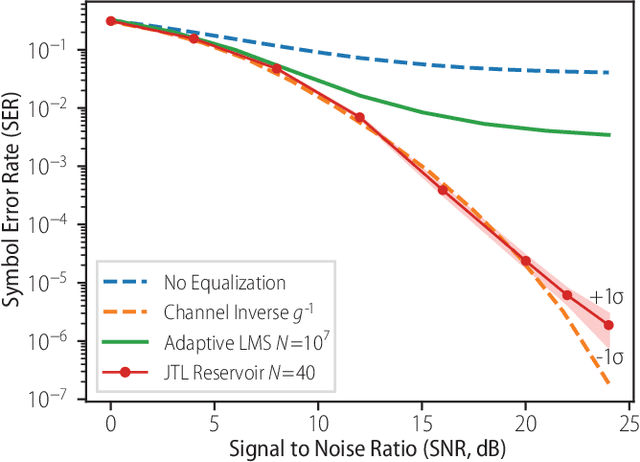
The rapidity and low power consumption of superconducting electronics makes them an ideal substrate for physical reservoir computing, which commandeers the computational power inherent to the evolution of a dynamical system for the purposes of performing machine learning tasks. We focus on a subset of superconducting circuits that exhibit soliton-like dynamics in simple transmission line geometries. With numerical simulations we demonstrate the effectiveness of these circuits in performing higher-order parity calculations and channel equalization at rates approaching 100 Gb/s. The availability of a proven superconducting logic scheme considerably simplifies the path to a fully integrated reservoir computing platform and makes superconducting reservoirs an enticing substrate for high rate signal processing applications.

Symmetry-Aware Reservoir Computing

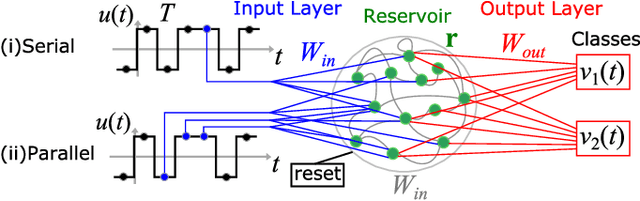
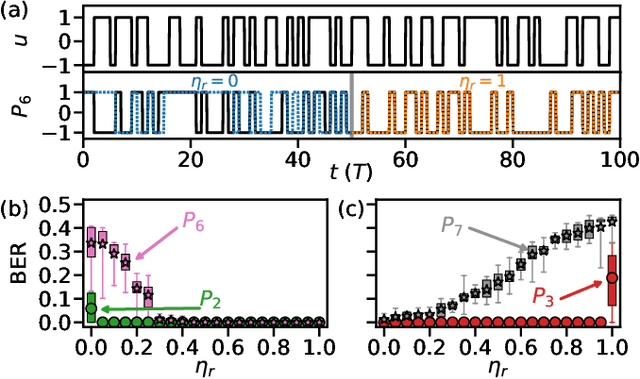
We demonstrate that matching the symmetry properties of a reservoir computer (RC) to the data being processed can dramatically increase its processing power. We apply our method to the parity task, a challenging benchmark problem, which highlights the benefits of symmetry matching. Our method outperforms all other approaches on this task, even artificial neural networks (ANN) hand crafted for this problem. The symmetry-aware RC can obtain zero error using an exponentially reduced number of artificial neurons and training data, greatly speeding up the time-to-result. We anticipate that generalizations of our procedure will have widespread applicability in information processing with ANNs.