Daniel J. Gauthier
Efficient measurement of neutral-atom qubits with matched filters
Apr 10, 2025



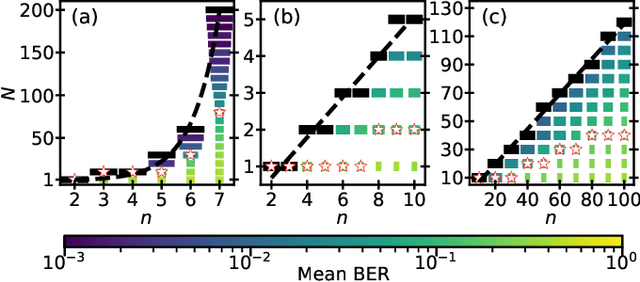
Abstract:Quantum computers require high-fidelity measurement of many qubits to achieve a quantum advantage. Traditional approaches suffer from readout crosstalk for a neutral-atom quantum processor with a tightly spaced array. Although classical machine learning algorithms based on convolutional neural networks can improve fidelity, they are computationally expensive, making it difficult to scale them to large qubit counts. We present two simpler and scalable machine learning algorithms that realize matched filters for the readout problem. One is a local model that focuses on a single qubit, and the other uses information from neighboring qubits in the array to prevent crosstalk among the qubits. We demonstrate error reductions of up to 32% and 43% for the site and array models, respectively, compared to a conventional Gaussian threshold approach. Additionally, our array model uses two orders of magnitude fewer trainable parameters and four orders of magnitude fewer multiplications and nonlinear function evaluations than a recent convolutional neural network approach, with only a minor (3.5%) increase in error across different readout times. Another strength of our approach is its physical interpretability: the learned filter can be visualized to provide insights into experimental imperfections. We also show that a convolutional neural network model for improved can be pruned to have 70x and 4000x fewer parameters, respectively, while maintaining similar errors. Our work shows that simple machine learning approaches can achieve high-fidelity qubit measurements while remaining scalable to systems with larger qubit counts.
Controlling Chaotic Maps using Next-Generation Reservoir Computing
Jul 07, 2023Abstract:In this work, we combine nonlinear system control techniques with next-generation reservoir computing, a best-in-class machine learning approach for predicting the behavior of dynamical systems. We demonstrate the performance of the controller in a series of control tasks for the chaotic H\'enon map, including controlling the system between unstable fixed-points, stabilizing the system to higher order periodic orbits, and to an arbitrary desired state. We show that our controller succeeds in these tasks, requires only 10 data points for training, can control the system to a desired trajectory in a single iteration, and is robust to noise and modeling error.
Learning unseen coexisting attractors
Jul 28, 2022



Abstract:Reservoir computing is a machine learning approach that can generate a surrogate model of a dynamical system. It can learn the underlying dynamical system using fewer trainable parameters and hence smaller training data sets than competing approaches. Recently, a simpler formulation, known as next-generation reservoir computing, removes many algorithm metaparameters and identifies a well-performing traditional reservoir computer, thus simplifying training even further. Here, we study a particularly challenging problem of learning a dynamical system that has both disparate time scales and multiple co-existing dynamical states (attractors). We compare the next-generation and traditional reservoir computer using metrics quantifying the geometry of the ground-truth and forecasted attractors. For the studied four-dimensional system, the next-generation reservoir computing approach uses $\sim 1.7 \times$ less training data, requires $10^3 \times$ shorter `warm up' time, has fewer metaparameters, and has an $\sim 100\times$ higher accuracy in predicting the co-existing attractor characteristics in comparison to a traditional reservoir computer. Furthermore, we demonstrate that it predicts the basin of attraction with high accuracy. This work lends further support to the superior learning ability of this new machine learning algorithm for dynamical systems.
Learning Spatiotemporal Chaos Using Next-Generation Reservoir Computing
Mar 24, 2022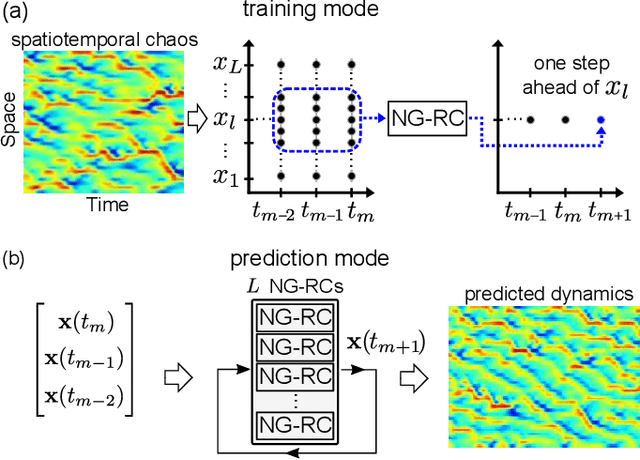
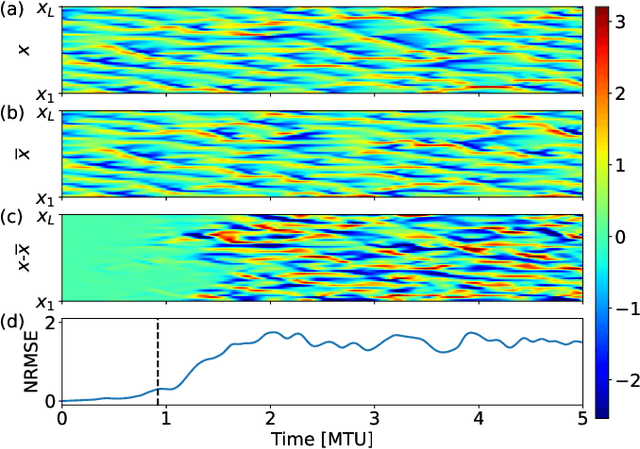
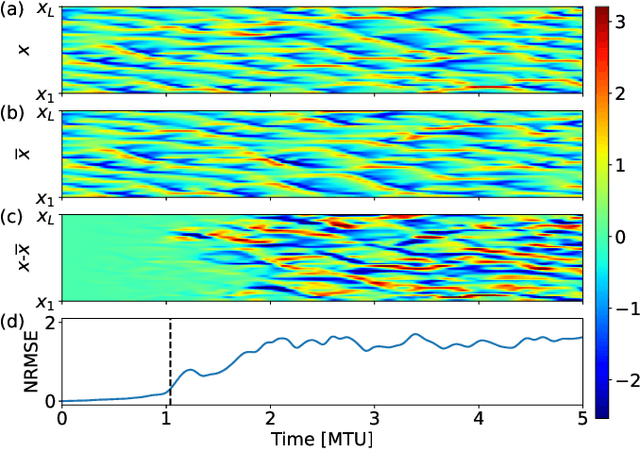
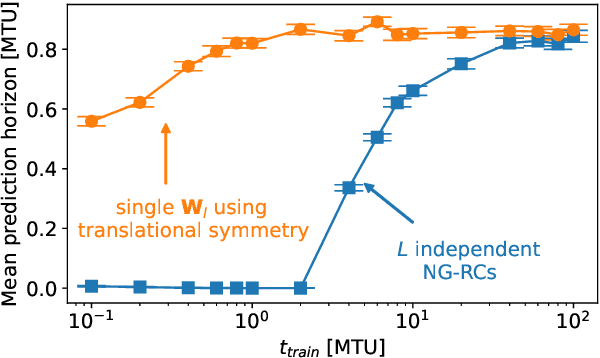
Abstract:Forecasting the behavior of high-dimensional dynamical systems using machine learning (ML) requires efficient methods to learn the underlying physical model. We demonstrate spatiotemporal chaos prediction of a heuristic atmospheric weather model using an ML architecture that, when combined with a next-generation reservoir computer, displays state-of-the-art performance with a training time $10^3-10^4$ times faster and training data set $\sim 10^2$ times smaller than other ML algorithms. We also take advantage of the translational symmetry of the model to further reduce the computational cost and training data, each by a factor of $\sim$10.
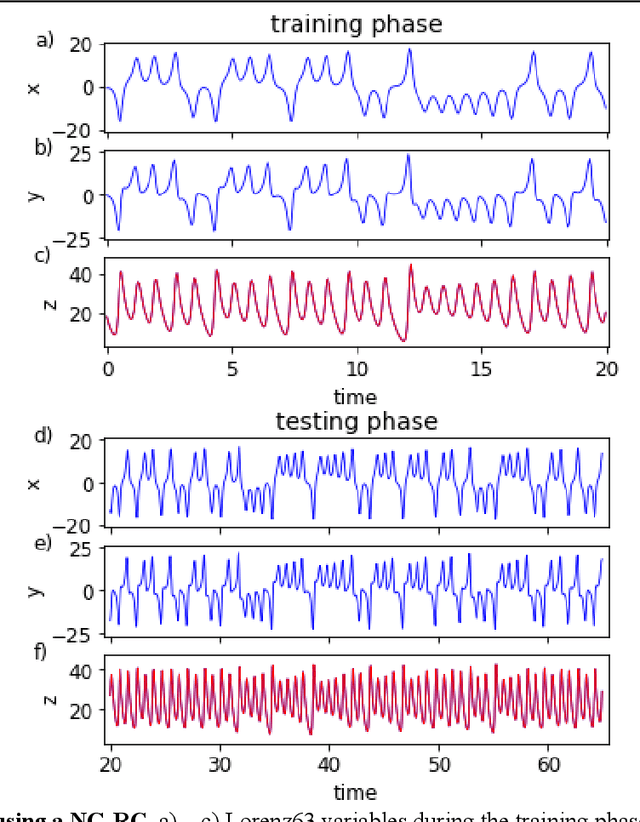
Model-free inference of unseen attractors: Reconstructing phase space features from a single noisy trajectory using reservoir computing
Aug 06, 2021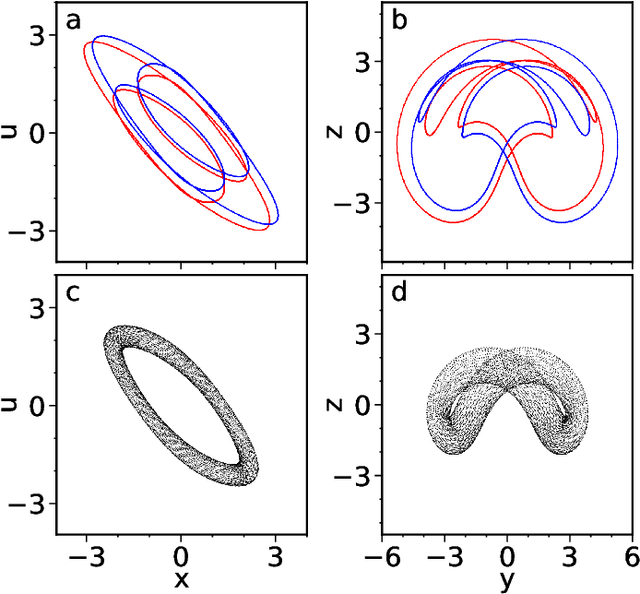
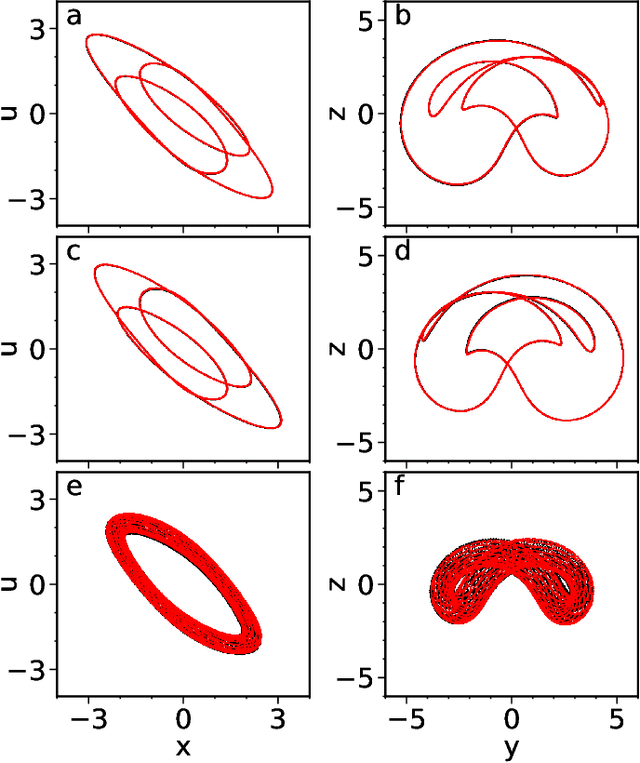


Abstract:Reservoir computers are powerful tools for chaotic time series prediction. They can be trained to approximate phase space flows and can thus both predict future values to a high accuracy, as well as reconstruct the general properties of a chaotic attractor without requiring a model. In this work, we show that the ability to learn the dynamics of a complex system can be extended to systems with co-existing attractors, here a 4-dimensional extension of the well-known Lorenz chaotic system. We demonstrate that a reservoir computer can infer entirely unexplored parts of the phase space: a properly trained reservoir computer can predict the existence of attractors that were never approached during training and therefore are labelled as unseen. We provide examples where attractor inference is achieved after training solely on a single noisy trajectory.
Next Generation Reservoir Computing
Jun 14, 2021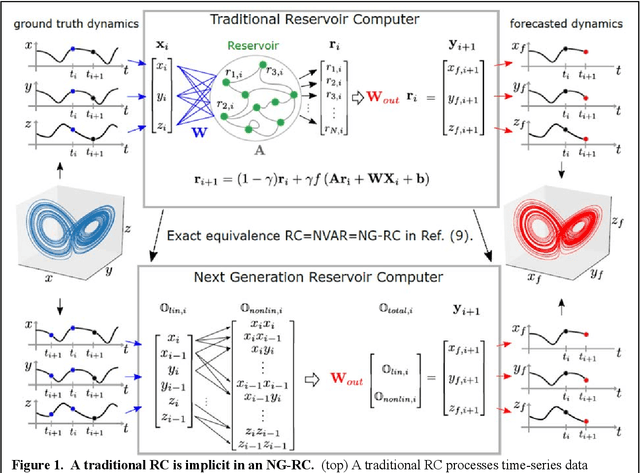
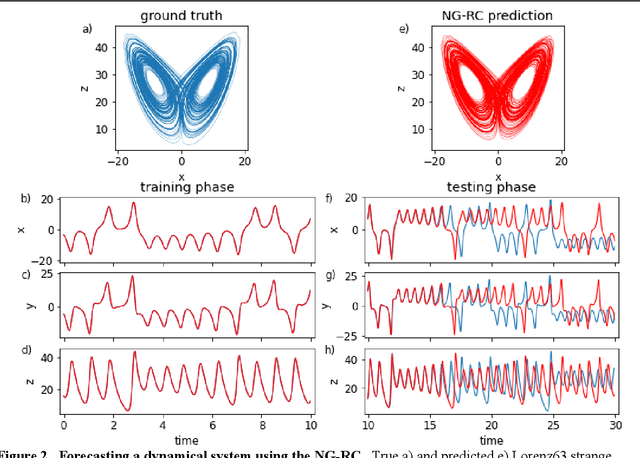
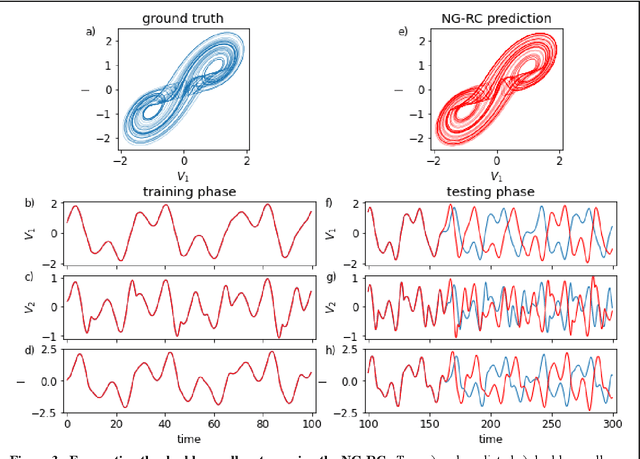
Abstract:Reservoir computing is a best-in-class machine learning algorithm for processing information generated by dynamical systems using observed time-series data. Importantly, it requires very small training data sets, uses linear optimization, and thus requires minimal computing resources. However, the algorithm uses randomly sampled matrices to define the underlying recurrent neural network and has a multitude of metaparameters that must be optimized. Recent results demonstrate the equivalence of reservoir computing to nonlinear vector autoregression, which requires no random matrices, fewer metaparameters, and provides interpretable results. Here, we demonstrate that nonlinear vector autoregression excels at reservoir computing benchmark tasks and requires even shorter training data sets and training time, heralding the next generation of reservoir computing.
Reservoir Computing with Superconducting Electronics
Mar 03, 2021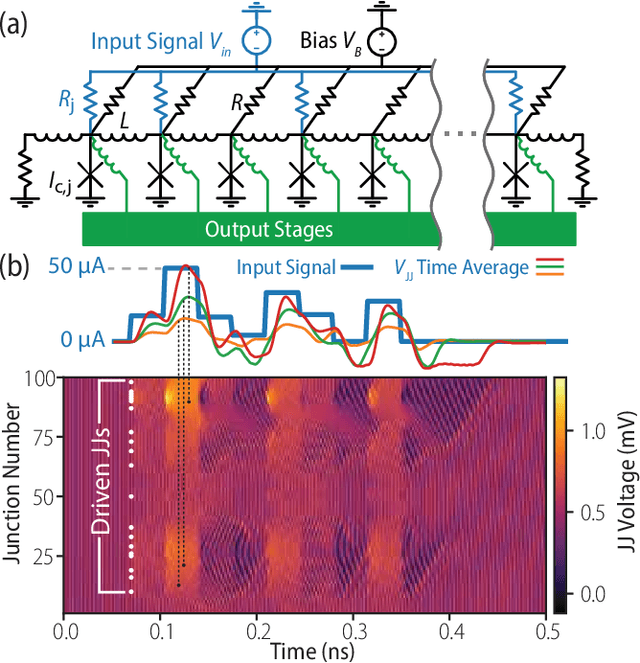
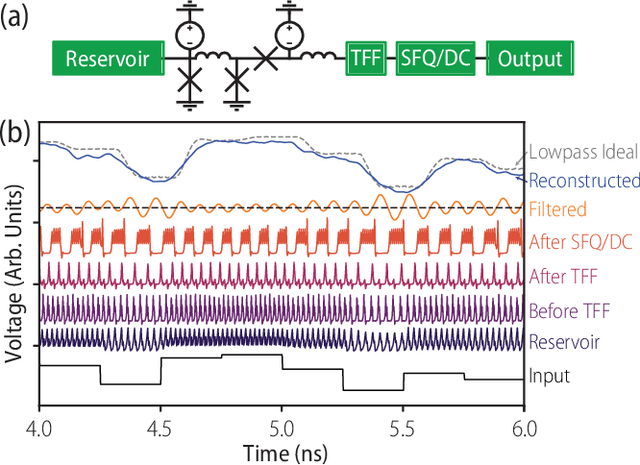
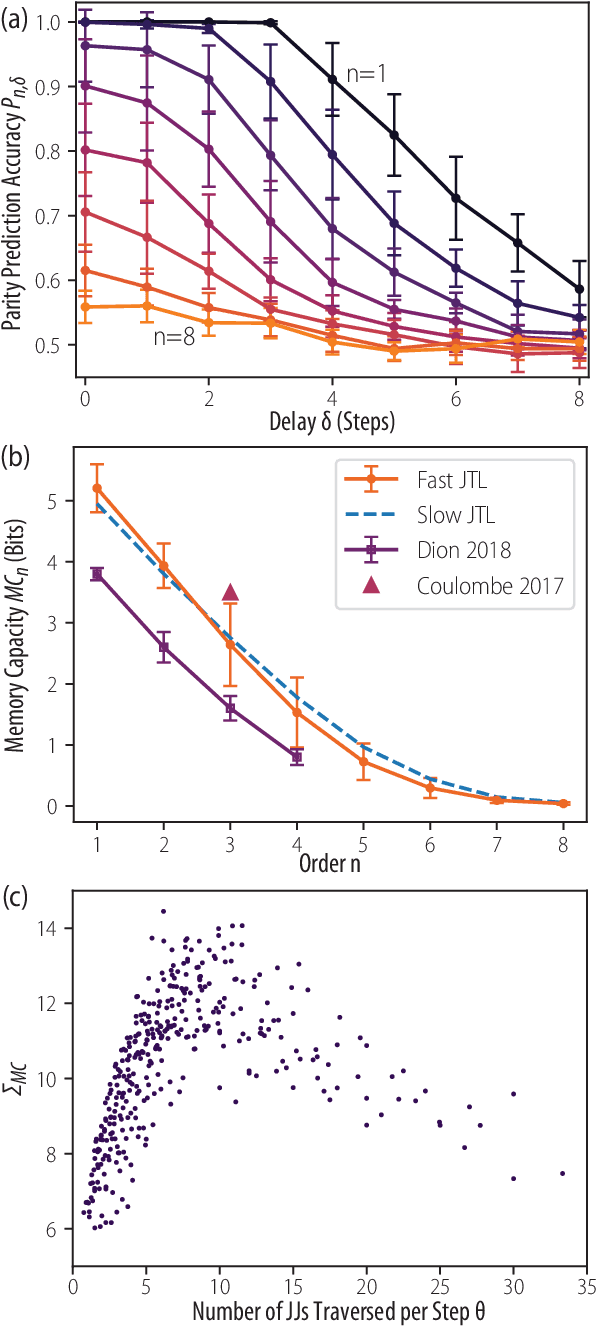
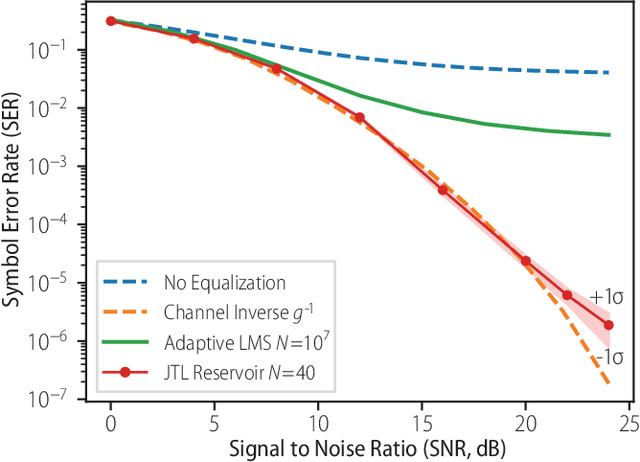
Abstract:The rapidity and low power consumption of superconducting electronics makes them an ideal substrate for physical reservoir computing, which commandeers the computational power inherent to the evolution of a dynamical system for the purposes of performing machine learning tasks. We focus on a subset of superconducting circuits that exhibit soliton-like dynamics in simple transmission line geometries. With numerical simulations we demonstrate the effectiveness of these circuits in performing higher-order parity calculations and channel equalization at rates approaching 100 Gb/s. The availability of a proven superconducting logic scheme considerably simplifies the path to a fully integrated reservoir computing platform and makes superconducting reservoirs an enticing substrate for high rate signal processing applications.
Symmetry-Aware Reservoir Computing
Jan 30, 2021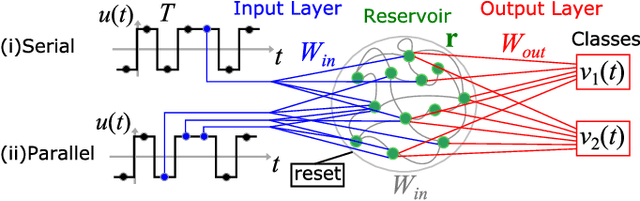
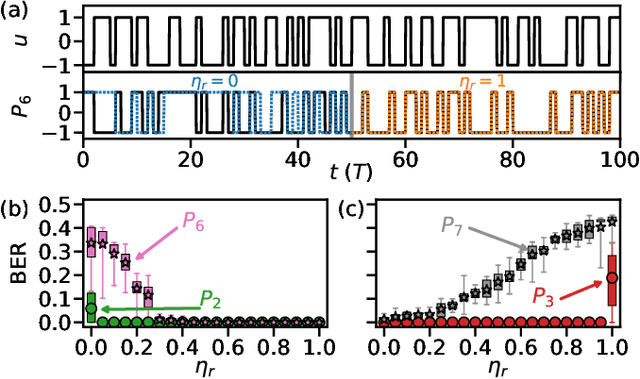
Abstract:We demonstrate that matching the symmetry properties of a reservoir computer (RC) to the data being processed can dramatically increase its processing power. We apply our method to the parity task, a challenging benchmark problem, which highlights the benefits of symmetry matching. Our method outperforms all other approaches on this task, even artificial neural networks (ANN) hand crafted for this problem. The symmetry-aware RC can obtain zero error using an exponentially reduced number of artificial neurons and training data, greatly speeding up the time-to-result. We anticipate that generalizations of our procedure will have widespread applicability in information processing with ANNs.
Forecasting Chaotic Systems with Very Low Connectivity Reservoir Computers
Oct 01, 2019
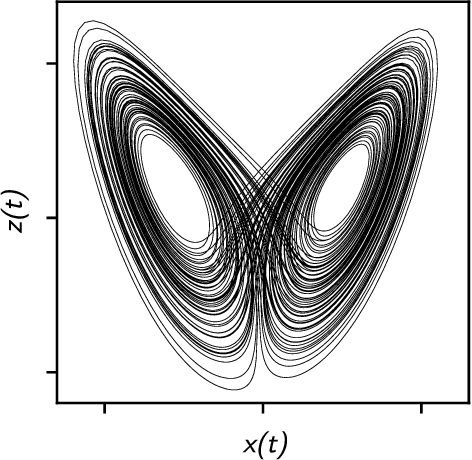

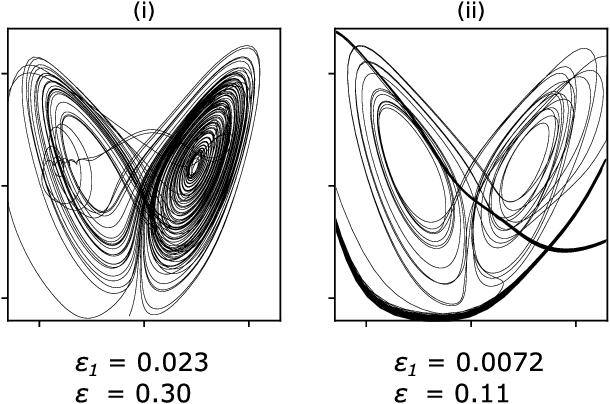
Abstract:We explore the hyperparameter space of reservoir computers used for forecasting of the chaotic Lorenz '63 attractor with Bayesian optimization. We use a new measure of reservoir performance, designed to emphasize learning the global climate of the forecasted system rather than short-term prediction. We find that optimizing over this measure more quickly excludes reservoirs that fail to reproduce the climate. The results of optimization are surprising: the optimized parameters often specify a reservoir network with very low connectivity. Inspired by this observation, we explore reservoir designs with even simpler structure, and find well-performing reservoirs that have zero spectral radius and no recurrence. These simple reservoirs provide counterexamples to widely used heuristics in the field, and may be useful for hardware implementations of reservoir computers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge