Adaptive control of recurrent neural networks using conceptors

Recurrent Neural Networks excel at predicting and generating complex high-dimensional temporal patterns. Due to their inherent nonlinear dynamics and memory, they can learn unbounded temporal dependencies from data. In a Machine Learning setting, the network's parameters are adapted during a training phase to match the requirements of a given task/problem increasing its computational capabilities. After the training, the network parameters are kept fixed to exploit the learned computations. The static parameters thereby render the network unadaptive to changing conditions, such as external or internal perturbation. In this manuscript, we demonstrate how keeping parts of the network adaptive even after the training enhances its functionality and robustness. Here, we utilize the conceptor framework and conceptualize an adaptive control loop analyzing the network's behavior continuously and adjusting its time-varying internal representation to follow a desired target. We demonstrate how the added adaptivity of the network supports the computational functionality in three distinct tasks: interpolation of temporal patterns, stabilization against partial network degradation, and robustness against input distortion. Our results highlight the potential of adaptive networks in machine learning beyond training, enabling them to not only learn complex patterns but also dynamically adjust to changing environments, ultimately broadening their applicability.

Experimental demonstration of bandwidth enhancement in photonic time delay reservoir computing

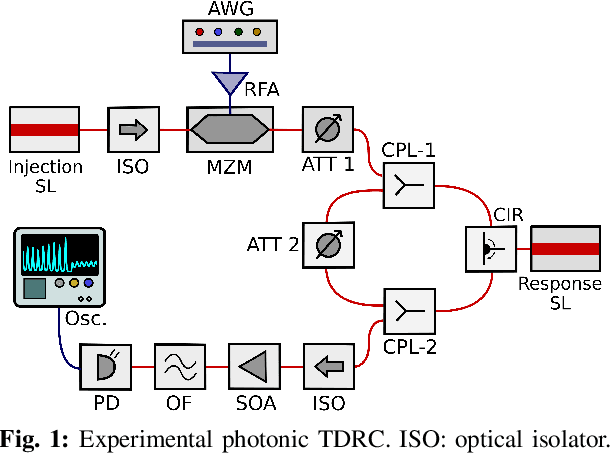
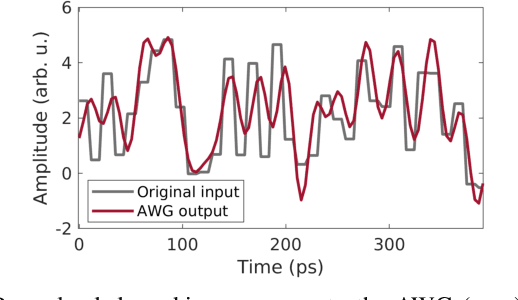
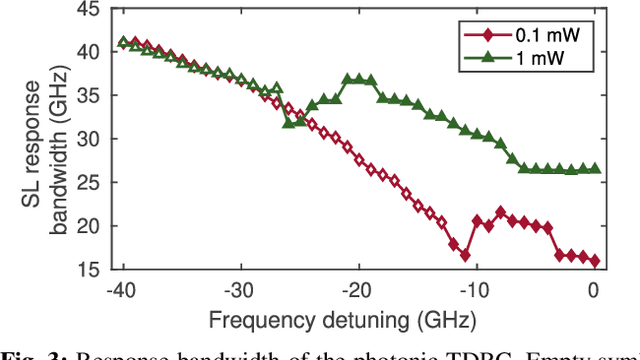
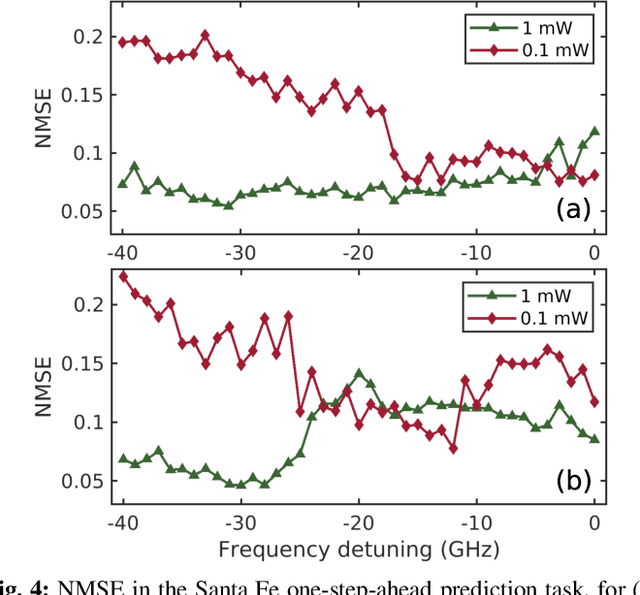
Time delay reservoir computing (TDRC) using semiconductor lasers (SLs) has proven to be a promising photonic analog approach for information processing. One appealing property is that SLs subject to delayed optical feedback and external optical injection, allow tuning the response bandwidth by changing the level of optical injection. Here we use strong optical injection, thereby expanding the SL's modulation response up to tens of GHz. Performing a nonlinear time series prediction task, we demonstrate experimentally that for appropriate operating conditions, our TDRC system can operate with sampling times as small as 11.72 ps, without sacrificing computational performance.

Learning unseen coexisting attractors

Reservoir computing is a machine learning approach that can generate a surrogate model of a dynamical system. It can learn the underlying dynamical system using fewer trainable parameters and hence smaller training data sets than competing approaches. Recently, a simpler formulation, known as next-generation reservoir computing, removes many algorithm metaparameters and identifies a well-performing traditional reservoir computer, thus simplifying training even further. Here, we study a particularly challenging problem of learning a dynamical system that has both disparate time scales and multiple co-existing dynamical states (attractors). We compare the next-generation and traditional reservoir computer using metrics quantifying the geometry of the ground-truth and forecasted attractors. For the studied four-dimensional system, the next-generation reservoir computing approach uses $\sim 1.7 \times$ less training data, requires $10^3 \times$ shorter `warm up' time, has fewer metaparameters, and has an $\sim 100\times$ higher accuracy in predicting the co-existing attractor characteristics in comparison to a traditional reservoir computer. Furthermore, we demonstrate that it predicts the basin of attraction with high accuracy. This work lends further support to the superior learning ability of this new machine learning algorithm for dynamical systems.

Inferring untrained complex dynamics of delay systems using an adapted echo state network

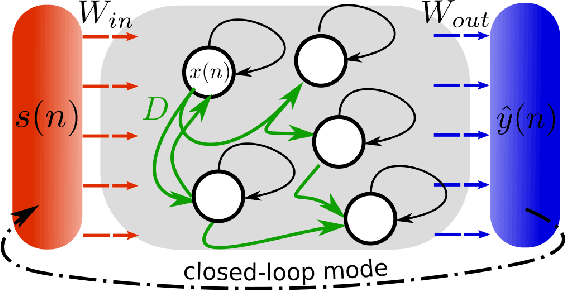
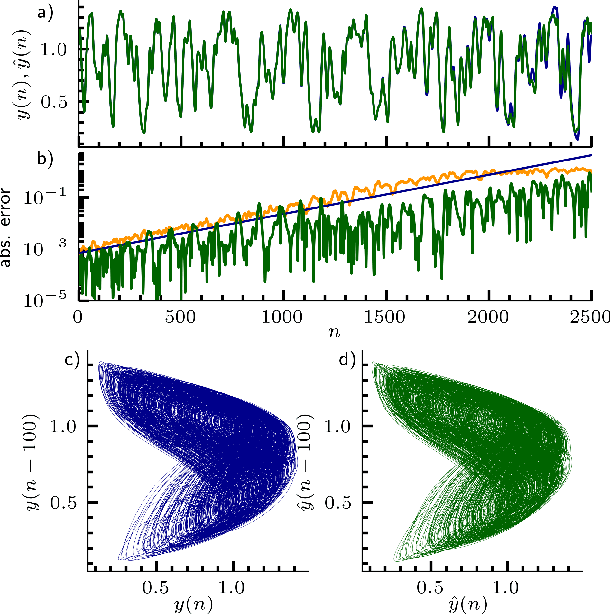
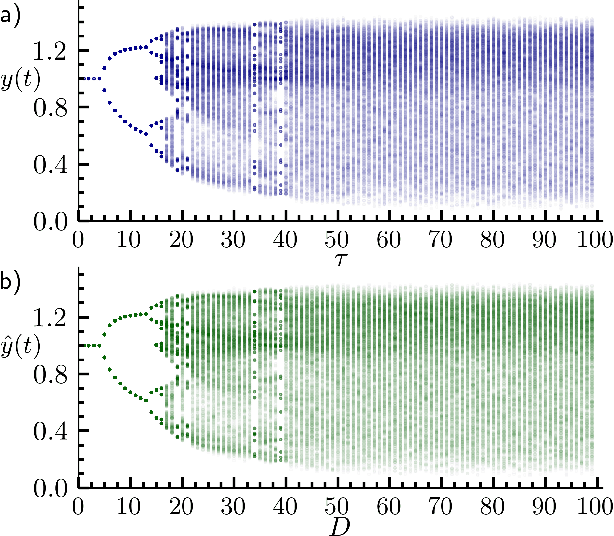
Caused by finite signal propagation velocities, many complex systems feature time delays that may induce high-dimensional chaotic behavior and make forecasting intricate. Here, we propose an echo state network adaptable to the physics of systems with arbitrary delays. After training the network to forecast a system with a unique and sufficiently long delay, it already learned to predict the system dynamics for all other delays. A simple adaptation of the network's topology allows us to infer untrained features such as high-dimensional chaotic attractors, bifurcations, and even multistabilities, that emerge with shorter and longer delays. Thus, the fusion of physical knowledge of the delay system and data-driven machine learning yields a model with high generalization capabilities and unprecedented prediction accuracy.

Model-free inference of unseen attractors: Reconstructing phase space features from a single noisy trajectory using reservoir computing

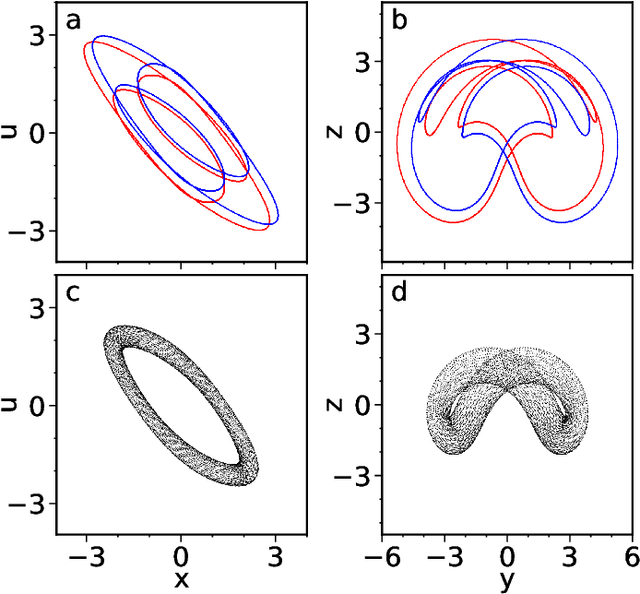
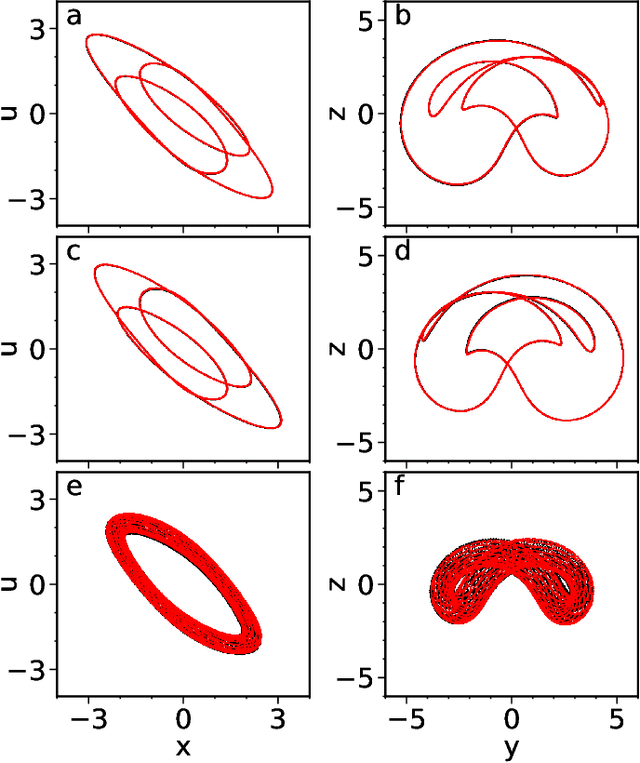
Reservoir computers are powerful tools for chaotic time series prediction. They can be trained to approximate phase space flows and can thus both predict future values to a high accuracy, as well as reconstruct the general properties of a chaotic attractor without requiring a model. In this work, we show that the ability to learn the dynamics of a complex system can be extended to systems with co-existing attractors, here a 4-dimensional extension of the well-known Lorenz chaotic system. We demonstrate that a reservoir computer can infer entirely unexplored parts of the phase space: a properly trained reservoir computer can predict the existence of attractors that were never approached during training and therefore are labelled as unseen. We provide examples where attractor inference is achieved after training solely on a single noisy trajectory.

56 GBaud PAM-4 100 km Transmission System with Photonic Processing Schemes

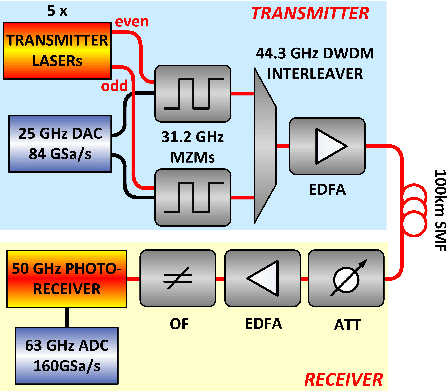
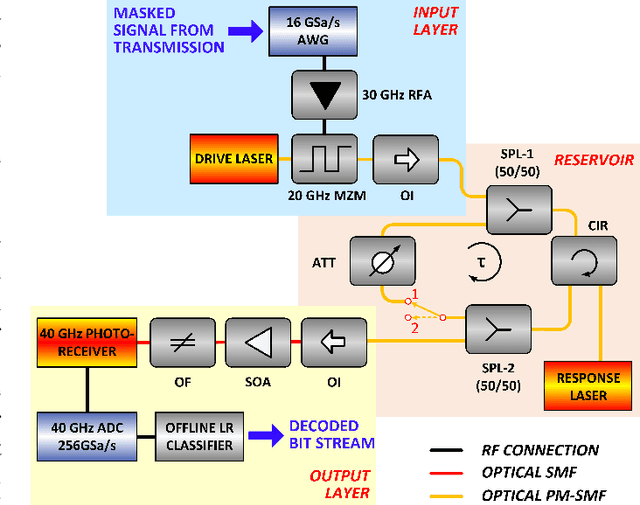
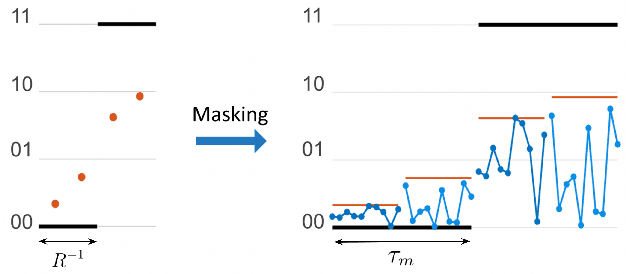
Analog photonic computing has been proposed and tested in recent years as an alternative approach for data recovery in fiber transmission systems. Photonic reservoir computing, performing nonlinear transformations of the transmitted signals and exhibiting internal fading memory, has been found advantageous for this kind of processing. In this work, we show that the effectiveness of the internal fading memory depends significantly on the properties of the signal to be processed. Specifically, we demonstrate two experimental photonic post-processing schemes for a 56 GBaud PAM-4 experimental transmission system, with 100 km uncompensated standard single-mode fiber and direct detection. We show that, for transmission systems with significant chromatic dispersion, the contribution of a photonic reservoir's fading memory to the computational performance is limited. In a comparison between the data recovery performances between a reservoir computing and an extreme learning machine fiber-based configuration, we find that both offer equivalent data recovery. The extreme learning machine approach eliminates the necessity of external recurrent connectivity, which simplifies the system and increases the computation speed. Error-free data recovery is experimentally demonstrated for an optical signal to noise ratio above 30 dB, outperforming an implementation of a Kramers-Kronig receiver in the digital domain.

Deep Learning with a Single Neuron: Folding a Deep Neural Network in Time using Feedback-Modulated Delay Loops

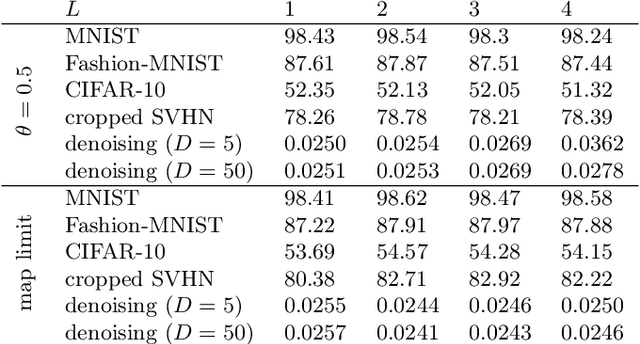
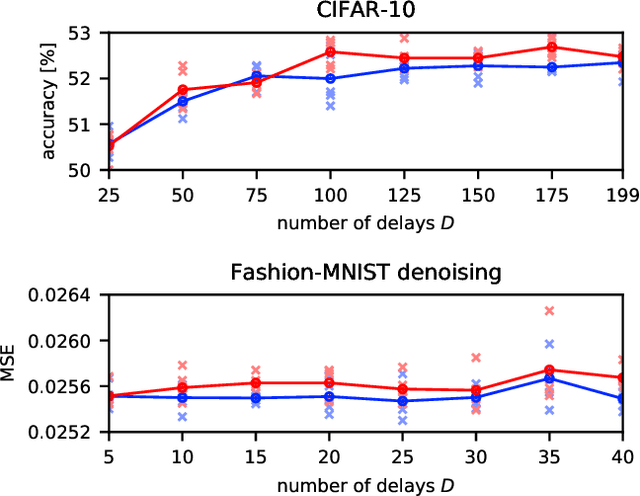
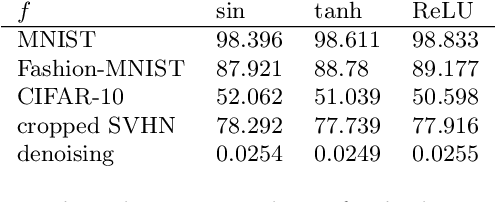
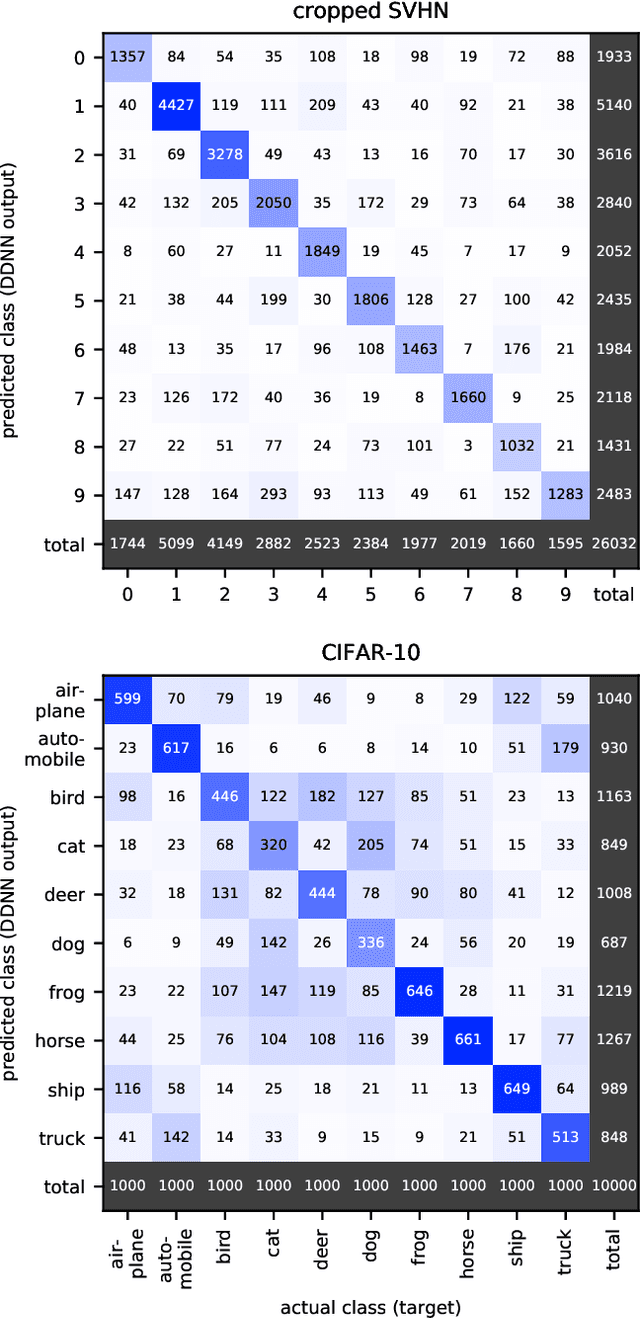
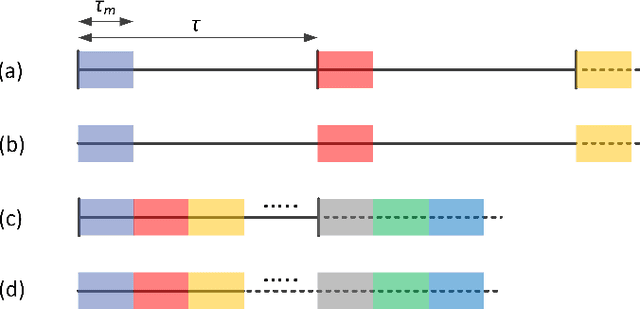
Deep neural networks are among the most widely applied machine learning tools showing outstanding performance in a broad range of tasks. We present a method for folding a deep neural network of arbitrary size into a single neuron with multiple time-delayed feedback loops. This single-neuron deep neural network comprises only a single nonlinearity and appropriately adjusted modulations of the feedback signals. The network states emerge in time as a temporal unfolding of the neuron's dynamics. By adjusting the feedback-modulation within the loops, we adapt the network's connection weights. These connection weights are determined via a modified back-propagation algorithm that we designed for such types of networks. Our approach fully recovers standard Deep Neural Networks (DNN), encompasses sparse DNNs, and extends the DNN concept toward dynamical systems implementations. The new method, which we call Folded-in-time DNN (Fit-DNN), exhibits promising performance in a set of benchmark tasks.

Reinforcement Learning in a large scale photonic Recurrent Neural Network

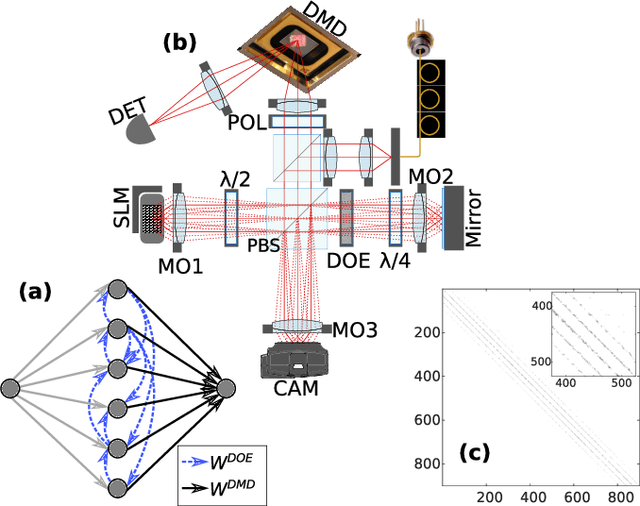
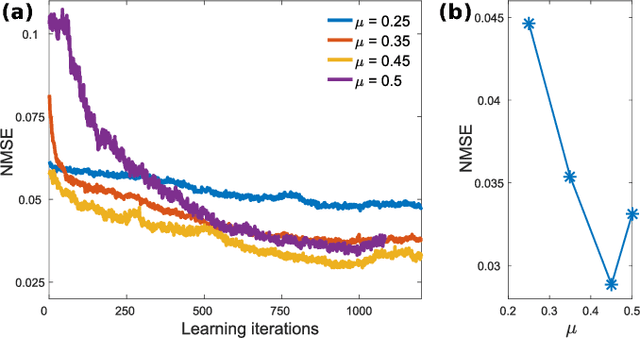
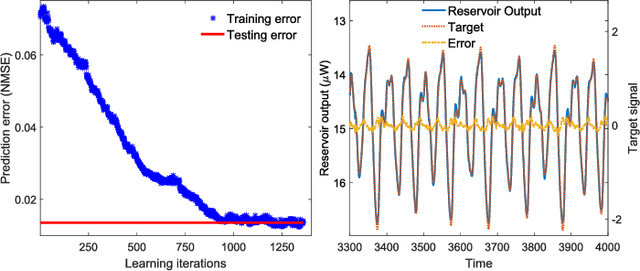
Photonic Neural Network implementations have been gaining considerable attention as a potentially disruptive future technology. Demonstrating learning in large scale neural networks is essential to establish photonic machine learning substrates as viable information processing systems. Realizing photonic Neural Networks with numerous nonlinear nodes in a fully parallel and efficient learning hardware was lacking so far. We demonstrate a network of up to 2500 diffractively coupled photonic nodes, forming a large scale Recurrent Neural Network. Using a Digital Micro Mirror Device, we realize reinforcement learning. Our scheme is fully parallel, and the passive weights maximize energy efficiency and bandwidth. The computational output efficiently converges and we achieve very good performance.

Photonic Delay Systems as Machine Learning Implementations

Nonlinear photonic delay systems present interesting implementation platforms for machine learning models. They can be extremely fast, offer great degrees of parallelism and potentially consume far less power than digital processors. So far they have been successfully employed for signal processing using the Reservoir Computing paradigm. In this paper we show that their range of applicability can be greatly extended if we use gradient descent with backpropagation through time on a model of the system to optimize the input encoding of such systems. We perform physical experiments that demonstrate that the obtained input encodings work well in reality, and we show that optimized systems perform significantly better than the common Reservoir Computing approach. The results presented here demonstrate that common gradient descent techniques from machine learning may well be applicable on physical neuro-inspired analog computers.