Fast Autofocusing using Tiny Transformer Networks for Digital Holographic Microscopy

The numerical wavefront backpropagation principle of digital holography confers unique extended focus capabilities, without mechanical displacements along z-axis. However, the determination of the correct focusing distance is a non-trivial and time consuming issue. A deep learning (DL) solution is proposed to cast the autofocusing as a regression problem and tested over both experimental and simulated holograms. Single wavelength digital holograms were recorded by a Digital Holographic Microscope (DHM) with a 10$\mathrm{x}$ microscope objective from a patterned target moving in 3D over an axial range of 92 $\mu$m. Tiny DL models are proposed and compared such as a tiny Vision Transformer (TViT), tiny VGG16 (TVGG) and a tiny Swin-Transfomer (TSwinT). The experiments show that the predicted focusing distance $Z_R^{\mathrm{Pred}}$ is accurately inferred with an accuracy of 1.2 $\mu$m in average in comparison with the DHM depth of field of 15 $\mu$m. Numerical simulations show that all tiny models give the $Z_R^{\mathrm{Pred}}$ with an error below 0.3 $\mu$m. Such a prospect would significantly improve the current capabilities of computer vision position sensing in applications such as 3D microscopy for life sciences or micro-robotics. Moreover, all models reach state of the art inference time on CPU, less than 25 ms per inference.

Boolean learning under noise-perturbations in hardware neural networks

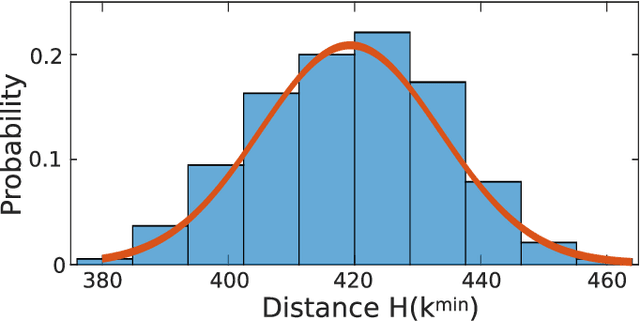
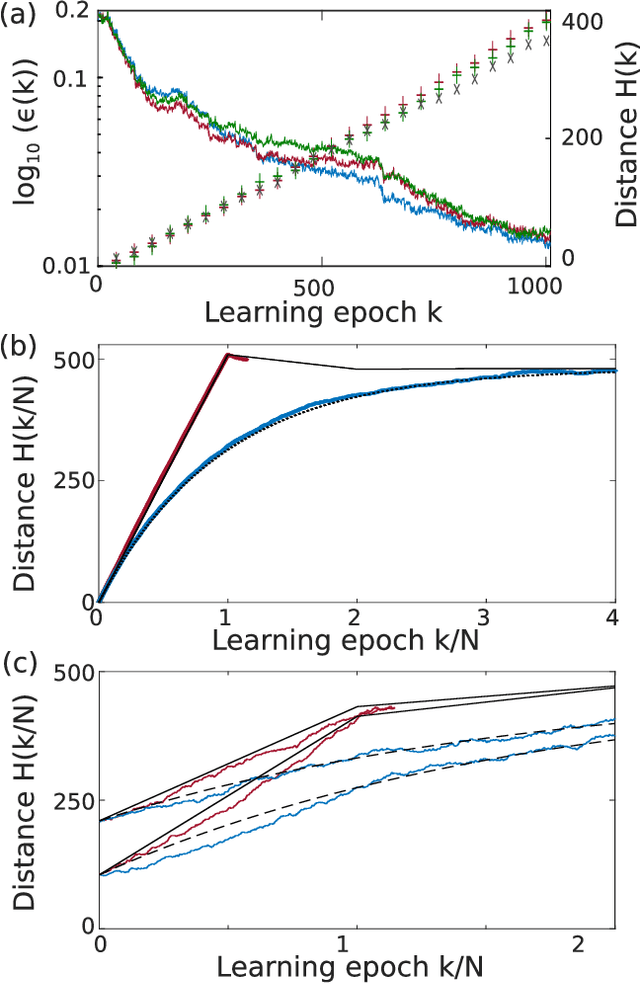
A high efficiency hardware integration of neural networks benefits from realizing nonlinearity, network connectivity and learning fully in a physical substrate. Multiple systems have recently implemented some or all of these operations, yet the focus was placed on addressing technological challenges. Fundamental questions regarding learning in hardware neural networks remain largely unexplored. Noise in particular is unavoidable in such architectures, and here we investigate its interaction with a learning algorithm using an opto-electronic recurrent neural network. We find that noise strongly modifies the system's path during convergence, and surprisingly fully decorrelates the final readout weight matrices. This highlights the importance of understanding architecture, noise and learning algorithm as interacting players, and therefore identifies the need for mathematical tools for noisy, analogue system optimization.

Three dimensional waveguide-interconnects for scalable integration of photonic neural networks

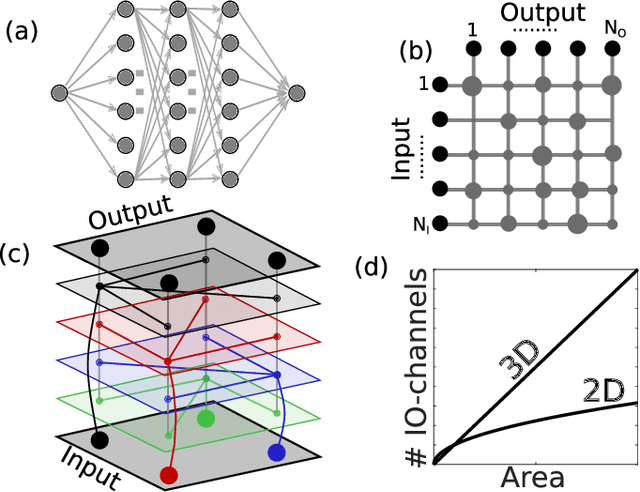
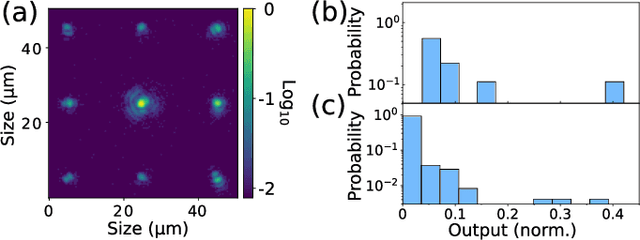
Photonic waveguides are prime candidates for integrated and parallel photonic interconnects. Such interconnects correspond to large-scale vector matrix products, which are at the heart of neural network computation. However, parallel interconnect circuits realized in two dimensions, for example by lithography, are strongly limited in size due to disadvantageous scaling. We use three dimensional (3D) printed photonic waveguides to overcome this limitation. 3D optical-couplers with fractal topology efficiently connect large numbers of input and output channels, and we show that the substrate's footprint area scales linearly. Going beyond simple couplers, we introduce functional circuits for discrete spatial filters identical to those used in deep convolutional neural networks.

Reservoir-size dependent learning in analogue neural networks

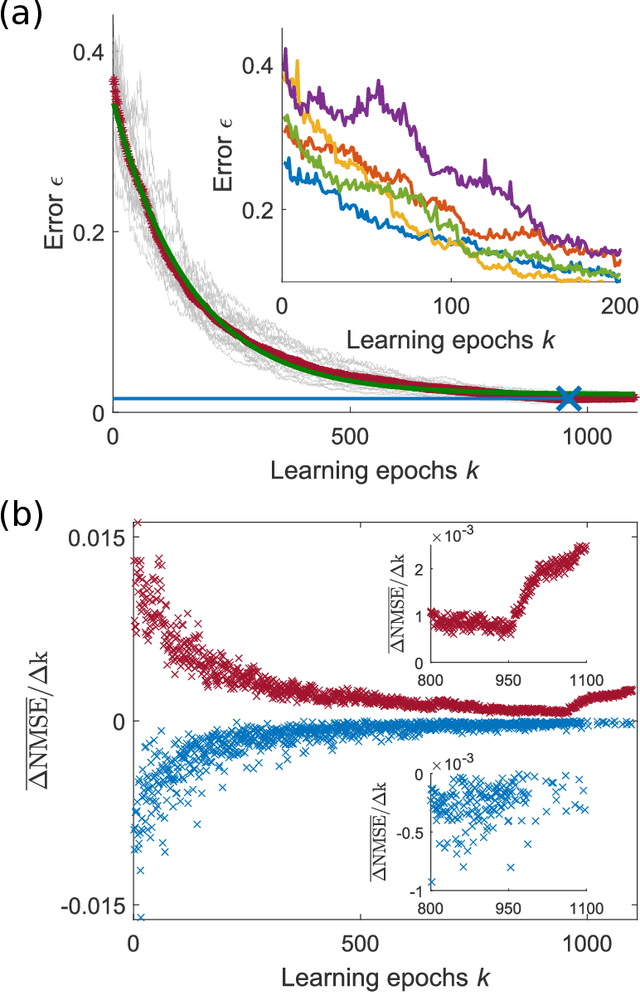
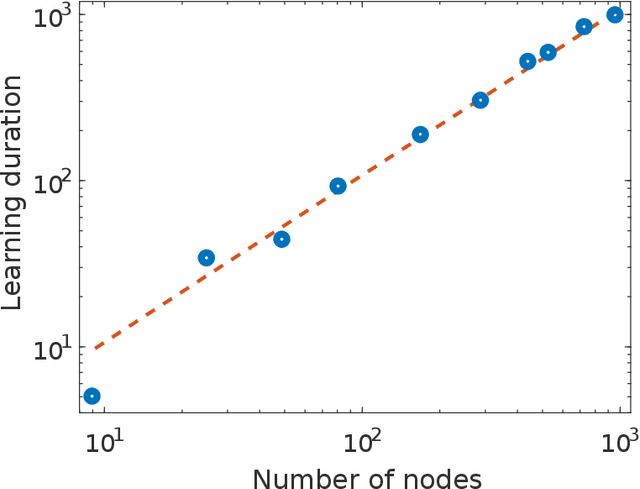
The implementation of artificial neural networks in hardware substrates is a major interdisciplinary enterprise. Well suited candidates for physical implementations must combine nonlinear neurons with dedicated and efficient hardware solutions for both connectivity and training. Reservoir computing addresses the problems related with the network connectivity and training in an elegant and efficient way. However, important questions regarding impact of reservoir size and learning routines on the convergence-speed during learning remain unaddressed. Here, we study in detail the learning process of a recently demonstrated photonic neural network based on a reservoir. We use a greedy algorithm to train our neural network for the task of chaotic signals prediction and analyze the learning-error landscape. Our results unveil fundamental properties of the system's optimization hyperspace. Particularly, we determine the convergence speed of learning as a function of reservoir size and find exceptional, close to linear scaling. This linear dependence, together with our parallel diffractive coupling, represent optimal scaling conditions for our photonic neural network scheme.

Fundamental aspects of noise in analog-hardware neural networks

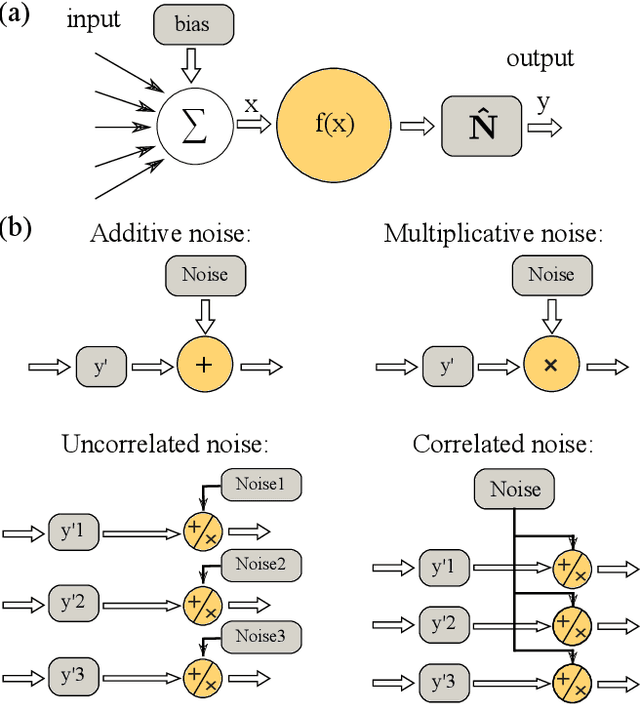
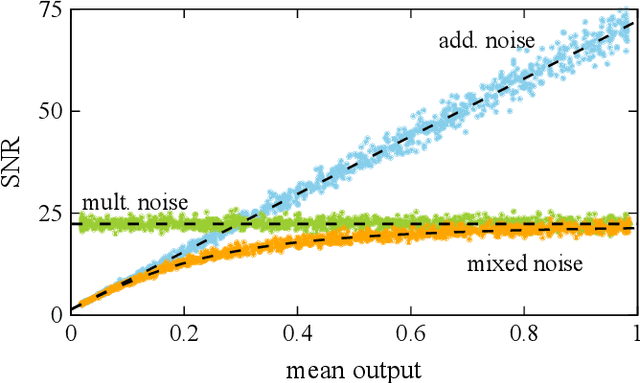
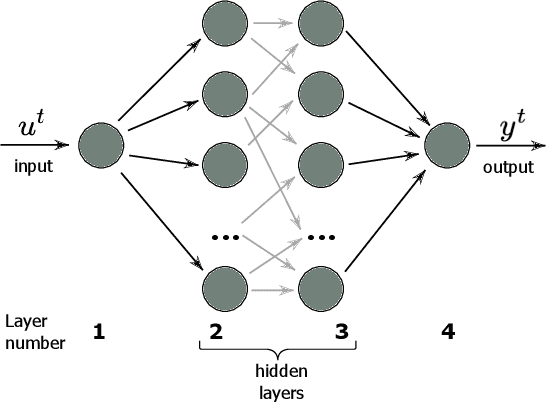
We study and analyze the fundamental aspects of noise propagation in recurrent as well as deep, multi-layer networks. The main focus of our study are neural networks in analogue hardware, yet the methodology provides insight for networks in general. The system under study consists of noisy linear nodes, and we investigate the signal-to-noise ratio at the network's outputs which is the upper limit to such a system's computing accuracy. We consider additive and multiplicative noise which can be purely local as well as correlated across populations of neurons. This covers the chief internal-perturbations of hardware networks and noise amplitudes were obtained from a physically implemented recurrent neural network and therefore correspond to a real-world system. Analytic solutions agree exceptionally well with numerical data, enabling clear identification of the most critical components and aspects for noise management. Focusing on linear nodes isolates the impact of network connections and allows us to derive strategies for mitigating noise. Our work is the starting point in addressing this aspect of analogue neural networks, and our results identify notoriously sensitive points while simultaneously highlighting the robustness of such computational systems.

Reinforcement Learning in a large scale photonic Recurrent Neural Network

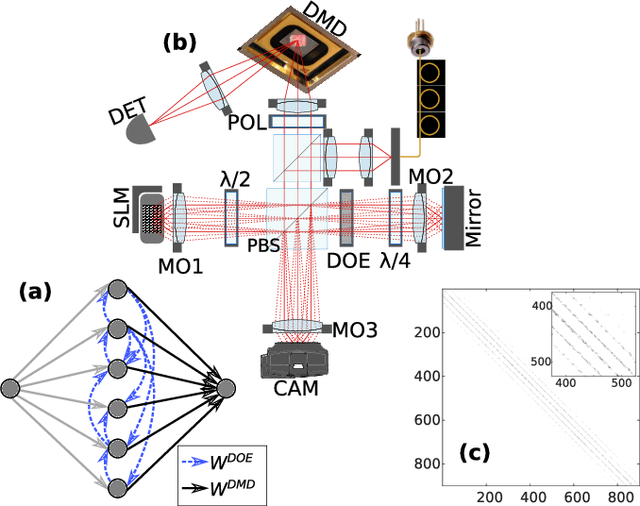
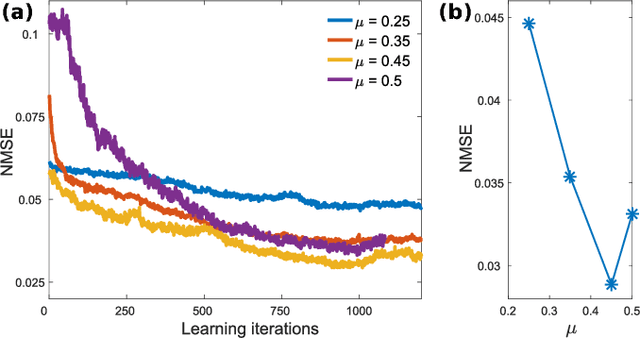
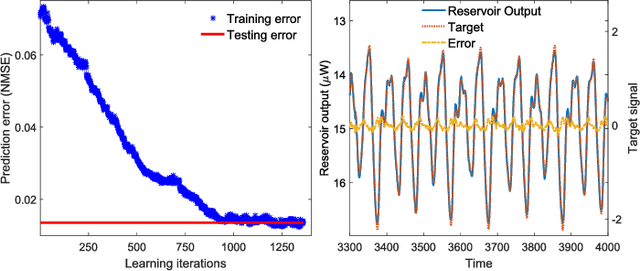
Photonic Neural Network implementations have been gaining considerable attention as a potentially disruptive future technology. Demonstrating learning in large scale neural networks is essential to establish photonic machine learning substrates as viable information processing systems. Realizing photonic Neural Networks with numerous nonlinear nodes in a fully parallel and efficient learning hardware was lacking so far. We demonstrate a network of up to 2500 diffractively coupled photonic nodes, forming a large scale Recurrent Neural Network. Using a Digital Micro Mirror Device, we realize reinforcement learning. Our scheme is fully parallel, and the passive weights maximize energy efficiency and bandwidth. The computational output efficiently converges and we achieve very good performance.