Xavier Porte
On-chip wave chaos for photonic extreme learning
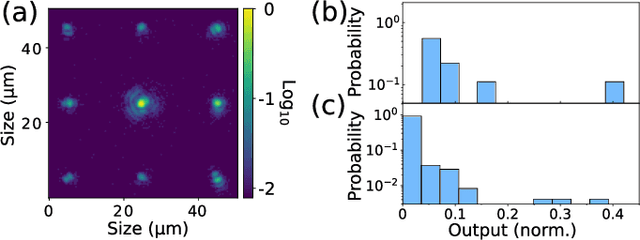
Aug 27, 2025Abstract:The increase in demand for scalable and energy efficient artificial neural networks has put the focus on novel hardware solutions. Integrated photonics offers a compact, parallel and ultra-fast information processing platform, specially suited for extreme learning machine (ELM) architectures. Here we experimentally demonstrate a chip-scale photonic ELM based on wave chaos interference in a stadium microcavity. By encoding the input information in the wavelength of an external single-frequency tunable laser source, we leverage the high sensitivity to wavelength of injection in such photonic resonators. We fabricate the microcavity with direct laser writing of SU-8 polymer on glass. A scattering wall surrounding the stadium operates as readout layer, collecting the light associated with the cavity's leaky modes. We report uncorrelated and aperiodic behavior in the speckles of the scattering barrier from a high resolution scan of the input wavelength. Finally, we characterize the system's performance at classification in four qualitatively different benchmark tasks. As we can control the number of output nodes of our ELM by measuring different parts of the scattering barrier, we demonstrate the capability to optimize our photonic ELM's readout size to the performance required for each task.
A spiking photonic neural network of 40.000 neurons, trained with rank-order coding for leveraging sparsity
Nov 28, 2024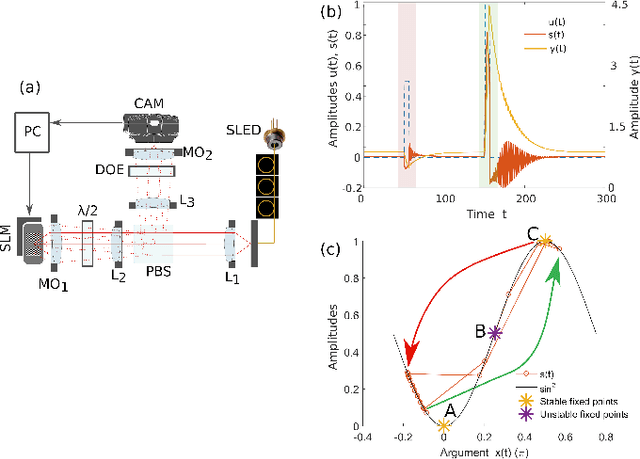
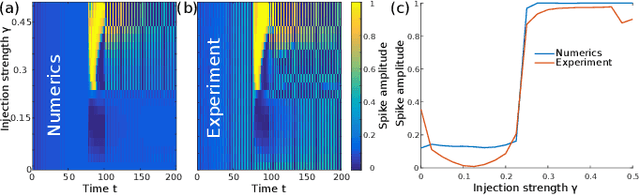
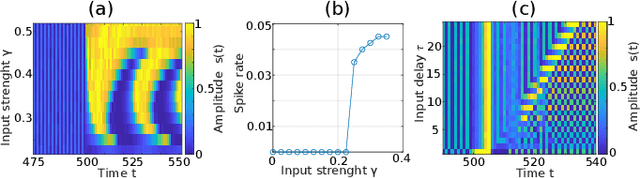
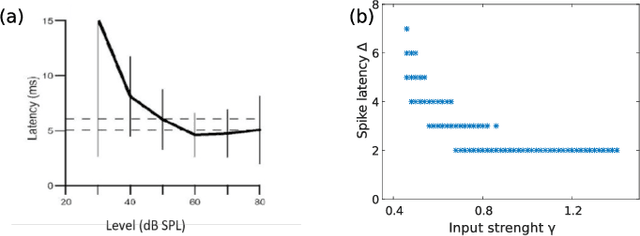
Abstract:In recent years, the hardware implementation of neural networks, leveraging physical coupling and analog neurons has substantially increased in relevance. Such nonlinear and complex physical networks provide significant advantages in speed and energy efficiency, but are potentially susceptible to internal noise when compared to digital emulations of such networks. In this work, we consider how additive and multiplicative Gaussian white noise on the neuronal level can affect the accuracy of the network when applied for specific tasks and including a softmax function in the readout layer. We adapt several noise reduction techniques to the essential setting of classification tasks, which represent a large fraction of neural network computing. We find that these adjusted concepts are highly effective in mitigating the detrimental impact of noise.
Convergence and scaling of Boolean-weight optimization for hardware reservoirs
May 13, 2023
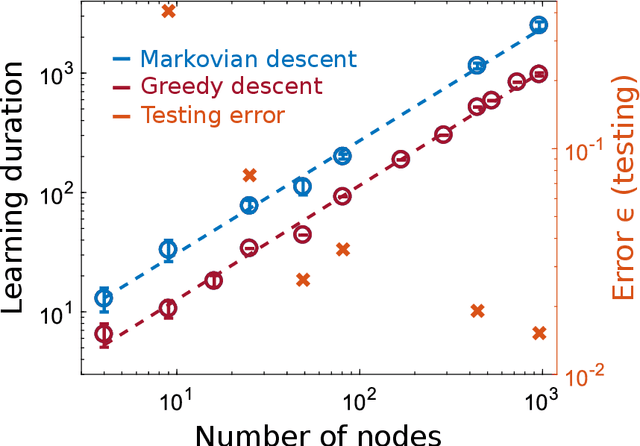
Abstract:Hardware implementation of neural network are an essential step to implement next generation efficient and powerful artificial intelligence solutions. Besides the realization of a parallel, efficient and scalable hardware architecture, the optimization of the system's extremely large parameter space with sampling-efficient approaches is essential. Here, we analytically derive the scaling laws for highly efficient Coordinate Descent applied to optimizing the readout layer of a random recurrently connection neural network, a reservoir. We demonstrate that the convergence is exponential and scales linear with the network's number of neurons. Our results perfectly reproduce the convergence and scaling of a large-scale photonic reservoir implemented in a proof-of-concept experiment. Our work therefore provides a solid foundation for such optimization in hardware networks, and identifies future directions that are promising for optimizing convergence speed during learning leveraging measures of a neural network's amplitude statistics and the weight update rule.
A complete, parallel and autonomous photonic neural network in a semiconductor multimode laser
Dec 21, 2020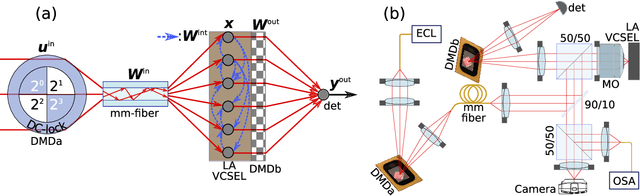
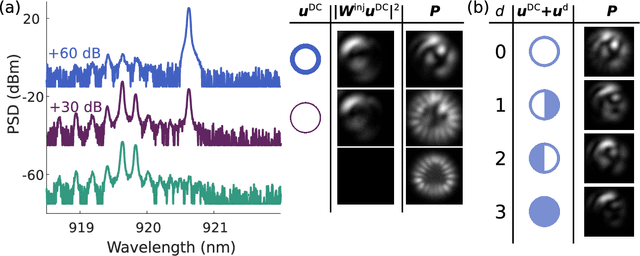
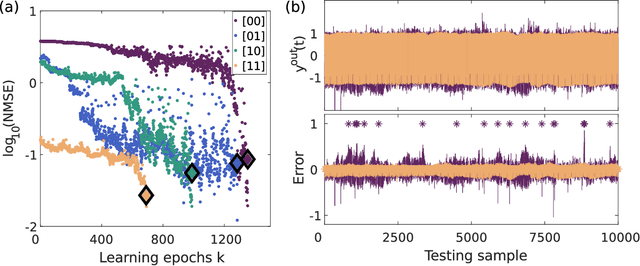
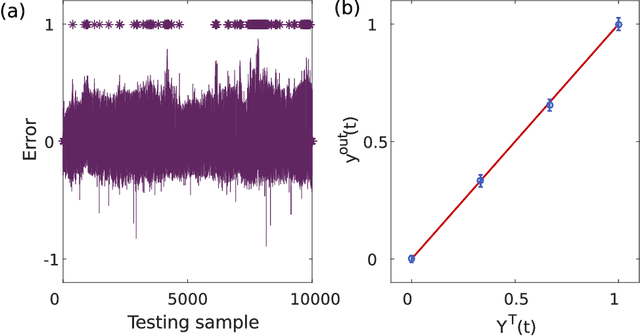
Abstract:Neural networks are one of the disruptive computing concepts of our time. However, they fundamentally differ from classical, algorithmic computing in a number of fundamental aspects. These differences result in equally fundamental, severe and relevant challenges for neural network computing using current computing substrates. Neural networks urge for parallelism across the entire processor and for a co-location of memory and arithmetic, i.e. beyond von Neumann architectures. Parallelism in particular made photonics a highly promising platform, yet until now scalable and integratable concepts are scarce. Here, we demonstrate for the first time how a fully parallel and fully implemented photonic neural network can be realized using spatially distributed modes of an efficient and fast semiconductor laser. Importantly, all neural network connections are realized in hardware, and our processor produces results without pre- or post-processing. 130+ nodes are implemented in a large-area vertical cavity surface emitting laser, input and output weights are realized via the complex transmission matrix of a multimode fiber and a digital micro-mirror array, respectively. We train the readout weights to perform 2-bit header recognition, a 2-bit XOR and 2-bit digital analog conversion, and obtain < 0.9 10^-3 and 2.9 10^-2 error rates for digit recognition and XOR, respectively. Finally, the digital analog conversion can be realized with a standard deviation of only 5.4 10^-2. Our system is scalable to much larger sizes and to bandwidths in excess of 20 GHz.
Boolean learning under noise-perturbations in hardware neural networks
Mar 27, 2020

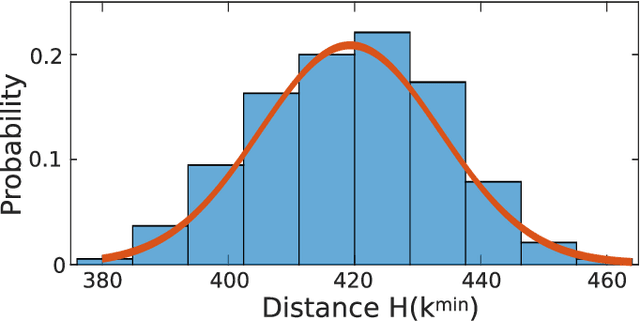
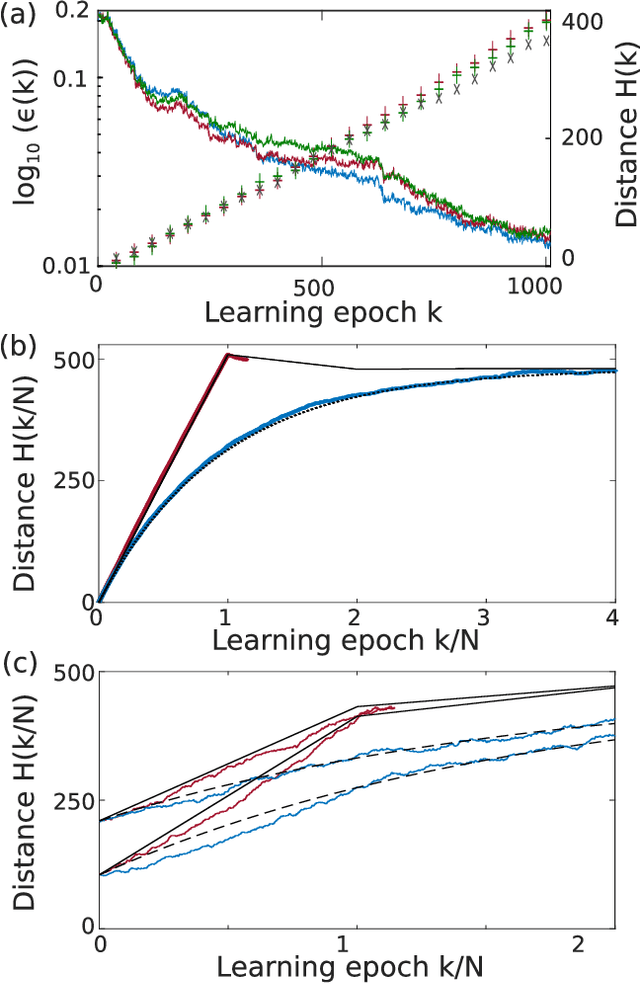
Abstract:A high efficiency hardware integration of neural networks benefits from realizing nonlinearity, network connectivity and learning fully in a physical substrate. Multiple systems have recently implemented some or all of these operations, yet the focus was placed on addressing technological challenges. Fundamental questions regarding learning in hardware neural networks remain largely unexplored. Noise in particular is unavoidable in such architectures, and here we investigate its interaction with a learning algorithm using an opto-electronic recurrent neural network. We find that noise strongly modifies the system's path during convergence, and surprisingly fully decorrelates the final readout weight matrices. This highlights the importance of understanding architecture, noise and learning algorithm as interacting players, and therefore identifies the need for mathematical tools for noisy, analogue system optimization.
Three dimensional waveguide-interconnects for scalable integration of photonic neural networks
Jan 09, 2020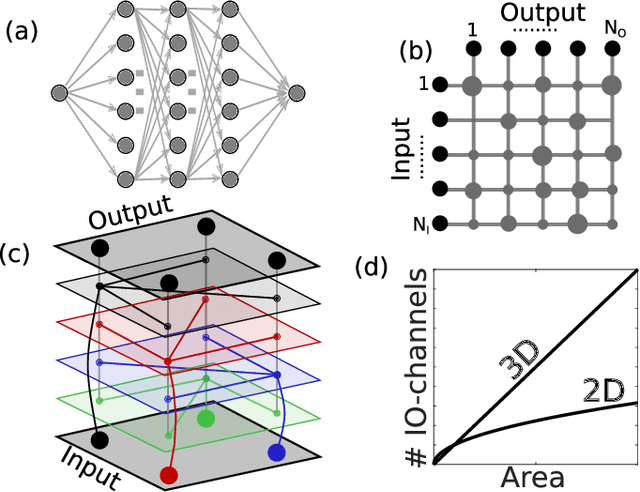


Abstract:Photonic waveguides are prime candidates for integrated and parallel photonic interconnects. Such interconnects correspond to large-scale vector matrix products, which are at the heart of neural network computation. However, parallel interconnect circuits realized in two dimensions, for example by lithography, are strongly limited in size due to disadvantageous scaling. We use three dimensional (3D) printed photonic waveguides to overcome this limitation. 3D optical-couplers with fractal topology efficiently connect large numbers of input and output channels, and we show that the substrate's footprint area scales linearly. Going beyond simple couplers, we introduce functional circuits for discrete spatial filters identical to those used in deep convolutional neural networks.
Reservoir-size dependent learning in analogue neural networks
Jul 23, 2019
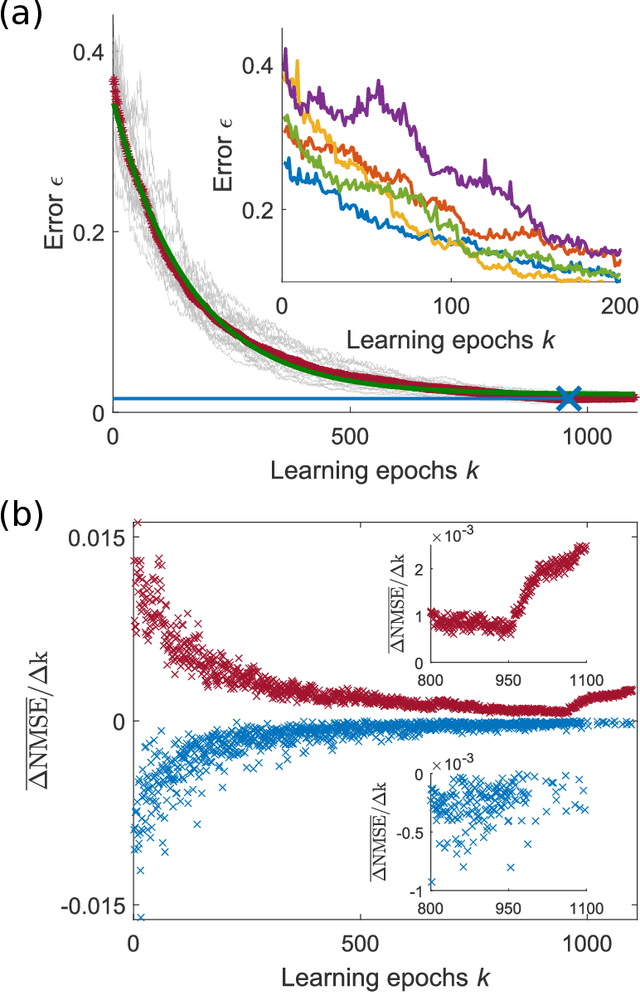
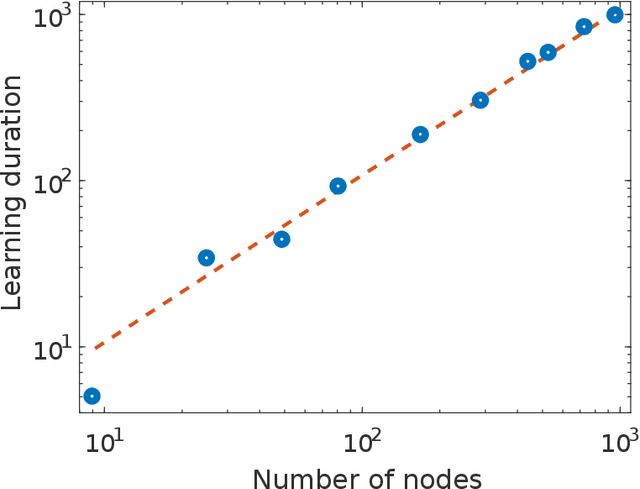
Abstract:The implementation of artificial neural networks in hardware substrates is a major interdisciplinary enterprise. Well suited candidates for physical implementations must combine nonlinear neurons with dedicated and efficient hardware solutions for both connectivity and training. Reservoir computing addresses the problems related with the network connectivity and training in an elegant and efficient way. However, important questions regarding impact of reservoir size and learning routines on the convergence-speed during learning remain unaddressed. Here, we study in detail the learning process of a recently demonstrated photonic neural network based on a reservoir. We use a greedy algorithm to train our neural network for the task of chaotic signals prediction and analyze the learning-error landscape. Our results unveil fundamental properties of the system's optimization hyperspace. Particularly, we determine the convergence speed of learning as a function of reservoir size and find exceptional, close to linear scaling. This linear dependence, together with our parallel diffractive coupling, represent optimal scaling conditions for our photonic neural network scheme.
Fundamental aspects of noise in analog-hardware neural networks
Jul 21, 2019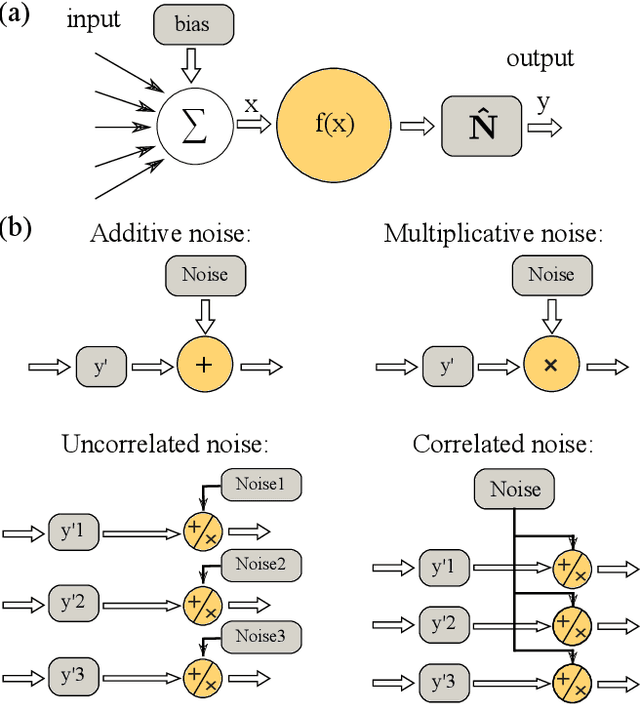
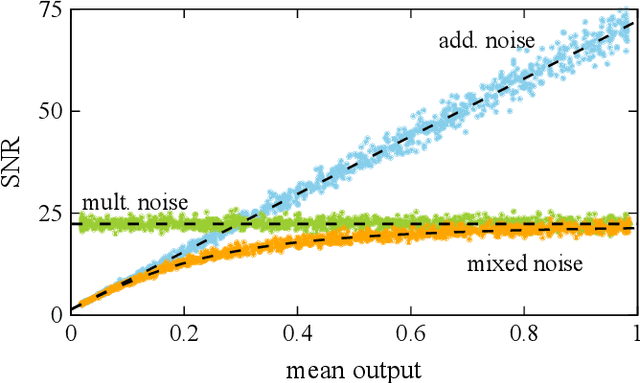
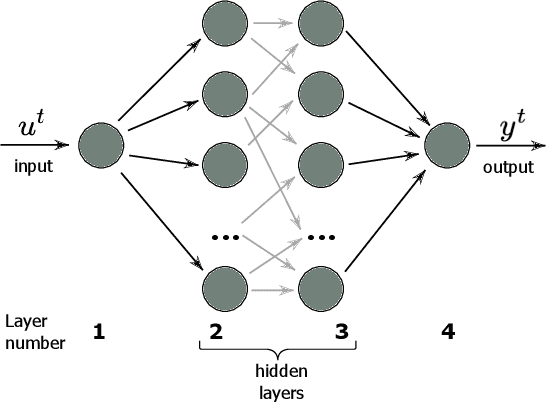

Abstract:We study and analyze the fundamental aspects of noise propagation in recurrent as well as deep, multi-layer networks. The main focus of our study are neural networks in analogue hardware, yet the methodology provides insight for networks in general. The system under study consists of noisy linear nodes, and we investigate the signal-to-noise ratio at the network's outputs which is the upper limit to such a system's computing accuracy. We consider additive and multiplicative noise which can be purely local as well as correlated across populations of neurons. This covers the chief internal-perturbations of hardware networks and noise amplitudes were obtained from a physically implemented recurrent neural network and therefore correspond to a real-world system. Analytic solutions agree exceptionally well with numerical data, enabling clear identification of the most critical components and aspects for noise management. Focusing on linear nodes isolates the impact of network connections and allows us to derive strategies for mitigating noise. Our work is the starting point in addressing this aspect of analogue neural networks, and our results identify notoriously sensitive points while simultaneously highlighting the robustness of such computational systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge