Convergence and scaling of Boolean-weight optimization for hardware reservoirs
Paper and Code
May 13, 2023
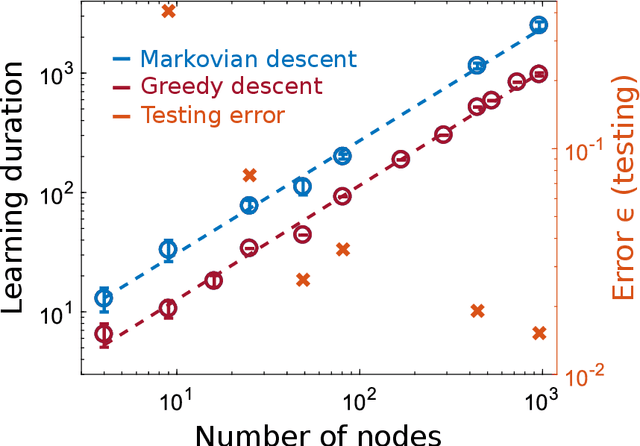
Hardware implementation of neural network are an essential step to implement next generation efficient and powerful artificial intelligence solutions. Besides the realization of a parallel, efficient and scalable hardware architecture, the optimization of the system's extremely large parameter space with sampling-efficient approaches is essential. Here, we analytically derive the scaling laws for highly efficient Coordinate Descent applied to optimizing the readout layer of a random recurrently connection neural network, a reservoir. We demonstrate that the convergence is exponential and scales linear with the network's number of neurons. Our results perfectly reproduce the convergence and scaling of a large-scale photonic reservoir implemented in a proof-of-concept experiment. Our work therefore provides a solid foundation for such optimization in hardware networks, and identifies future directions that are promising for optimizing convergence speed during learning leveraging measures of a neural network's amplitude statistics and the weight update rule.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge