Convergence and scaling of Boolean-weight optimization for hardware reservoirs

Hardware implementation of neural network are an essential step to implement next generation efficient and powerful artificial intelligence solutions. Besides the realization of a parallel, efficient and scalable hardware architecture, the optimization of the system's extremely large parameter space with sampling-efficient approaches is essential. Here, we analytically derive the scaling laws for highly efficient Coordinate Descent applied to optimizing the readout layer of a random recurrently connection neural network, a reservoir. We demonstrate that the convergence is exponential and scales linear with the network's number of neurons. Our results perfectly reproduce the convergence and scaling of a large-scale photonic reservoir implemented in a proof-of-concept experiment. Our work therefore provides a solid foundation for such optimization in hardware networks, and identifies future directions that are promising for optimizing convergence speed during learning leveraging measures of a neural network's amplitude statistics and the weight update rule.

Boolean learning under noise-perturbations in hardware neural networks

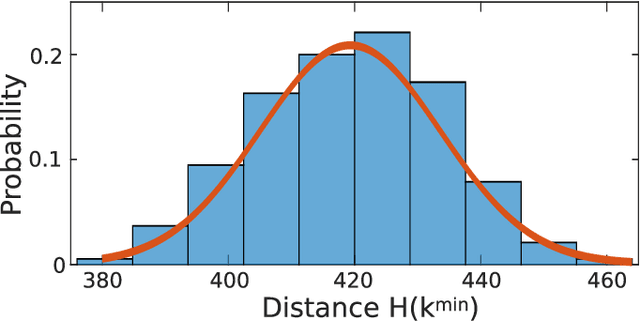
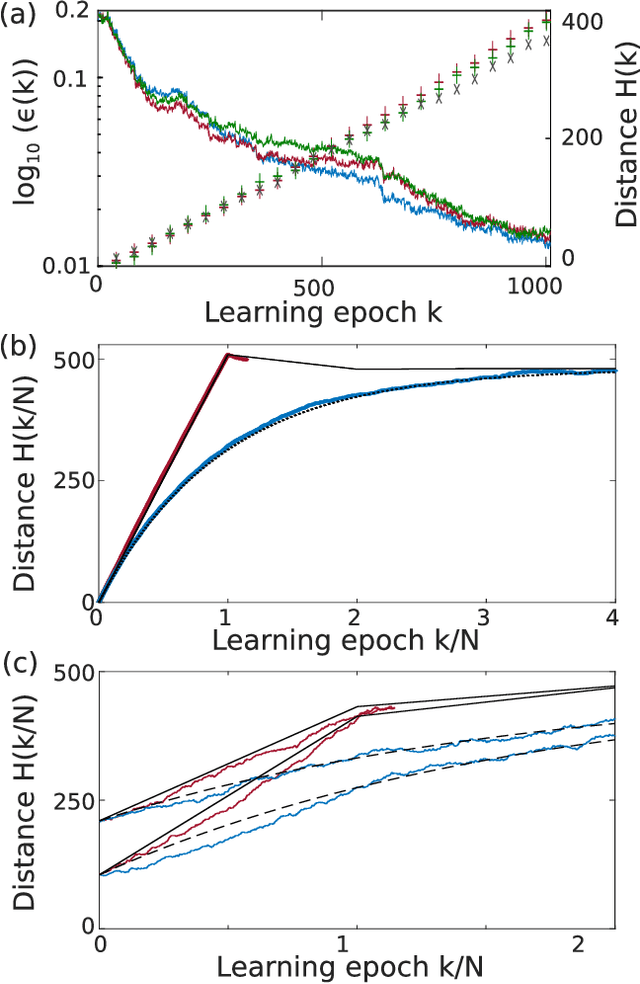
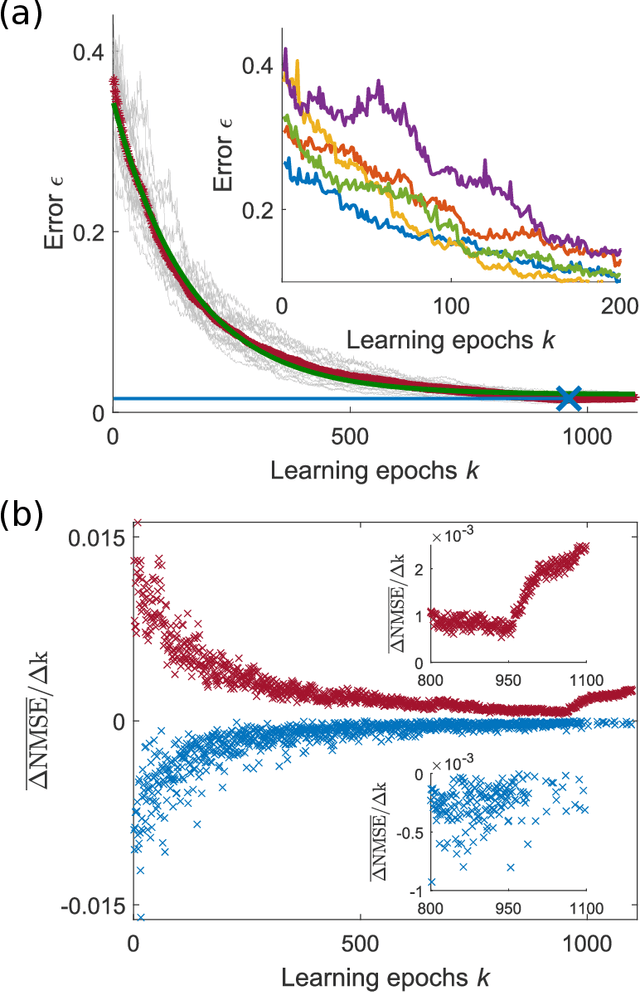
A high efficiency hardware integration of neural networks benefits from realizing nonlinearity, network connectivity and learning fully in a physical substrate. Multiple systems have recently implemented some or all of these operations, yet the focus was placed on addressing technological challenges. Fundamental questions regarding learning in hardware neural networks remain largely unexplored. Noise in particular is unavoidable in such architectures, and here we investigate its interaction with a learning algorithm using an opto-electronic recurrent neural network. We find that noise strongly modifies the system's path during convergence, and surprisingly fully decorrelates the final readout weight matrices. This highlights the importance of understanding architecture, noise and learning algorithm as interacting players, and therefore identifies the need for mathematical tools for noisy, analogue system optimization.

Reservoir-size dependent learning in analogue neural networks

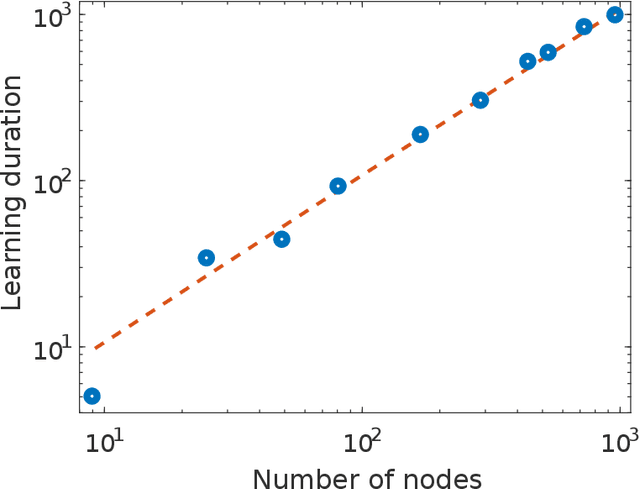
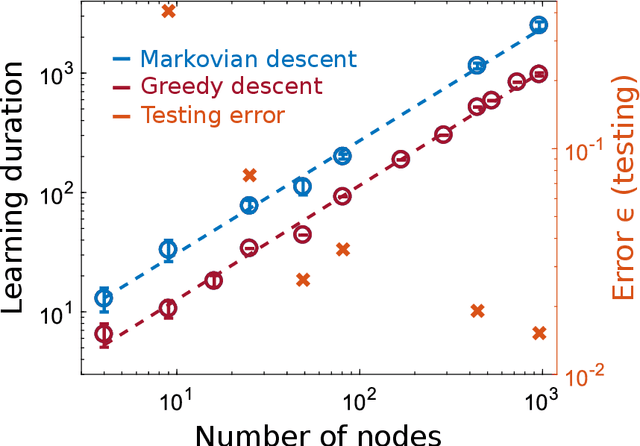
The implementation of artificial neural networks in hardware substrates is a major interdisciplinary enterprise. Well suited candidates for physical implementations must combine nonlinear neurons with dedicated and efficient hardware solutions for both connectivity and training. Reservoir computing addresses the problems related with the network connectivity and training in an elegant and efficient way. However, important questions regarding impact of reservoir size and learning routines on the convergence-speed during learning remain unaddressed. Here, we study in detail the learning process of a recently demonstrated photonic neural network based on a reservoir. We use a greedy algorithm to train our neural network for the task of chaotic signals prediction and analyze the learning-error landscape. Our results unveil fundamental properties of the system's optimization hyperspace. Particularly, we determine the convergence speed of learning as a function of reservoir size and find exceptional, close to linear scaling. This linear dependence, together with our parallel diffractive coupling, represent optimal scaling conditions for our photonic neural network scheme.

Fundamental aspects of noise in analog-hardware neural networks

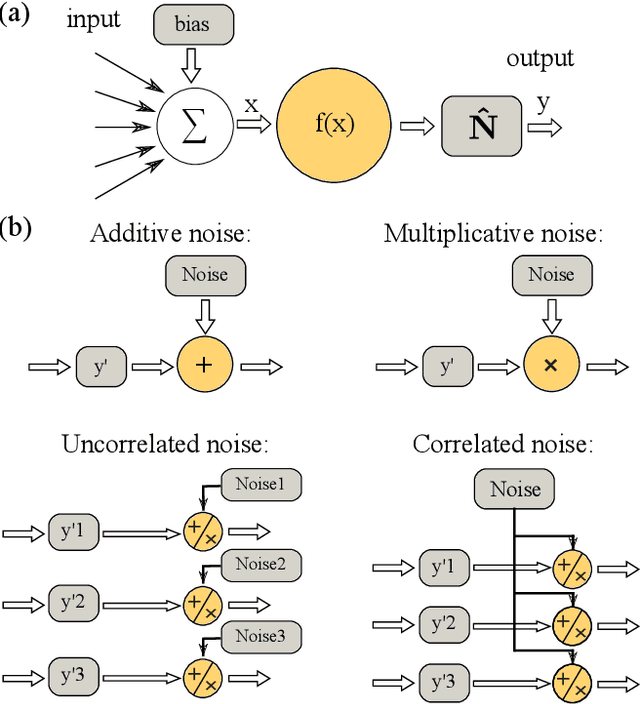
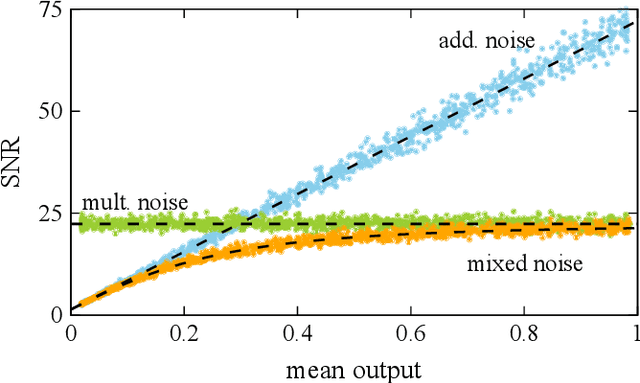
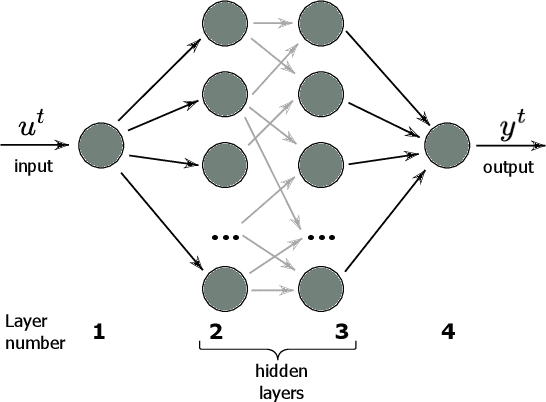
We study and analyze the fundamental aspects of noise propagation in recurrent as well as deep, multi-layer networks. The main focus of our study are neural networks in analogue hardware, yet the methodology provides insight for networks in general. The system under study consists of noisy linear nodes, and we investigate the signal-to-noise ratio at the network's outputs which is the upper limit to such a system's computing accuracy. We consider additive and multiplicative noise which can be purely local as well as correlated across populations of neurons. This covers the chief internal-perturbations of hardware networks and noise amplitudes were obtained from a physically implemented recurrent neural network and therefore correspond to a real-world system. Analytic solutions agree exceptionally well with numerical data, enabling clear identification of the most critical components and aspects for noise management. Focusing on linear nodes isolates the impact of network connections and allows us to derive strategies for mitigating noise. Our work is the starting point in addressing this aspect of analogue neural networks, and our results identify notoriously sensitive points while simultaneously highlighting the robustness of such computational systems.