The general aspects of noise in analogue hardware deep neural networks

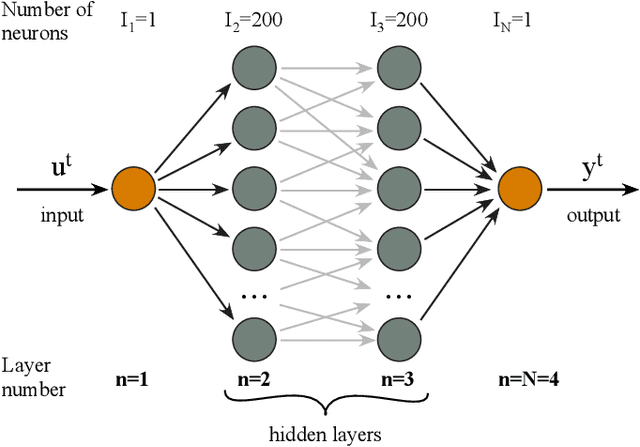
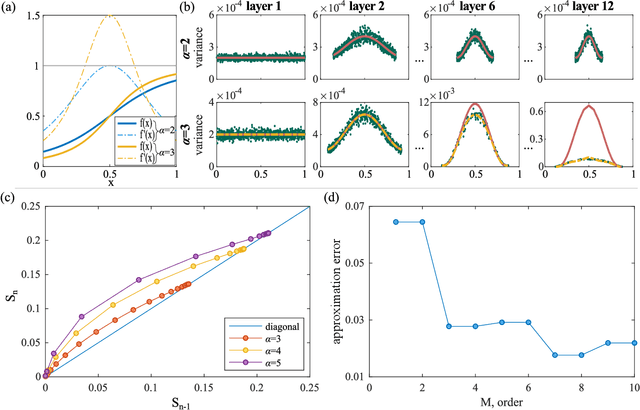
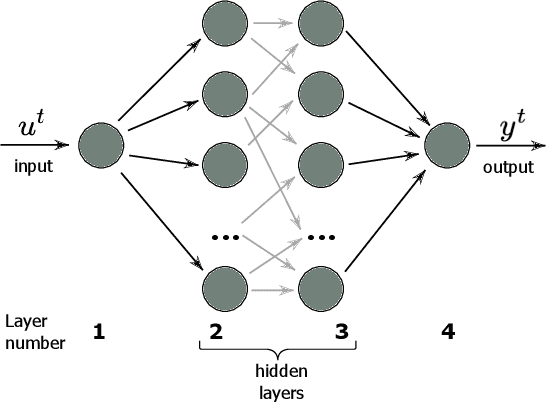
Deep neural networks unlocked a vast range of new applications by solving tasks of which many were previouslydeemed as reserved to higher human intelligence. One of the developments enabling this success was a boost incomputing power provided by special purpose hardware, such as graphic or tensor processing units. However,these do not leverage fundamental features of neural networks like parallelism and analog state variables.Instead, they emulate neural networks relying on computing power, which results in unsustainable energyconsumption and comparatively low speed. Fully parallel and analogue hardware promises to overcomethese challenges, yet the impact of analogue neuron noise and its propagation, i.e. accumulation, threatensrendering such approaches inept. Here, we analyse for the first time the propagation of noise in paralleldeep neural networks comprising noisy nonlinear neurons. We develop an analytical treatment for both,symmetric networks to highlight the underlying mechanisms, and networks trained with back propagation.We find that noise accumulation is generally bound, and adding additional network layers does not worsenthe signal to noise ratio beyond this limit. Most importantly, noise accumulation can be suppressed entirelywhen neuron activation functions have a slope smaller than unity. We therefore developed the frameworkfor noise of deep neural networks implemented in analog systems, and identify criteria allowing engineers todesign noise-resilient novel neural network hardware.

Boolean learning under noise-perturbations in hardware neural networks

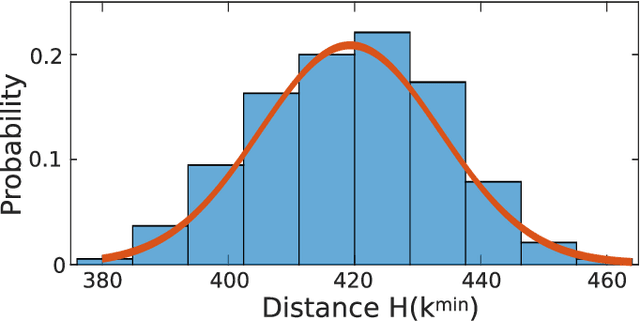
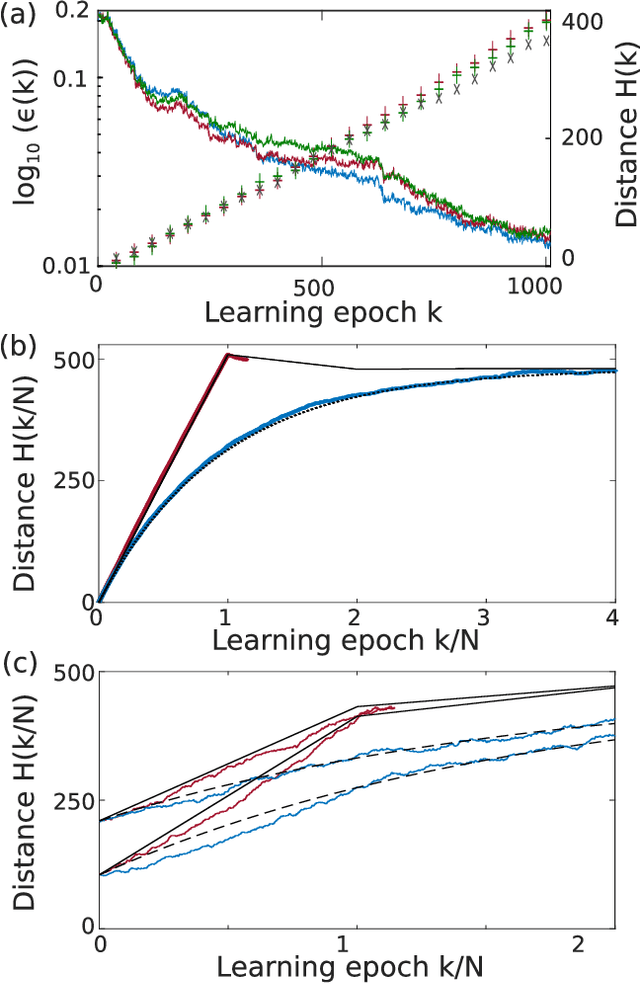
A high efficiency hardware integration of neural networks benefits from realizing nonlinearity, network connectivity and learning fully in a physical substrate. Multiple systems have recently implemented some or all of these operations, yet the focus was placed on addressing technological challenges. Fundamental questions regarding learning in hardware neural networks remain largely unexplored. Noise in particular is unavoidable in such architectures, and here we investigate its interaction with a learning algorithm using an opto-electronic recurrent neural network. We find that noise strongly modifies the system's path during convergence, and surprisingly fully decorrelates the final readout weight matrices. This highlights the importance of understanding architecture, noise and learning algorithm as interacting players, and therefore identifies the need for mathematical tools for noisy, analogue system optimization.

Three dimensional waveguide-interconnects for scalable integration of photonic neural networks

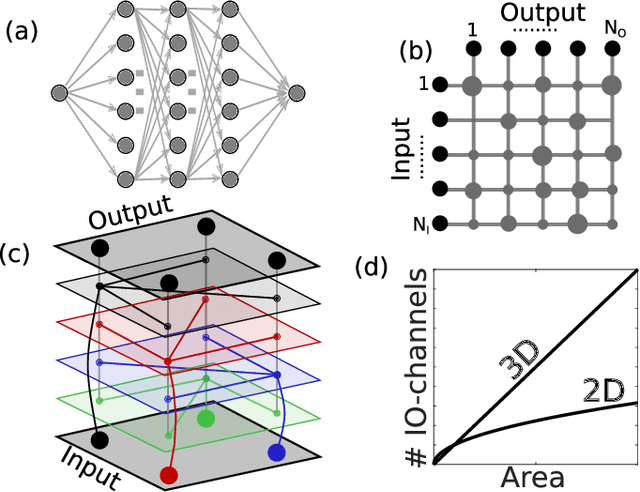
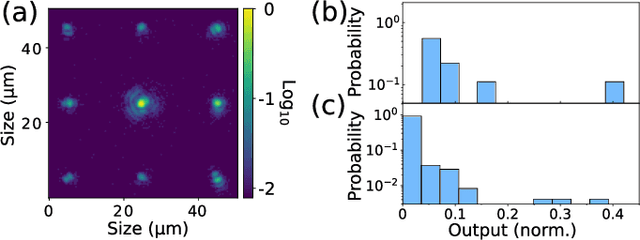
Photonic waveguides are prime candidates for integrated and parallel photonic interconnects. Such interconnects correspond to large-scale vector matrix products, which are at the heart of neural network computation. However, parallel interconnect circuits realized in two dimensions, for example by lithography, are strongly limited in size due to disadvantageous scaling. We use three dimensional (3D) printed photonic waveguides to overcome this limitation. 3D optical-couplers with fractal topology efficiently connect large numbers of input and output channels, and we show that the substrate's footprint area scales linearly. Going beyond simple couplers, we introduce functional circuits for discrete spatial filters identical to those used in deep convolutional neural networks.

Reservoir-size dependent learning in analogue neural networks

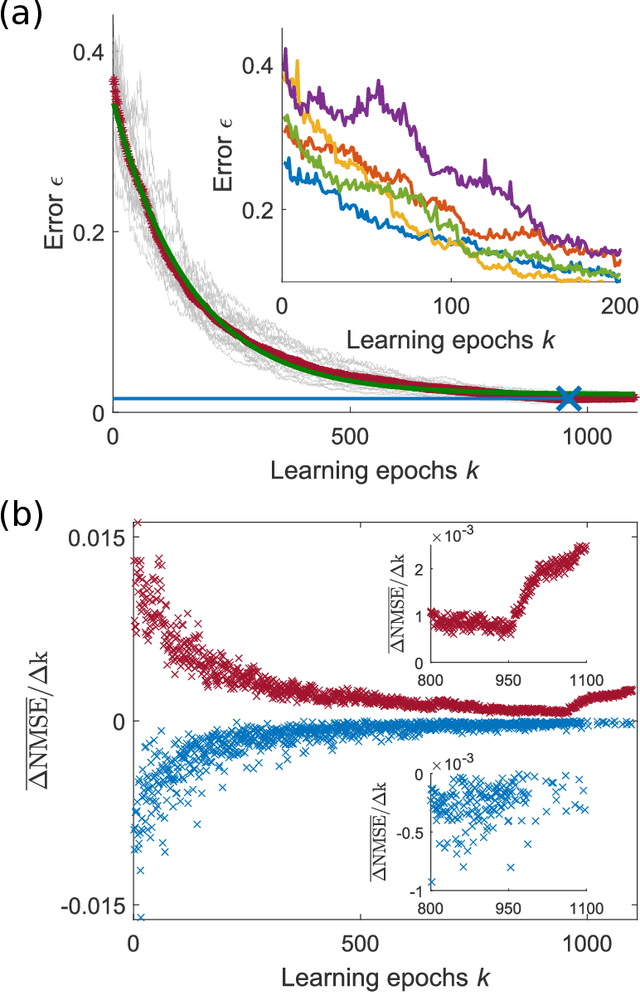
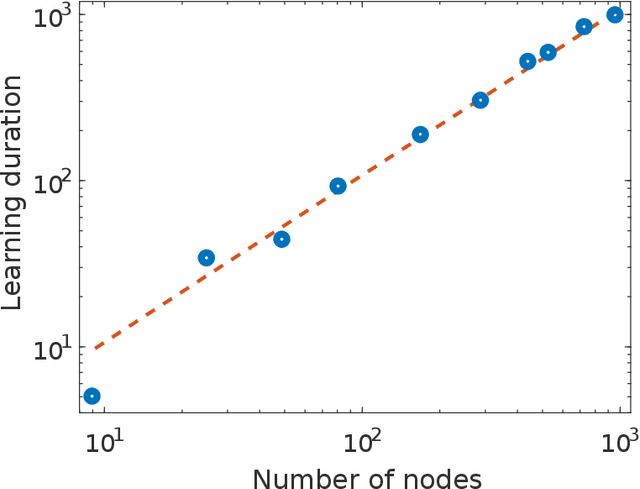
The implementation of artificial neural networks in hardware substrates is a major interdisciplinary enterprise. Well suited candidates for physical implementations must combine nonlinear neurons with dedicated and efficient hardware solutions for both connectivity and training. Reservoir computing addresses the problems related with the network connectivity and training in an elegant and efficient way. However, important questions regarding impact of reservoir size and learning routines on the convergence-speed during learning remain unaddressed. Here, we study in detail the learning process of a recently demonstrated photonic neural network based on a reservoir. We use a greedy algorithm to train our neural network for the task of chaotic signals prediction and analyze the learning-error landscape. Our results unveil fundamental properties of the system's optimization hyperspace. Particularly, we determine the convergence speed of learning as a function of reservoir size and find exceptional, close to linear scaling. This linear dependence, together with our parallel diffractive coupling, represent optimal scaling conditions for our photonic neural network scheme.

Fundamental aspects of noise in analog-hardware neural networks

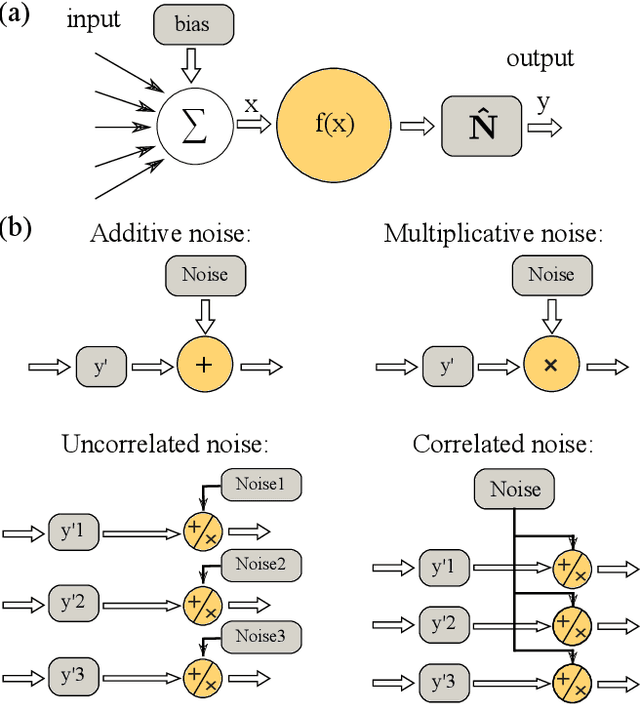
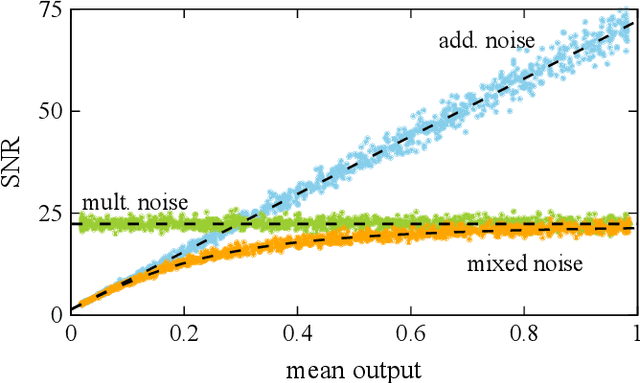
We study and analyze the fundamental aspects of noise propagation in recurrent as well as deep, multi-layer networks. The main focus of our study are neural networks in analogue hardware, yet the methodology provides insight for networks in general. The system under study consists of noisy linear nodes, and we investigate the signal-to-noise ratio at the network's outputs which is the upper limit to such a system's computing accuracy. We consider additive and multiplicative noise which can be purely local as well as correlated across populations of neurons. This covers the chief internal-perturbations of hardware networks and noise amplitudes were obtained from a physically implemented recurrent neural network and therefore correspond to a real-world system. Analytic solutions agree exceptionally well with numerical data, enabling clear identification of the most critical components and aspects for noise management. Focusing on linear nodes isolates the impact of network connections and allows us to derive strategies for mitigating noise. Our work is the starting point in addressing this aspect of analogue neural networks, and our results identify notoriously sensitive points while simultaneously highlighting the robustness of such computational systems.

Efficient Design of Hardware-Enabled Reservoir Computing in FPGAs

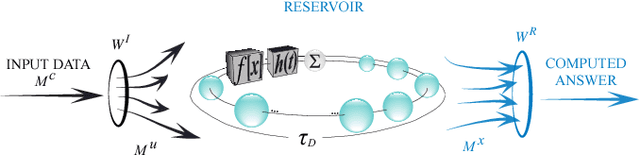
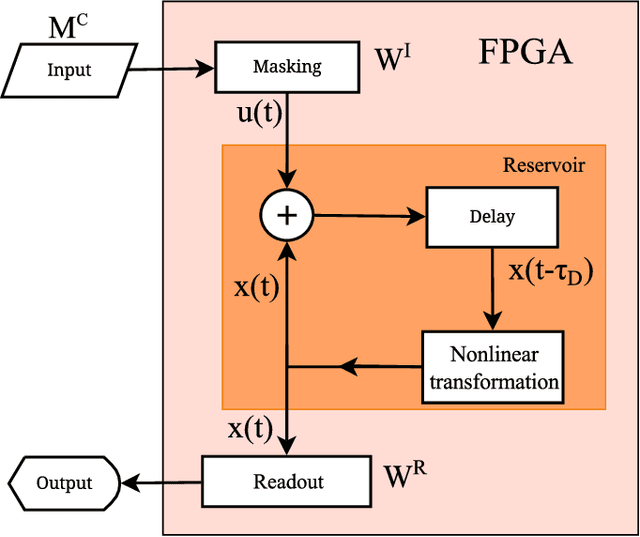
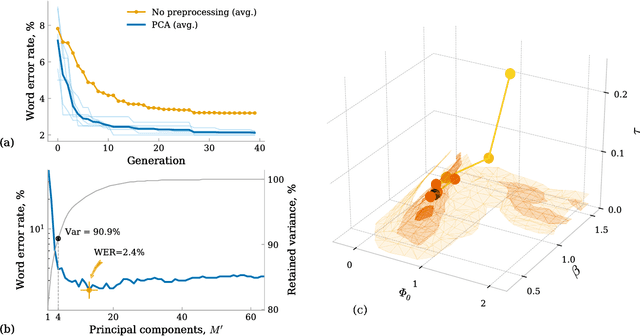
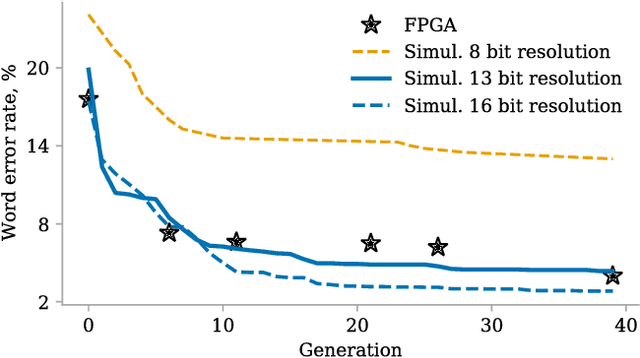
In this work, we propose a new approach towards the efficient optimization and implementation of reservoir computing hardware reducing the required domain expert knowledge and optimization effort. First, we adapt the reservoir input mask to the structure of the data via linear autoencoders. We therefore incorporate the advantages of dimensionality reduction and dimensionality expansion achieved by conventional algorithmically efficient linear algebra procedures of principal component analysis. Second, we employ evolutionary-inspired genetic algorithm techniques resulting in a highly efficient optimization of reservoir dynamics with dramatically reduced number of evaluations comparing to exhaustive search. We illustrate the method on the so-called single-node reservoir computing architecture, especially suitable for implementation in ultrahigh-speed hardware. The combination of both methods and the resulting reduction of time required for performance optimization of a hardware system establish a strategy towards machine learning hardware capable of self-adaption to optimally solve specific problems. We confirm the validity of those principles building reservoir computing hardware based on a field-programmable gate array.

Reinforcement Learning in a large scale photonic Recurrent Neural Network

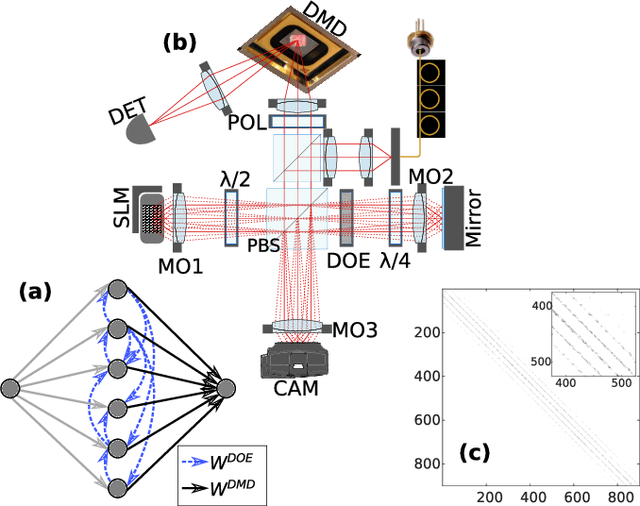
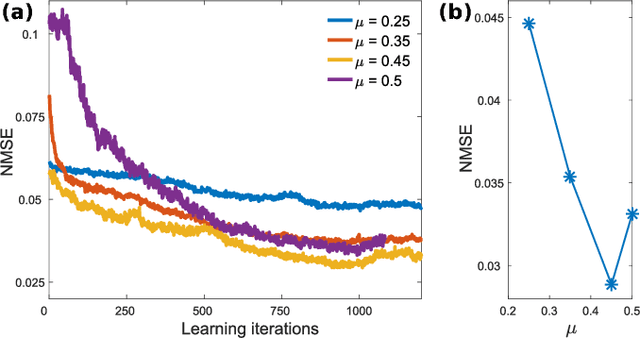
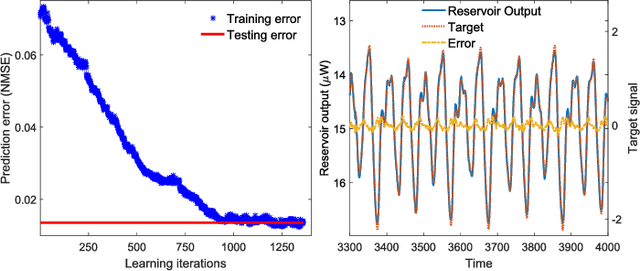
Photonic Neural Network implementations have been gaining considerable attention as a potentially disruptive future technology. Demonstrating learning in large scale neural networks is essential to establish photonic machine learning substrates as viable information processing systems. Realizing photonic Neural Networks with numerous nonlinear nodes in a fully parallel and efficient learning hardware was lacking so far. We demonstrate a network of up to 2500 diffractively coupled photonic nodes, forming a large scale Recurrent Neural Network. Using a Digital Micro Mirror Device, we realize reinforcement learning. Our scheme is fully parallel, and the passive weights maximize energy efficiency and bandwidth. The computational output efficiently converges and we achieve very good performance.

Nonlinear memory capacity of parallel time-delay reservoir computers in the processing of multidimensional signals

This paper addresses the reservoir design problem in the context of delay-based reservoir computers for multidimensional input signals, parallel architectures, and real-time multitasking. First, an approximating reservoir model is presented in those frameworks that provides an explicit functional link between the reservoir parameters and architecture and its performance in the execution of a specific task. Second, the inference properties of the ridge regression estimator in the multivariate context is used to assess the impact of finite sample training on the decrease of the reservoir capacity. Finally, an empirical study is conducted that shows the adequacy of the theoretical results with the empirical performances exhibited by various reservoir architectures in the execution of several nonlinear tasks with multidimensional inputs. Our results confirm the robustness properties of the parallel reservoir architecture with respect to task misspecification and parameter choice that had already been documented in the literature.