Nonlinear memory capacity of parallel time-delay reservoir computers in the processing of multidimensional signals

This paper addresses the reservoir design problem in the context of delay-based reservoir computers for multidimensional input signals, parallel architectures, and real-time multitasking. First, an approximating reservoir model is presented in those frameworks that provides an explicit functional link between the reservoir parameters and architecture and its performance in the execution of a specific task. Second, the inference properties of the ridge regression estimator in the multivariate context is used to assess the impact of finite sample training on the decrease of the reservoir capacity. Finally, an empirical study is conducted that shows the adequacy of the theoretical results with the empirical performances exhibited by various reservoir architectures in the execution of several nonlinear tasks with multidimensional inputs. Our results confirm the robustness properties of the parallel reservoir architecture with respect to task misspecification and parameter choice that had already been documented in the literature.

Quantitative evaluation of the performance of discrete-time reservoir computers in the forecasting, filtering, and reconstruction of stochastic stationary signals

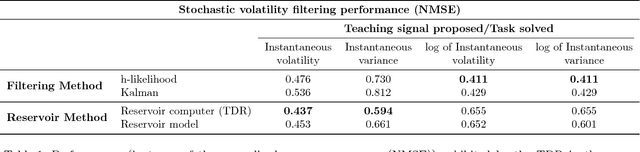
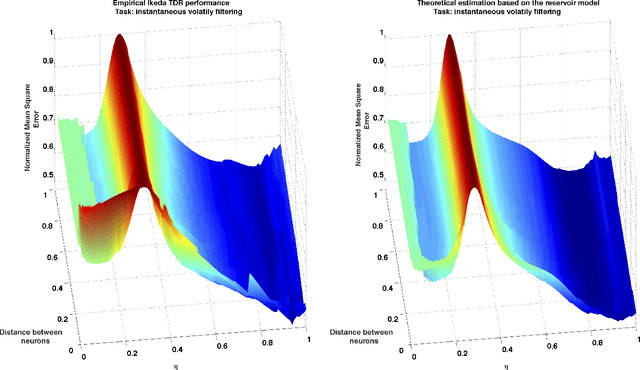
This paper extends the notion of information processing capacity for non-independent input signals in the context of reservoir computing (RC). The presence of input autocorrelation makes worthwhile the treatment of forecasting and filtering problems for which we explicitly compute this generalized capacity as a function of the reservoir parameter values using a streamlined model. The reservoir model leading to these developments is used to show that, whenever that approximation is valid, this computational paradigm satisfies the so called separation and fading memory properties that are usually associated with good information processing performances. We show that several standard memory, forecasting, and filtering problems that appear in the parametric stochastic time series context can be readily formulated and tackled via RC which, as we show, significantly outperforms standard techniques in some instances.