Quantitative evaluation of the performance of discrete-time reservoir computers in the forecasting, filtering, and reconstruction of stochastic stationary signals
Paper and Code
Oct 07, 2015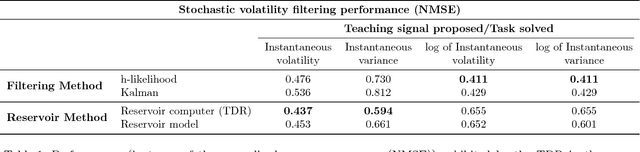
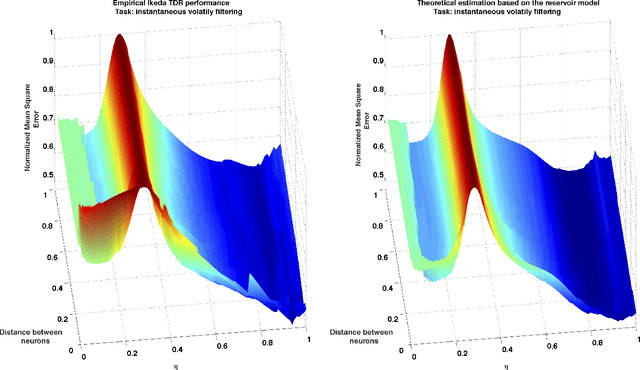
This paper extends the notion of information processing capacity for non-independent input signals in the context of reservoir computing (RC). The presence of input autocorrelation makes worthwhile the treatment of forecasting and filtering problems for which we explicitly compute this generalized capacity as a function of the reservoir parameter values using a streamlined model. The reservoir model leading to these developments is used to show that, whenever that approximation is valid, this computational paradigm satisfies the so called separation and fading memory properties that are usually associated with good information processing performances. We show that several standard memory, forecasting, and filtering problems that appear in the parametric stochastic time series context can be readily formulated and tackled via RC which, as we show, significantly outperforms standard techniques in some instances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge