Conformal Online Learning of Deep Koopman Linear Embeddings

We introduce Conformal Online Learning of Koopman embeddings (COLoKe), a novel framework for adaptively updating Koopman-invariant representations of nonlinear dynamical systems from streaming data. Our modeling approach combines deep feature learning with multistep prediction consistency in the lifted space, where the dynamics evolve linearly. To prevent overfitting, COLoKe employs a conformal-style mechanism that shifts the focus from evaluating the conformity of new states to assessing the consistency of the current Koopman model. Updates are triggered only when the current model's prediction error exceeds a dynamically calibrated threshold, allowing selective refinement of the Koopman operator and embedding. Empirical results on benchmark dynamical systems demonstrate the effectiveness of COLoKe in maintaining long-term predictive accuracy while significantly reducing unnecessary updates and avoiding overfitting.

Detecting malignant dynamics on very few blood sample using signature coefficients

Recent discoveries have suggested that the promising avenue of using circulating tumor DNA (ctDNA) levels in blood samples provides reasonable accuracy for cancer monitoring, with extremely low burden on the patient's side. It is known that the presence of ctDNA can result from various mechanisms leading to DNA release from cells, such as apoptosis, necrosis or active secretion. One key idea in recent cancer monitoring studies is that monitoring the dynamics of ctDNA levels might be sufficient for early multi-cancer detection. This interesting idea has been turned into commercial products, e.g. in the company named GRAIL. In the present work, we propose to explore the use of Signature theory for detecting aggressive cancer tumors based on the analysis of blood samples. Our approach combines tools from continuous time Markov modelling for the dynamics of ctDNA levels in the blood, with Signature theory for building efficient testing procedures. Signature theory is a topic of growing interest in the Machine Learning community (see Chevyrev2016 and Fermanian2021), which is now recognised as a powerful feature extraction tool for irregularly sampled signals. The method proposed in the present paper is shown to correctly address the challenging problem of overcoming the inherent data scarsity due to the extremely small number of blood samples per patient. The relevance of our approach is illustrated with extensive numerical experiments that confirm the efficiency of the proposed pipeline.

Registration of algebraic varieties using Riemannian optimization

We consider the point cloud registration problem, the task of finding a transformation between two point clouds that represent the same object but are expressed in different coordinate systems. Our approach is not based on a point-to-point correspondence, matching every point in the source point cloud to a point in the target point cloud. Instead, we assume and leverage a low-dimensional nonlinear geometric structure of the data. Firstly, we approximate each point cloud by an algebraic variety (a set defined by finitely many polynomial equations). This is done by solving an optimization problem on the Grassmann manifold, using a connection between algebraic varieties and polynomial bases. Secondly, we solve an optimization problem on the orthogonal group to find the transformation (rotation $+$ translation) which makes the two algebraic varieties overlap. We use second-order Riemannian optimization methods for the solution of both steps. Numerical experiments on real and synthetic data are provided, with encouraging results. Our approach is particularly useful when the two point clouds describe different parts of an objects (which may not even be overlapping), on the condition that the surface of the object may be well approximated by a set of polynomial equations. The first procedure -- the approximation -- is of independent interest, as it can be used for denoising data that belongs to an algebraic variety. We provide statistical guarantees for the estimation error of the denoising using Stein's unbiased estimator.

Convergence and scaling of Boolean-weight optimization for hardware reservoirs

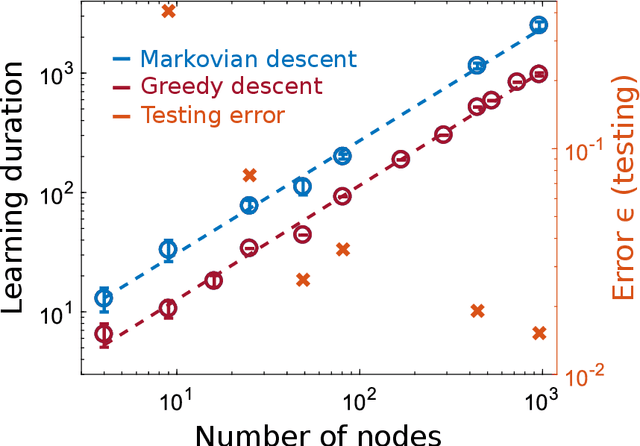
Hardware implementation of neural network are an essential step to implement next generation efficient and powerful artificial intelligence solutions. Besides the realization of a parallel, efficient and scalable hardware architecture, the optimization of the system's extremely large parameter space with sampling-efficient approaches is essential. Here, we analytically derive the scaling laws for highly efficient Coordinate Descent applied to optimizing the readout layer of a random recurrently connection neural network, a reservoir. We demonstrate that the convergence is exponential and scales linear with the network's number of neurons. Our results perfectly reproduce the convergence and scaling of a large-scale photonic reservoir implemented in a proof-of-concept experiment. Our work therefore provides a solid foundation for such optimization in hardware networks, and identifies future directions that are promising for optimizing convergence speed during learning leveraging measures of a neural network's amplitude statistics and the weight update rule.

Boolean learning under noise-perturbations in hardware neural networks

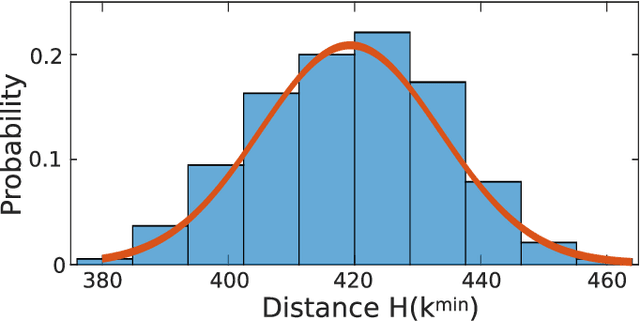
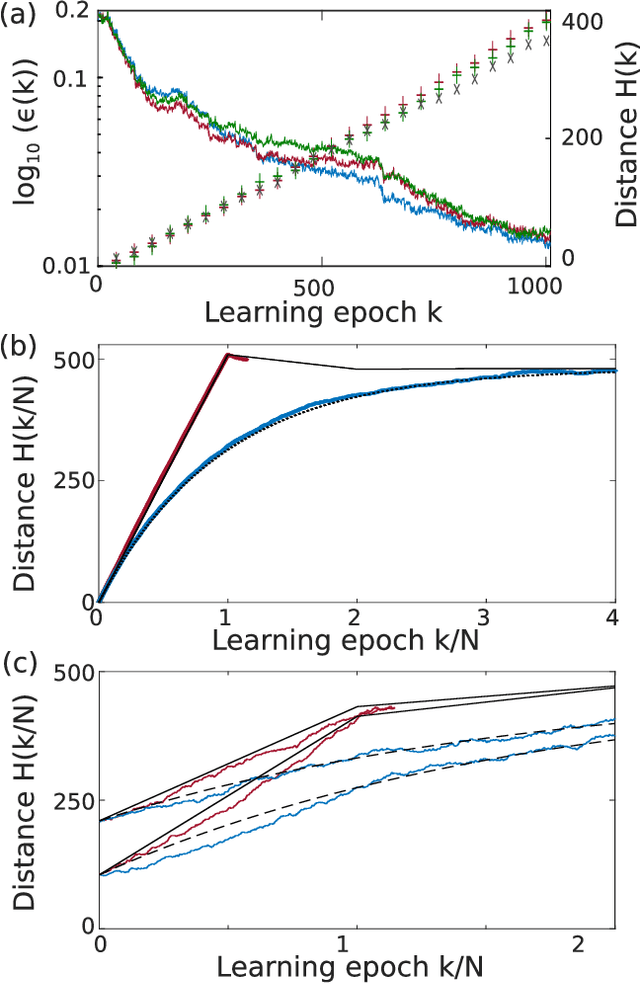
A high efficiency hardware integration of neural networks benefits from realizing nonlinearity, network connectivity and learning fully in a physical substrate. Multiple systems have recently implemented some or all of these operations, yet the focus was placed on addressing technological challenges. Fundamental questions regarding learning in hardware neural networks remain largely unexplored. Noise in particular is unavoidable in such architectures, and here we investigate its interaction with a learning algorithm using an opto-electronic recurrent neural network. We find that noise strongly modifies the system's path during convergence, and surprisingly fully decorrelates the final readout weight matrices. This highlights the importance of understanding architecture, noise and learning algorithm as interacting players, and therefore identifies the need for mathematical tools for noisy, analogue system optimization.

Revisiting clustering as matrix factorisation on the Stiefel manifold

This paper studies clustering for possibly high dimensional data (\emph{e.g.} images, time series, gene expression data, and many other settings), and rephrase it as low rank matrix estimation in the PAC-Bayesian framework. Our approach leverages the well known Burer-Monteiro factorisation strategy from large scale optimisation, in the context of low rank estimation. Moreover, our Burer-Monteiro factors are shown to lie on a Stiefel manifold. We propose a new generalized Bayesian estimator for this problem and prove novel prediction bounds for clustering. We also devise a componentwise Langevin sampler on the Stiefel manifold to compute this estimator.

Finding optimal finite biological sequences over finite alphabets: the OptiFin toolbox

In this paper, we present a toolbox for a specific optimization problem that frequently arises in bioinformatics or genomics. In this specific optimisation problem, the state space is a set of words of specified length over a finite alphabet. To each word is associated a score. The overall objective is to find the words which have the lowest possible score. This type of general optimization problem is encountered in e.g 3D conformation optimisation for protein structure prediction, or largest core genes subset discovery based on best supported phylogenetic tree for a set of species. In order to solve this problem, we propose a toolbox that can be easily launched using MPI and embeds 3 well-known metaheuristics. The toolbox is fully parametrized and well documented. It has been specifically designed to be easy modified and possibly improved by the user depending on the application, and does not require to be a computer scientist. We show that the toolbox performs very well on two difficult practical problems.

Small coherence implies the weak Null Space Property

In the Compressed Sensing community, it is well known that given a matrix $X \in \mathbb R^{n\times p}$ with $\ell_2$ normalized columns, the Restricted Isometry Property (RIP) implies the Null Space Property (NSP). It is also well known that a small Coherence $\mu$ implies a weak RIP, i.e. the singular values of $X_T$ lie between $1-\delta$ and $1+\delta$ for "most" index subsets $T \subset \{1,\ldots,p\}$ with size governed by $\mu$ and $\delta$. In this short note, we show that a small Coherence implies a weak Null Space Property, i.e. $\Vert h_T\Vert_2 \le C \ \Vert h_{T^c}\Vert_1/\sqrt{s}$ for most $T \subset \{1,\ldots,p\}$ with cardinality $|T|\le s$. We moreover prove some singular value perturbation bounds that may also prove useful for other applications.

A Semi-Definite Programming approach to low dimensional embedding for unsupervised clustering

This paper proposes a variant of the method of Gu\'edon and Verhynin for estimating the cluster matrix in the Mixture of Gaussians framework via Semi-Definite Programming. A clustering oriented embedding is deduced from this estimate. The procedure is suitable for very high dimensional data because it is based on pairwise distances only. Theoretical garantees are provided and an eigenvalue optimisation approach is proposed for computing the embedding. The performance of the method is illustrated via Monte Carlo experiements and comparisons with other embeddings from the literature.

Sparse recovery with unknown variance: a LASSO-type approach

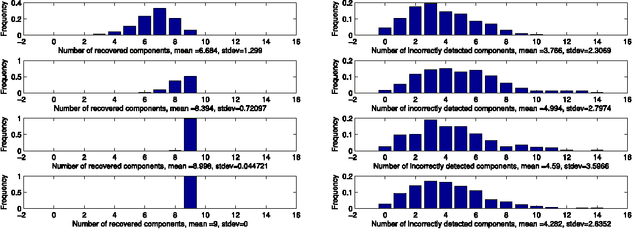
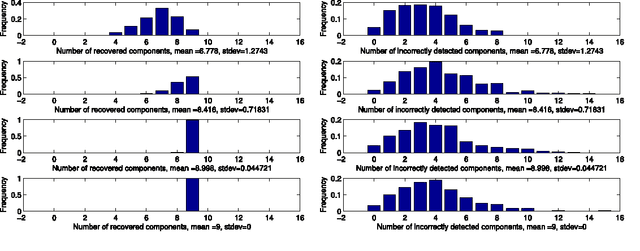
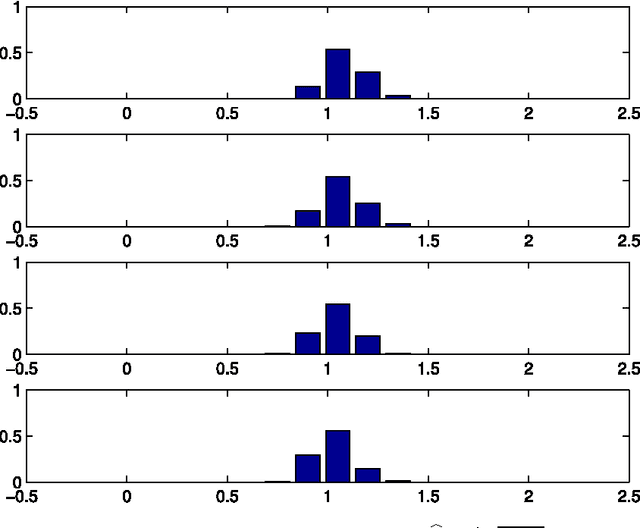
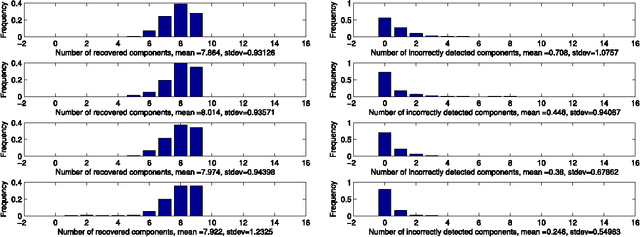
We address the issue of estimating the regression vector $\beta$ in the generic $s$-sparse linear model $y = X\beta+z$, with $\beta\in\R^{p}$, $y\in\R^{n}$, $z\sim\mathcal N(0,\sg^2 I)$ and $p> n$ when the variance $\sg^{2}$ is unknown. We study two LASSO-type methods that jointly estimate $\beta$ and the variance. These estimators are minimizers of the $\ell_1$ penalized least-squares functional, where the relaxation parameter is tuned according to two different strategies. In the first strategy, the relaxation parameter is of the order $\ch{\sigma} \sqrt{\log p}$, where $\ch{\sigma}^2$ is the empirical variance. %The resulting optimization problem can be solved by running only a few successive LASSO instances with %recursive updating of the relaxation parameter. In the second strategy, the relaxation parameter is chosen so as to enforce a trade-off between the fidelity and the penalty terms at optimality. For both estimators, our assumptions are similar to the ones proposed by Cand\`es and Plan in {\it Ann. Stat. (2009)}, for the case where $\sg^{2}$ is known. We prove that our estimators ensure exact recovery of the support and sign pattern of $\beta$ with high probability. We present simulations results showing that the first estimator enjoys nearly the same performances in practice as the standard LASSO (known variance case) for a wide range of the signal to noise ratio. Our second estimator is shown to outperform both in terms of false detection, when the signal to noise ratio is low.