Distributional Regression U-Nets for the Postprocessing of Precipitation Ensemble Forecasts

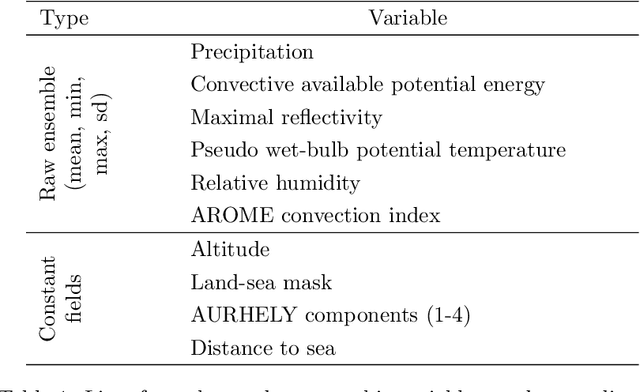
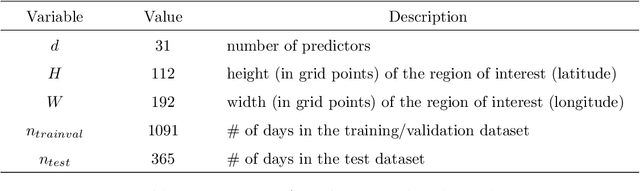
Accurate precipitation forecasts have a high socio-economic value due to their role in decision-making in various fields such as transport networks and farming. We propose a global statistical postprocessing method for grid-based precipitation ensemble forecasts. This U-Net-based distributional regression method predicts marginal distributions in the form of parametric distributions inferred by scoring rule minimization. Distributional regression U-Nets are compared to state-of-the-art postprocessing methods for daily 21-h forecasts of 3-h accumulated precipitation over the South of France. Training data comes from the M\'et\'eo-France weather model AROME-EPS and spans 3 years. A practical challenge appears when consistent data or reforecasts are not available. Distributional regression U-Nets compete favorably with the raw ensemble. In terms of continuous ranked probability score, they reach a performance comparable to quantile regression forests (QRF). However, they are unable to provide calibrated forecasts in areas associated with high climatological precipitation. In terms of predictive power for heavy precipitation events, they outperform both QRF and semi-parametric QRF with tail extensions.

A new methodology to predict the oncotype scores based on clinico-pathological data with similar tumor profiles

Introduction: The Oncotype DX (ODX) test is a commercially available molecular test for breast cancer assay that provides prognostic and predictive breast cancer recurrence information for hormone positive, HER2-negative patients. The aim of this study is to propose a novel methodology to assist physicians in their decision-making. Methods: A retrospective study between 2012 and 2020 with 333 cases that underwent an ODX assay from three hospitals in Bourgogne Franche-Comt{\'e} was conducted. Clinical and pathological reports were used to collect the data. A methodology based on distributional random forest was developed using 9 clinico-pathological characteristics. This methodology can be used particularly to identify the patients of the training cohort that share similarities with the new patient and to predict an estimate of the distribution of the ODX score. Results: The mean age of participants id 56.9 years old. We have correctly classified 92% of patients in low risk and 40.2% of patients in high risk. The overall accuracy is 79.3%. The proportion of low risk correct predicted value (PPV) is 82%. The percentage of high risk correct predicted value (NPV) is approximately 62.3%. The F1-score and the Area Under Curve (AUC) are of 0.87 and 0.759, respectively. Conclusion: The proposed methodology makes it possible to predict the distribution of the ODX score for a patient and provides an explanation of the predicted score. The use of the methodology with the pathologist's expertise on the different histological and immunohistochemical characteristics has a clinical impact to help oncologist in decision-making regarding breast cancer therapy.

Mathematical Properties of Continuous Ranked Probability Score Forecasting

The theoretical advances on the properties of scoring rules over the past decades have broaden the use of scoring rules in probabilistic forecasting. In meteorological forecasting, statistical postprocessing techniques are essential to improve the forecasts made by deterministic physical models. Numerous state-of-the-art statistical postprocessing techniques are based on distributional regression evaluated with the Continuous Ranked Probability Score (CRPS). However, theoretical properties of such minimization of the CRPS have mostly considered the unconditional framework (i.e. without covariables) and infinite sample sizes. We circumvent these limitations and study the rate of convergence in terms of CRPS of distributional regression methods We find the optimal minimax rate of convergence for a given class of distributions. Moreover, we show that the k-nearest neighbor method and the kernel method for the distributional regression reach the optimal rate of convergence in dimension $d\geq2$ and in any dimension, respectively.

Infinitesimal gradient boosting

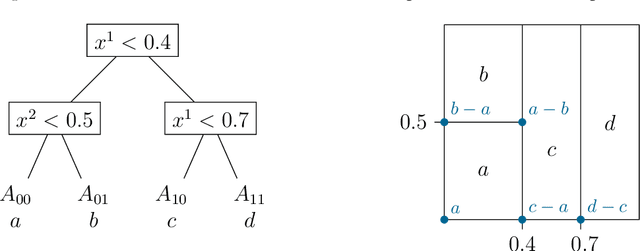
We define infinitesimal gradient boosting as a limit of the popular tree-based gradient boosting algorithm from machine learning. The limit is considered in the vanishing-learning-rate asymptotic, that is when the learning rate tends to zero and the number of gradient trees is rescaled accordingly. For this purpose, we introduce a new class of randomized regression trees bridging totally randomized trees and Extra Trees and using a softmax distribution for binary splitting. Our main result is the convergence of the associated stochastic algorithm and the characterization of the limiting procedure as the unique solution of a nonlinear ordinary differential equation in a infinite dimensional function space. Infinitesimal gradient boosting defines a smooth path in the space of continuous functions along which the training error decreases, the residuals remain centered and the total variation is well controlled.

Behavior of linear L2-boosting algorithms in the vanishing learning rate asymptotic

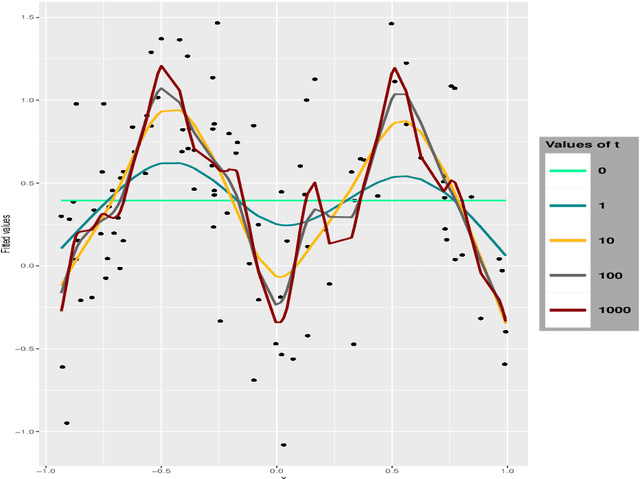
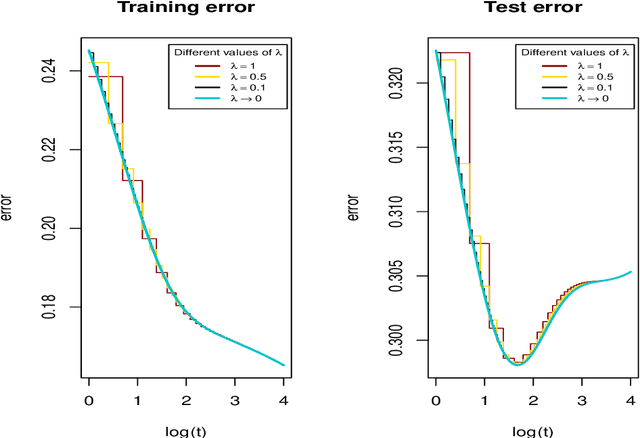
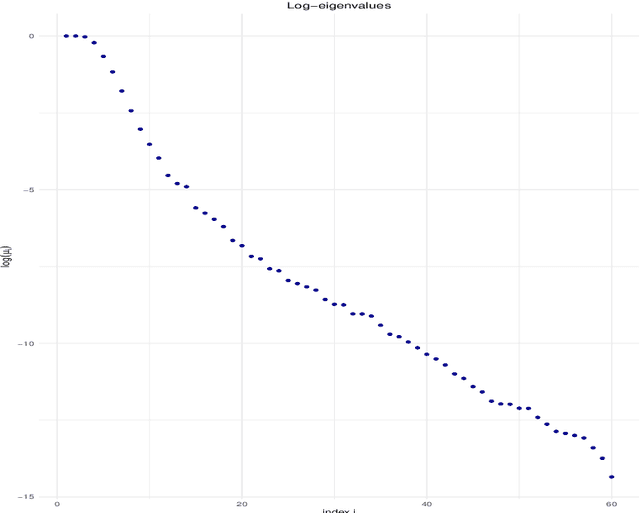
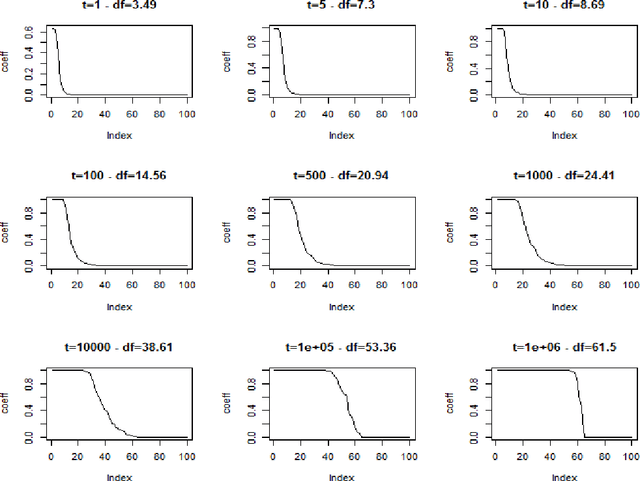
We investigate the asymptotic behaviour of gradient boosting algorithms when the learning rate converges to zero and the number of iterations is rescaled accordingly. We mostly consider L2-boosting for regression with linear base learner as studied in B{\"u}hlmann and Yu (2003) and analyze also a stochastic version of the model where subsampling is used at each step (Friedman 2002). We prove a deterministic limit in the vanishing learning rate asymptotic and characterize the limit as the unique solution of a linear differential equation in an infinite dimensional function space. Besides, the training and test error of the limiting procedure are thoroughly analyzed. We finally illustrate and discuss our result on a simple numerical experiment where the linear L2-boosting operator is interpreted as a smoothed projection and time is related to its number of degrees of freedom.

A Semi-Definite Programming approach to low dimensional embedding for unsupervised clustering

This paper proposes a variant of the method of Gu\'edon and Verhynin for estimating the cluster matrix in the Mixture of Gaussians framework via Semi-Definite Programming. A clustering oriented embedding is deduced from this estimate. The procedure is suitable for very high dimensional data because it is based on pairwise distances only. Theoretical garantees are provided and an eigenvalue optimisation approach is proposed for computing the embedding. The performance of the method is illustrated via Monte Carlo experiements and comparisons with other embeddings from the literature.