Behavior of linear L2-boosting algorithms in the vanishing learning rate asymptotic
Paper and Code
Dec 29, 2020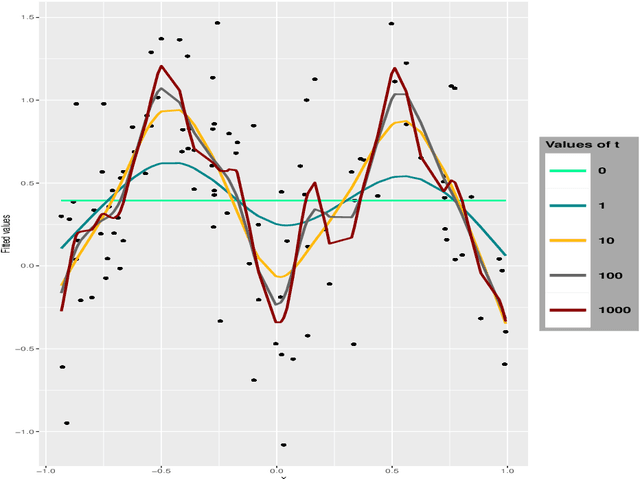
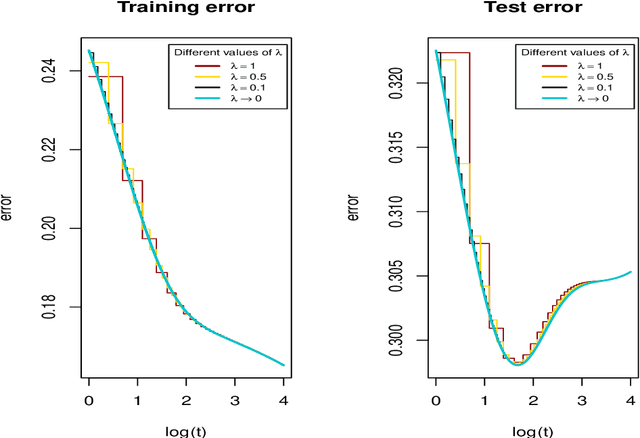
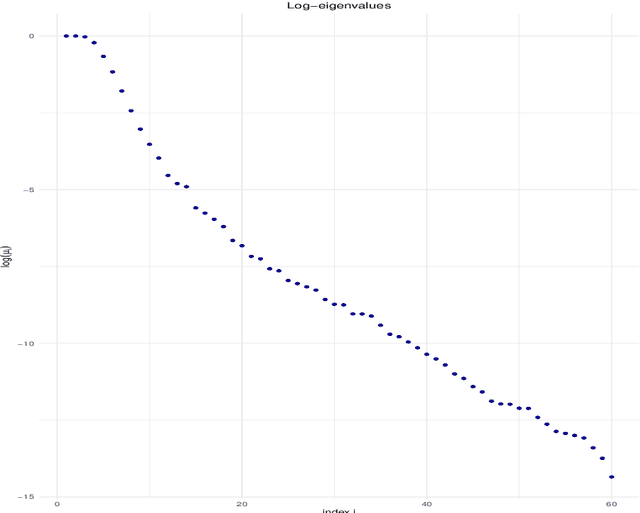
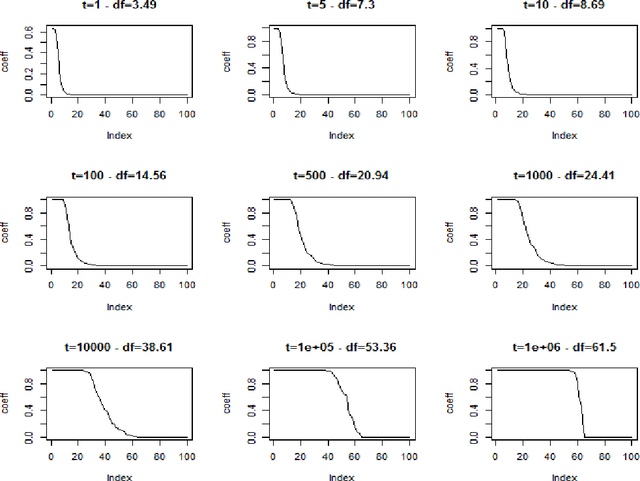
We investigate the asymptotic behaviour of gradient boosting algorithms when the learning rate converges to zero and the number of iterations is rescaled accordingly. We mostly consider L2-boosting for regression with linear base learner as studied in B{\"u}hlmann and Yu (2003) and analyze also a stochastic version of the model where subsampling is used at each step (Friedman 2002). We prove a deterministic limit in the vanishing learning rate asymptotic and characterize the limit as the unique solution of a linear differential equation in an infinite dimensional function space. Besides, the training and test error of the limiting procedure are thoroughly analyzed. We finally illustrate and discuss our result on a simple numerical experiment where the linear L2-boosting operator is interpreted as a smoothed projection and time is related to its number of degrees of freedom.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge