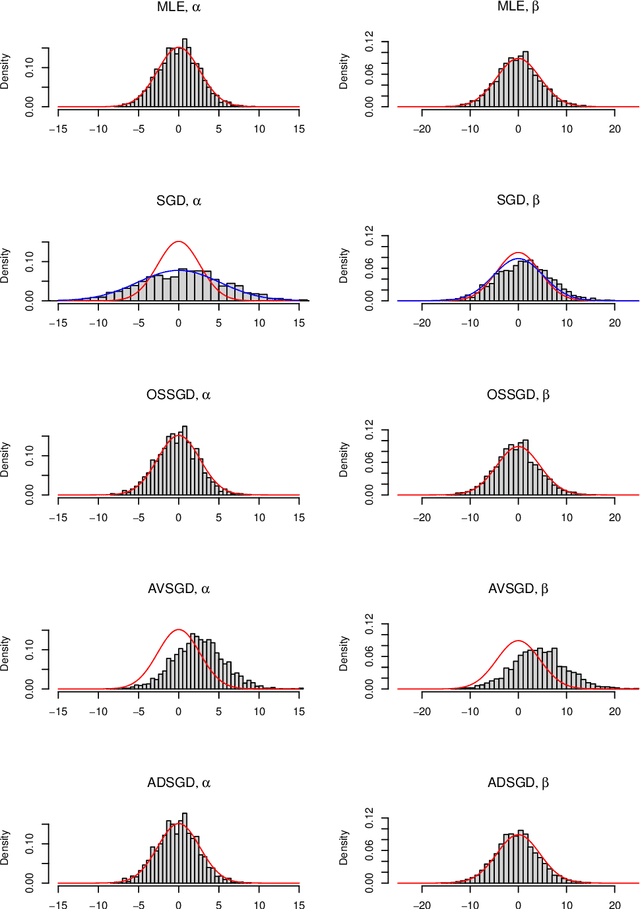
Asymptotically efficient one-step stochastic gradient descent

A generic, fast and asymptotically efficient method for parametric estimation is described. It is based on the stochastic gradient descent on the loglikelihood function corrected by a single step of the Fisher scoring algorithm. We show theoretically and by simulations in the i.i.d. setting that it is an interesting alternative to the usual stochastic gradient descent with averaging or the adaptative stochastic gradient descent.

Behavior of linear L2-boosting algorithms in the vanishing learning rate asymptotic

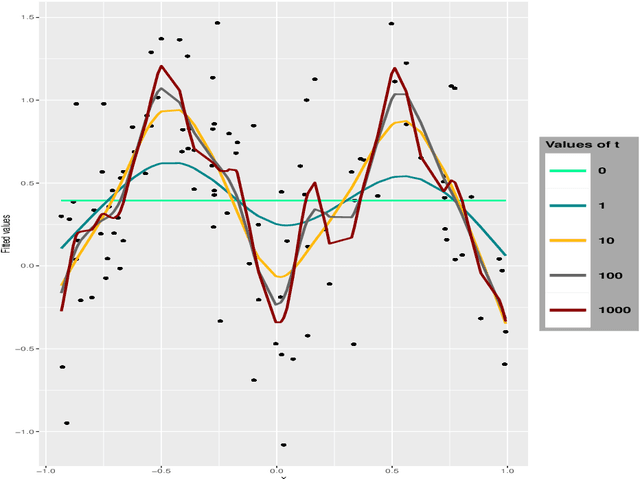
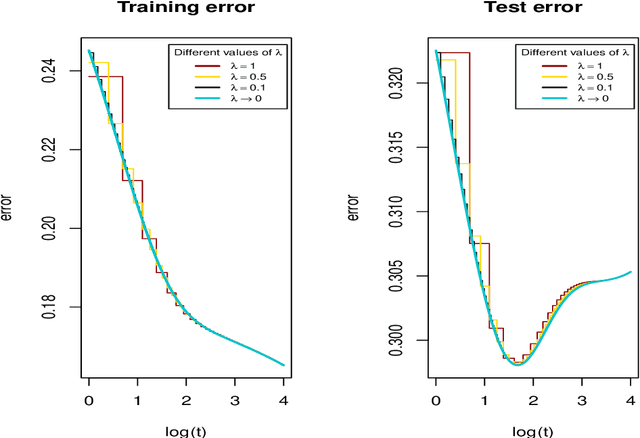
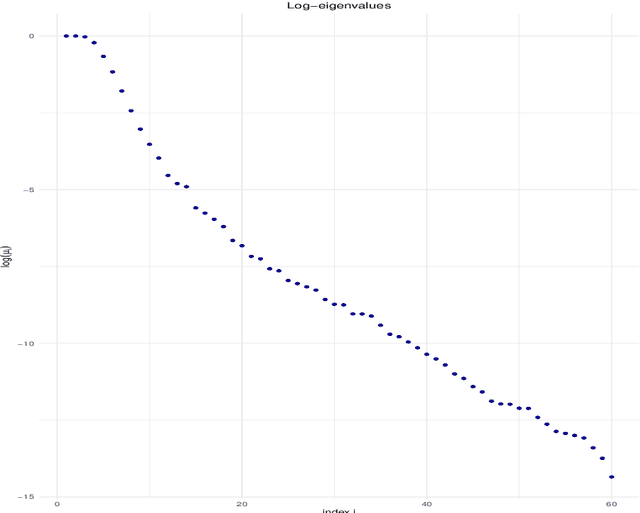
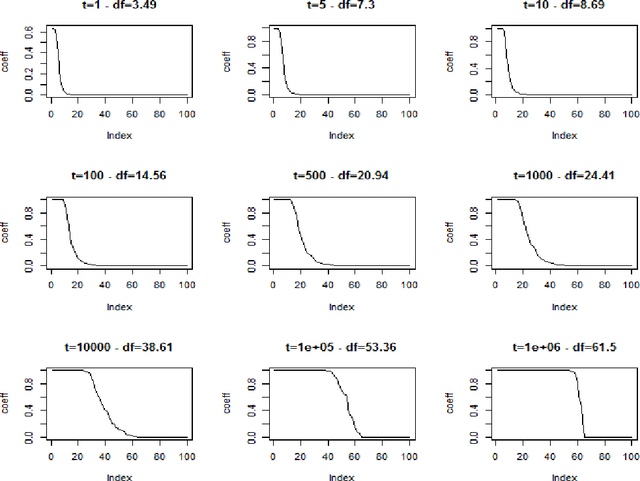
We investigate the asymptotic behaviour of gradient boosting algorithms when the learning rate converges to zero and the number of iterations is rescaled accordingly. We mostly consider L2-boosting for regression with linear base learner as studied in B{\"u}hlmann and Yu (2003) and analyze also a stochastic version of the model where subsampling is used at each step (Friedman 2002). We prove a deterministic limit in the vanishing learning rate asymptotic and characterize the limit as the unique solution of a linear differential equation in an infinite dimensional function space. Besides, the training and test error of the limiting procedure are thoroughly analyzed. We finally illustrate and discuss our result on a simple numerical experiment where the linear L2-boosting operator is interpreted as a smoothed projection and time is related to its number of degrees of freedom.

Diagnostic checking in FARIMA models with uncorrelated but non-independent error terms

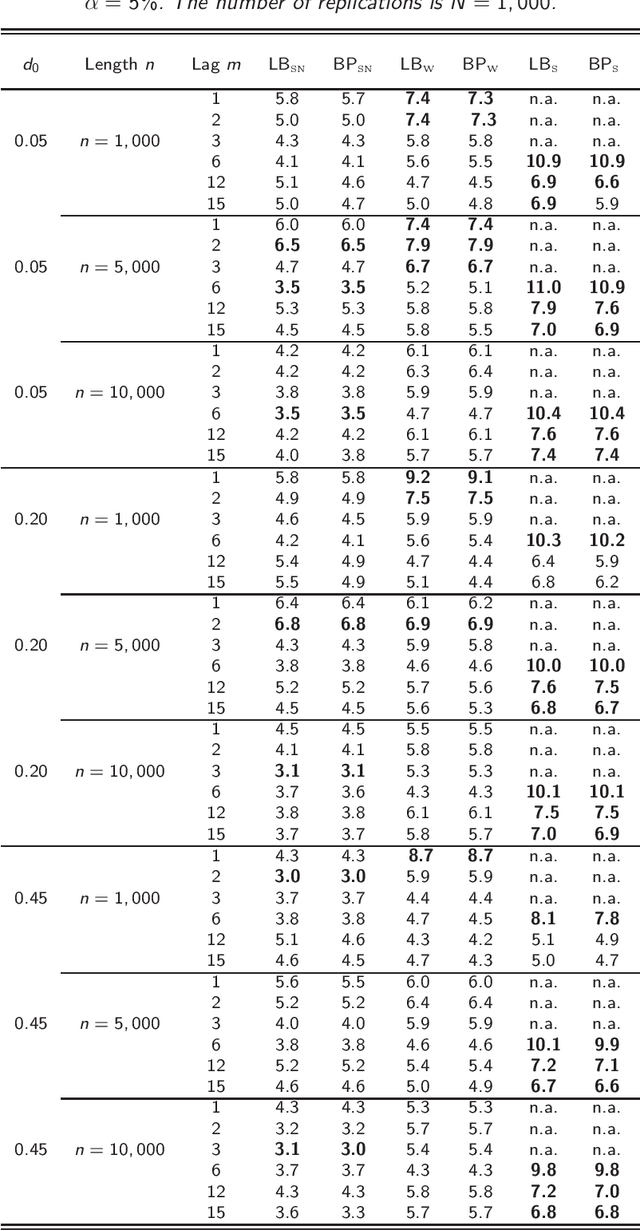
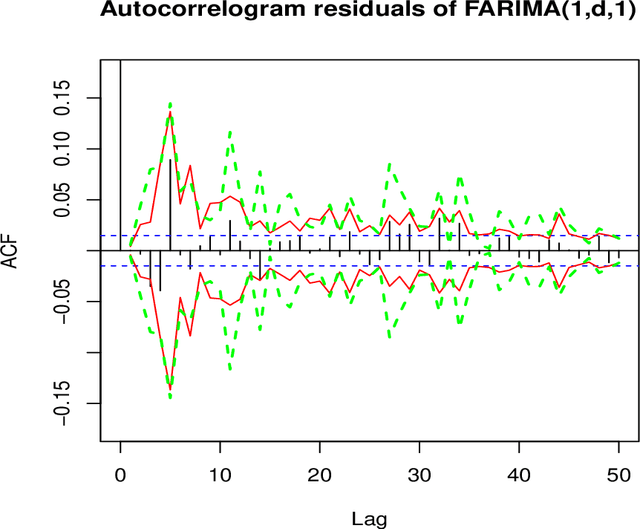
This work considers the problem of modified portmanteau tests for testing the adequacy of FARIMA models under the assumption that the errors are uncorrelated but not necessarily independent (i.e. weak FARIMA). We first study the joint distribution of the least squares estimator and the noise empirical autocovariances. We then derive the asymp-totic distribution of residual empirical autocovariances and autocorrelations. We deduce the asymptotic distribution of the Ljung-Box (or Box-Pierce) modified portmanteau statistics for weak FARIMA models. We also propose another method based on a self-normalization approach to test the adequacy of FARIMA models. Finally some simulation studies are presented to corroborate our theoretical work. An application to the Standard \& Poor's 500 and Nikkei returns also illustrate the practical relevance of our theoretical results. AMS 2000 subject classifications: Primary 62M10, 62F03, 62F05; secondary 91B84, 62P05.