Diagnostic checking in FARIMA models with uncorrelated but non-independent error terms

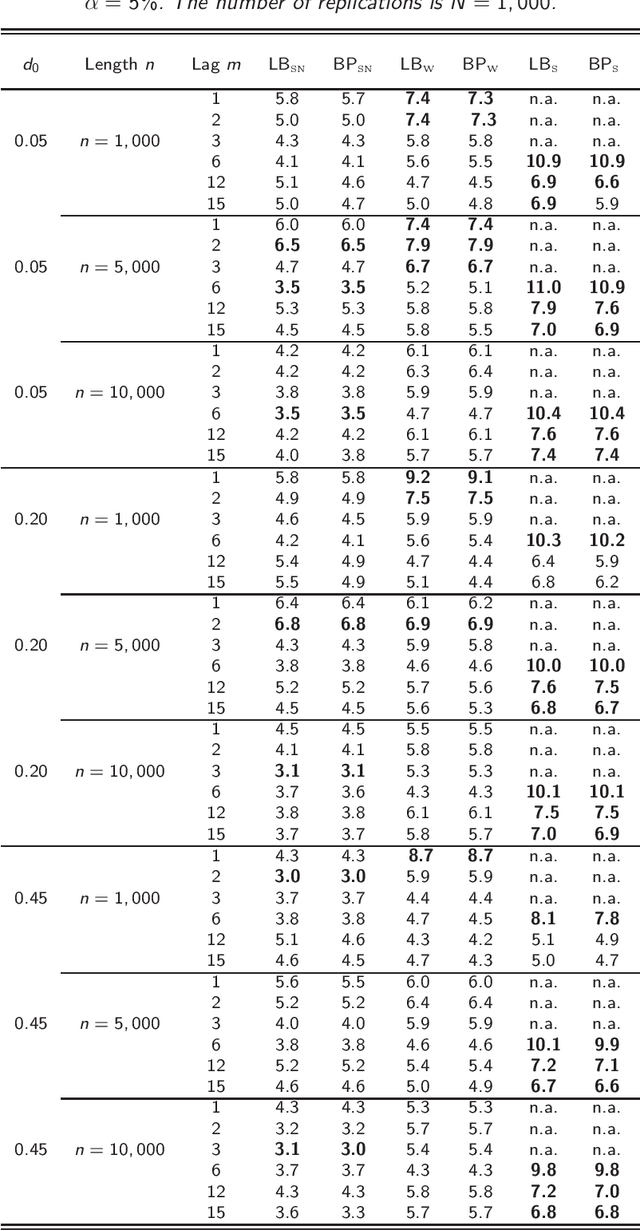
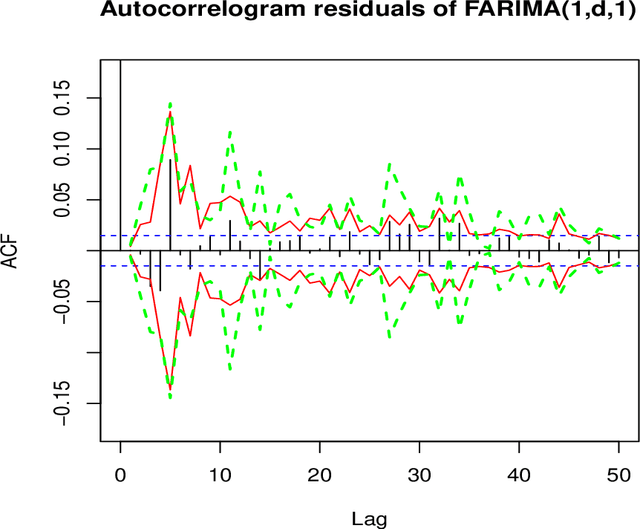
This work considers the problem of modified portmanteau tests for testing the adequacy of FARIMA models under the assumption that the errors are uncorrelated but not necessarily independent (i.e. weak FARIMA). We first study the joint distribution of the least squares estimator and the noise empirical autocovariances. We then derive the asymp-totic distribution of residual empirical autocovariances and autocorrelations. We deduce the asymptotic distribution of the Ljung-Box (or Box-Pierce) modified portmanteau statistics for weak FARIMA models. We also propose another method based on a self-normalization approach to test the adequacy of FARIMA models. Finally some simulation studies are presented to corroborate our theoretical work. An application to the Standard \& Poor's 500 and Nikkei returns also illustrate the practical relevance of our theoretical results. AMS 2000 subject classifications: Primary 62M10, 62F03, 62F05; secondary 91B84, 62P05.

Estimation of multivariate asymmetric power GARCH models

It is now widely accepted that volatility models have to incorporate the so-called leverage effect in order to to model the dynamics of daily financial returns.We suggest a new class of multivariate power transformed asymmetric models. It includes several functional forms of multivariate GARCH models which are of great interest in financial modeling and time series literature. We provide an explicit necessary and sufficient condition to establish the strict stationarity of the model. We derive the asymptotic properties of the quasi-maximum likelihood estimator of the parameters. These properties are established both when the power of the transformation is known or is unknown. The asymptotic results are illustrated by Monte Carlo experiments. An application to real financial data is also proposed.

Portmanteau test for the asymmetric power GARCH model when the power is unknown

It is now widely accepted that, to model the dynamics of daily financial returns, volatility models have to incorporate the so-called leverage effect. We derive the asymptotic behaviour of the squared residuals autocovariances for the class of asymmetric power GARCH model when the power is unknown and is jointly estimated with the model's parameters. We then deduce a portmanteau adequacy test based on the autocovariances of the squared residuals. These asymptotic results are illustrated by Monte Carlo experiments. An application to real financial data is also proposed.