Inferring untrained complex dynamics of delay systems using an adapted echo state network

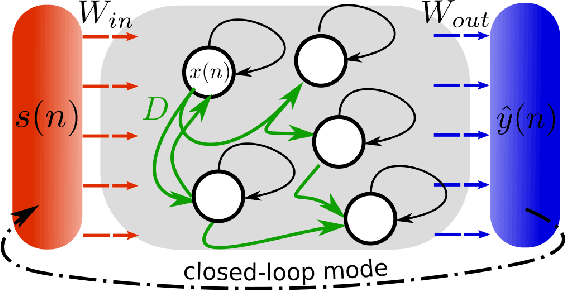
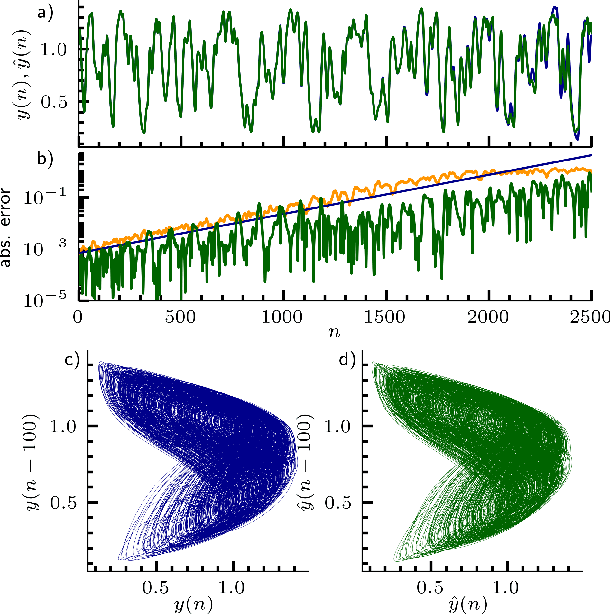
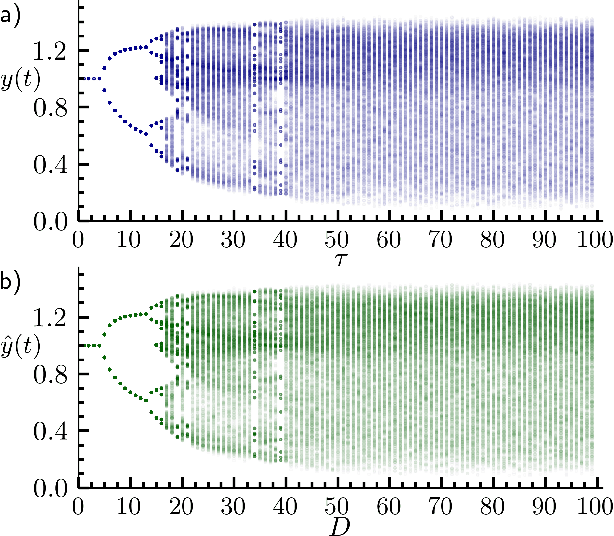
Caused by finite signal propagation velocities, many complex systems feature time delays that may induce high-dimensional chaotic behavior and make forecasting intricate. Here, we propose an echo state network adaptable to the physics of systems with arbitrary delays. After training the network to forecast a system with a unique and sufficiently long delay, it already learned to predict the system dynamics for all other delays. A simple adaptation of the network's topology allows us to infer untrained features such as high-dimensional chaotic attractors, bifurcations, and even multistabilities, that emerge with shorter and longer delays. Thus, the fusion of physical knowledge of the delay system and data-driven machine learning yields a model with high generalization capabilities and unprecedented prediction accuracy.

Microring resonators with external optical feedback for time delay reservoir computing

Microring resonators (MRRs) are a key photonic component in integrated devices, due to their small size, low insertion losses, and passive operation. While the MRRs have been established for optical filtering in wavelength-multiplexed systems, the nonlinear properties that they can exhibit give rise to new perspectives on their use. For instance, they have been recently considered for introducing optical nonlinearity in photonic reservoir computing systems. In this work, we present a detailed numerical investigation of a silicon MRR operation, in the presence of external optical feedback, in a time delay reservoir computing scheme. We demonstrate the versatility of this compact, passive device, by exploiting different operating regimes and solving computing tasks with diverse memory requirements. We show that when large memory is required, as it occurs in the Narma 10 task, the MRR nonlinearity does not play a significant role when the photodetection nonlinearity is involved, while the contribution of the external feedback is significant. On the contrary, for computing tasks such as the Mackey-Glass and the Santa Fe chaotic timeseries prediction, the MRR and the photodetection nonlinearities contribute both to efficient computation. The presence of optical feedback improves the prediction of the Mackey-Glass timeseries while plays a minor role in the Santa Fe timeseries case.

Unveiling the role of plasticity rules in reservoir computing

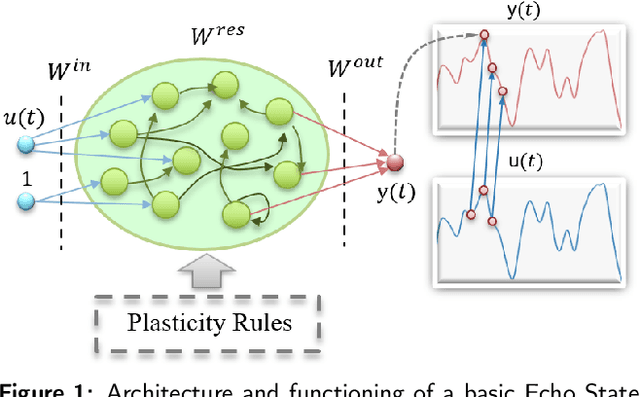
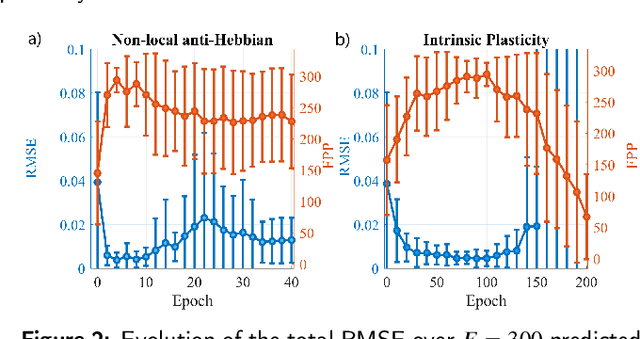
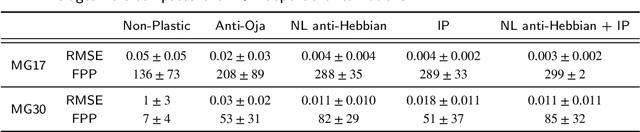
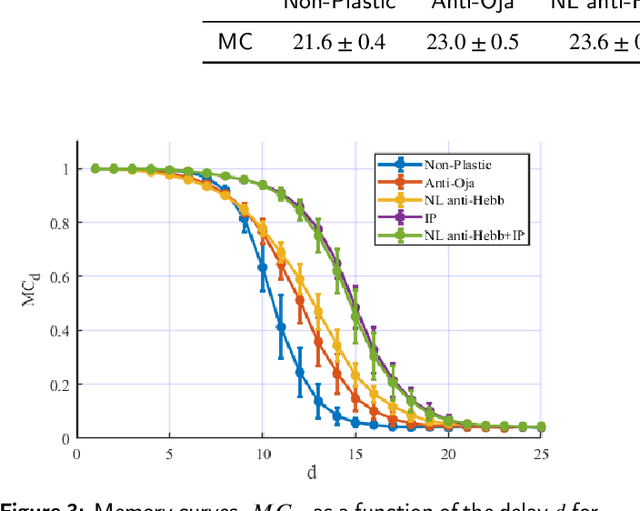
Reservoir Computing (RC) is an appealing approach in Machine Learning that combines the high computational capabilities of Recurrent Neural Networks with a fast and easy training method. Likewise, successful implementation of neuro-inspired plasticity rules into RC artificial networks has boosted the performance of the original models. In this manuscript, we analyze the role that plasticity rules play on the changes that lead to a better performance of RC. To this end, we implement synaptic and non-synaptic plasticity rules in a paradigmatic example of RC model: the Echo State Network. Testing on nonlinear time series prediction tasks, we show evidence that improved performance in all plastic models are linked to a decrease of the pair-wise correlations in the reservoir, as well as a significant increase of individual neurons ability to separate similar inputs in their activity space. Here we provide new insights on this observed improvement through the study of different stages on the plastic learning. From the perspective of the reservoir dynamics, optimal performance is found to occur close to the so-called edge of instability. Our results also show that it is possible to combine different forms of plasticity (namely synaptic and non-synaptic rules) to further improve the performance on prediction tasks, obtaining better results than those achieved with single-plasticity models.