Adaptive control of recurrent neural networks using conceptors

Recurrent Neural Networks excel at predicting and generating complex high-dimensional temporal patterns. Due to their inherent nonlinear dynamics and memory, they can learn unbounded temporal dependencies from data. In a Machine Learning setting, the network's parameters are adapted during a training phase to match the requirements of a given task/problem increasing its computational capabilities. After the training, the network parameters are kept fixed to exploit the learned computations. The static parameters thereby render the network unadaptive to changing conditions, such as external or internal perturbation. In this manuscript, we demonstrate how keeping parts of the network adaptive even after the training enhances its functionality and robustness. Here, we utilize the conceptor framework and conceptualize an adaptive control loop analyzing the network's behavior continuously and adjusting its time-varying internal representation to follow a desired target. We demonstrate how the added adaptivity of the network supports the computational functionality in three distinct tasks: interpolation of temporal patterns, stabilization against partial network degradation, and robustness against input distortion. Our results highlight the potential of adaptive networks in machine learning beyond training, enabling them to not only learn complex patterns but also dynamically adjust to changing environments, ultimately broadening their applicability.

Dynamical stability and chaos in artificial neural network trajectories along training

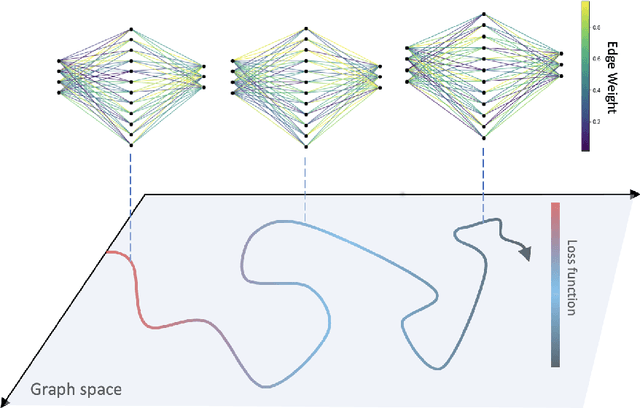
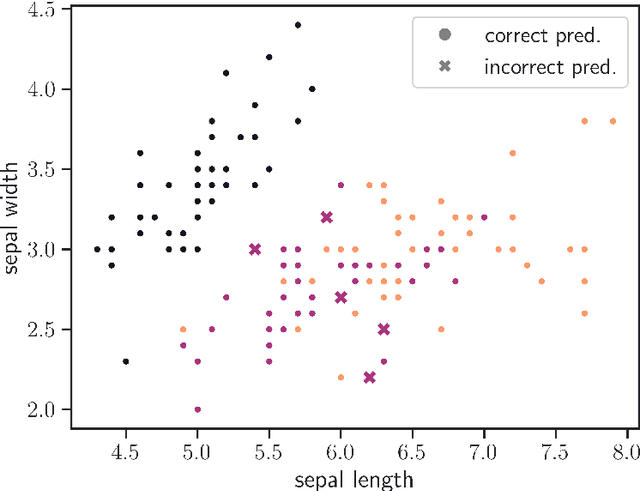
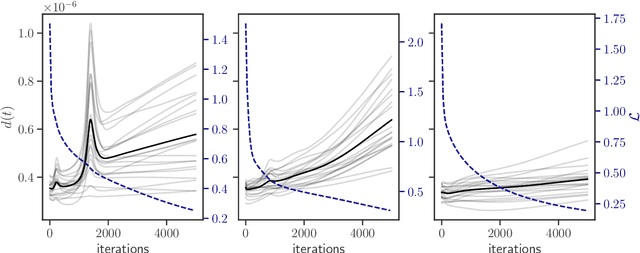
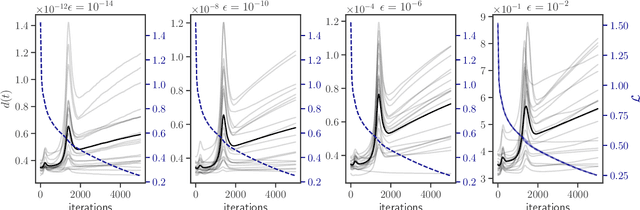
The process of training an artificial neural network involves iteratively adapting its parameters so as to minimize the error of the network's prediction, when confronted with a learning task. This iterative change can be naturally interpreted as a trajectory in network space -- a time series of networks -- and thus the training algorithm (e.g. gradient descent optimization of a suitable loss function) can be interpreted as a dynamical system in graph space. In order to illustrate this interpretation, here we study the dynamical properties of this process by analyzing through this lens the network trajectories of a shallow neural network, and its evolution through learning a simple classification task. We systematically consider different ranges of the learning rate and explore both the dynamical and orbital stability of the resulting network trajectories, finding hints of regular and chaotic behavior depending on the learning rate regime. Our findings are put in contrast to common wisdom on convergence properties of neural networks and dynamical systems theory. This work also contributes to the cross-fertilization of ideas between dynamical systems theory, network theory and machine learning

Inferring untrained complex dynamics of delay systems using an adapted echo state network

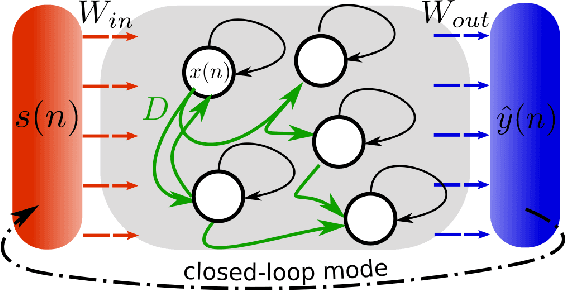
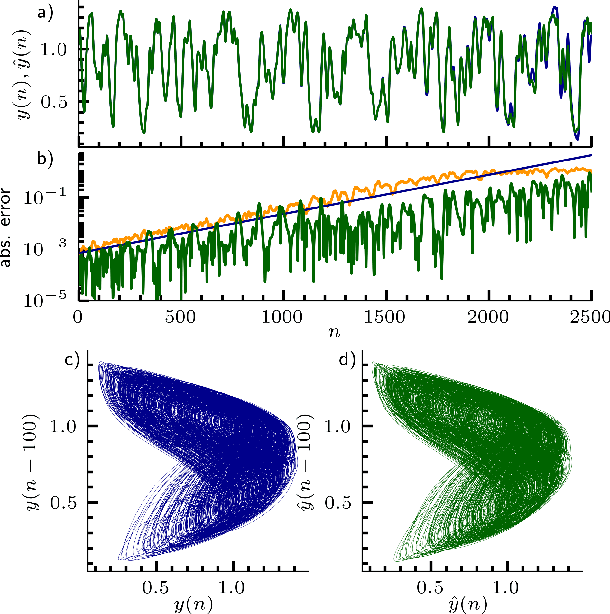
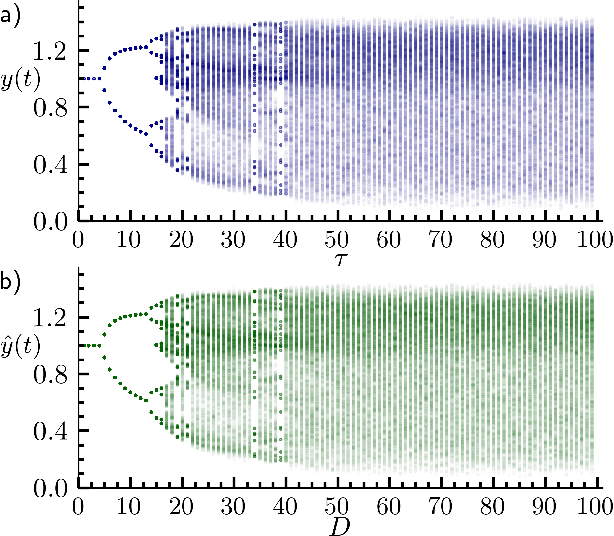
Caused by finite signal propagation velocities, many complex systems feature time delays that may induce high-dimensional chaotic behavior and make forecasting intricate. Here, we propose an echo state network adaptable to the physics of systems with arbitrary delays. After training the network to forecast a system with a unique and sufficiently long delay, it already learned to predict the system dynamics for all other delays. A simple adaptation of the network's topology allows us to infer untrained features such as high-dimensional chaotic attractors, bifurcations, and even multistabilities, that emerge with shorter and longer delays. Thus, the fusion of physical knowledge of the delay system and data-driven machine learning yields a model with high generalization capabilities and unprecedented prediction accuracy.

Unveiling the role of plasticity rules in reservoir computing

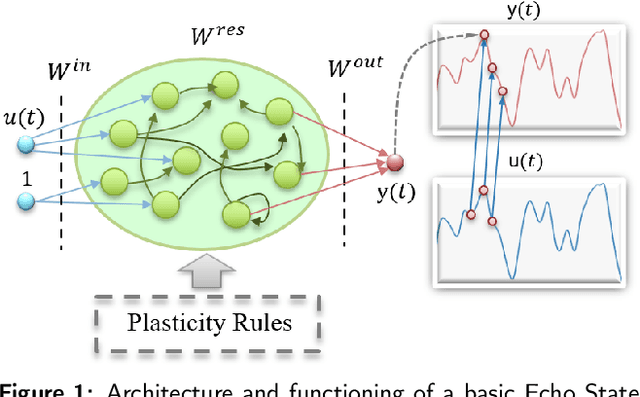
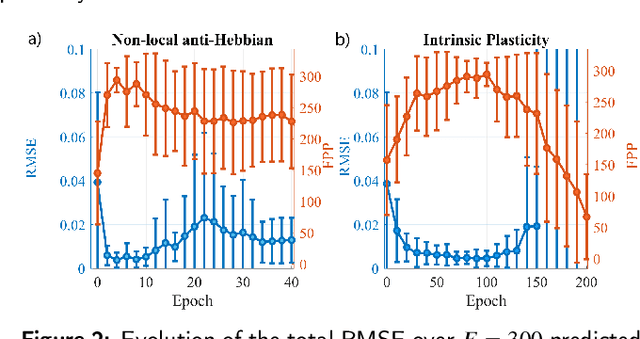
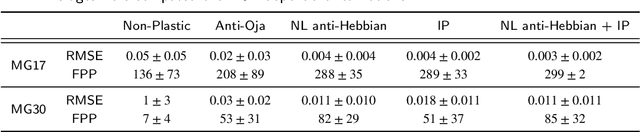
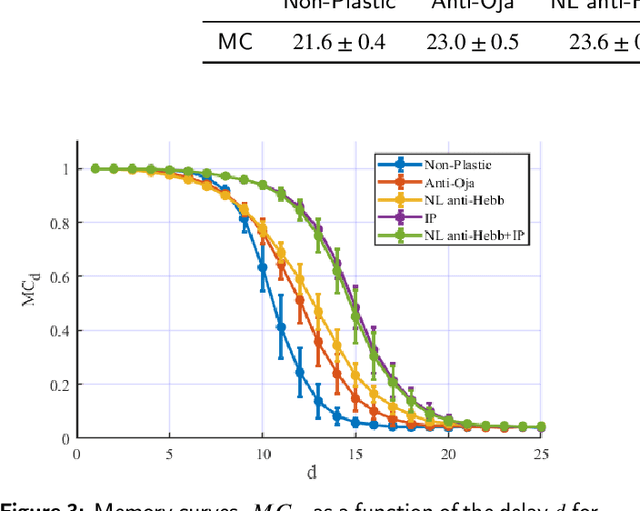
Reservoir Computing (RC) is an appealing approach in Machine Learning that combines the high computational capabilities of Recurrent Neural Networks with a fast and easy training method. Likewise, successful implementation of neuro-inspired plasticity rules into RC artificial networks has boosted the performance of the original models. In this manuscript, we analyze the role that plasticity rules play on the changes that lead to a better performance of RC. To this end, we implement synaptic and non-synaptic plasticity rules in a paradigmatic example of RC model: the Echo State Network. Testing on nonlinear time series prediction tasks, we show evidence that improved performance in all plastic models are linked to a decrease of the pair-wise correlations in the reservoir, as well as a significant increase of individual neurons ability to separate similar inputs in their activity space. Here we provide new insights on this observed improvement through the study of different stages on the plastic learning. From the perspective of the reservoir dynamics, optimal performance is found to occur close to the so-called edge of instability. Our results also show that it is possible to combine different forms of plasticity (namely synaptic and non-synaptic rules) to further improve the performance on prediction tasks, obtaining better results than those achieved with single-plasticity models.

Machine learning applied to quantum synchronization-assisted probing

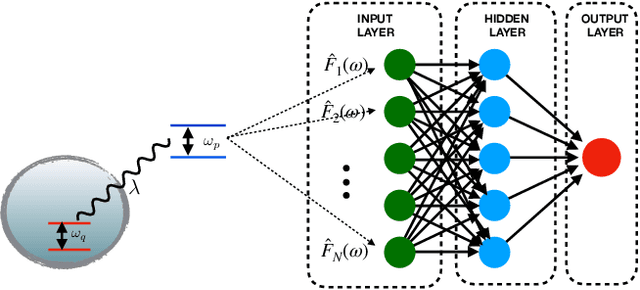
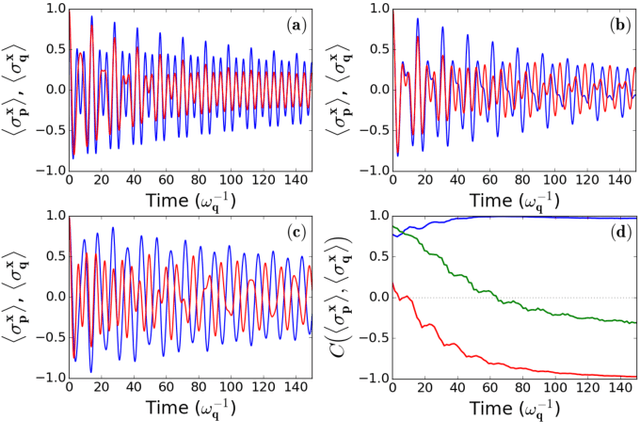
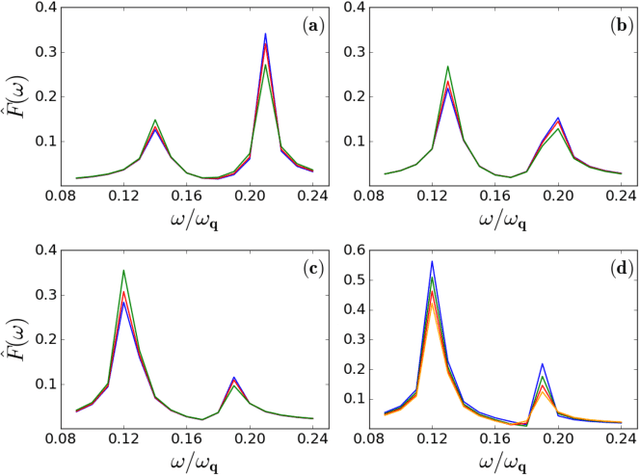
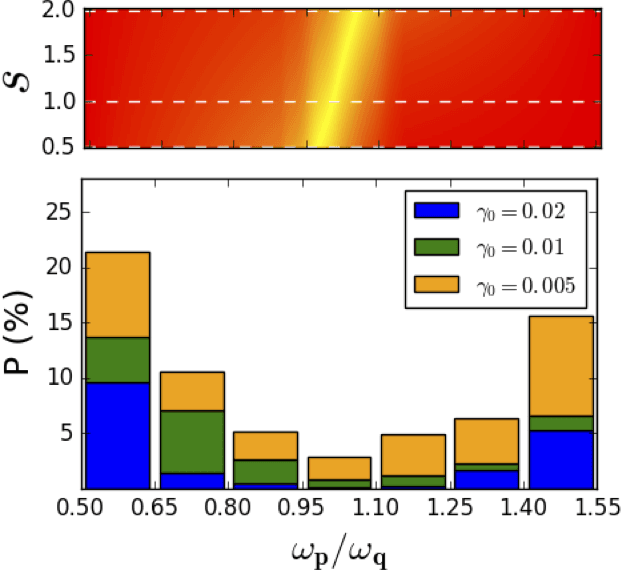
A probing scheme is considered with an accessible and controllable qubit, used to probe an out-of equilibrium system consisting of a second qubit interacting with an environment. Quantum spontaneous synchronization between the probe and the system emerges in this model and, by tuning the probe frequency, can occur both in-phase and in anti-phase. We analyze the capability of machine learning in this probing scheme based on quantum synchronization. An artificial neural network is used to infer, from a probe observable, main dissipation features, such as the environment Ohmicity index. The efficiency of the algorithm in the presence of some noise in the dataset is also considered. We show that the performance in either classification and regression is significantly improved due to the in/anti-phase synchronization transition. This opens the way to the characterization of environments with arbitrary spectral densities.