Kaloyan Danovski
Dynamical stability and chaos in artificial neural network trajectories along training
Apr 08, 2024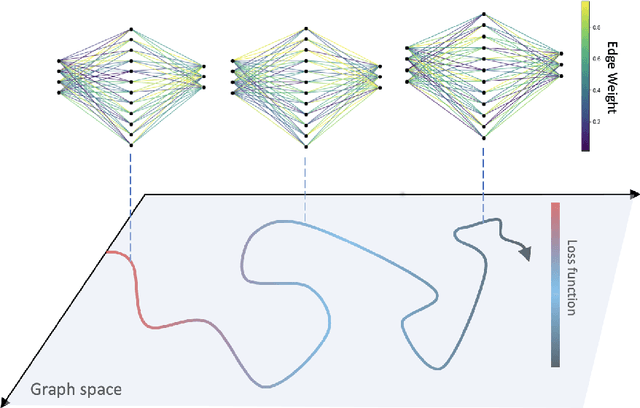
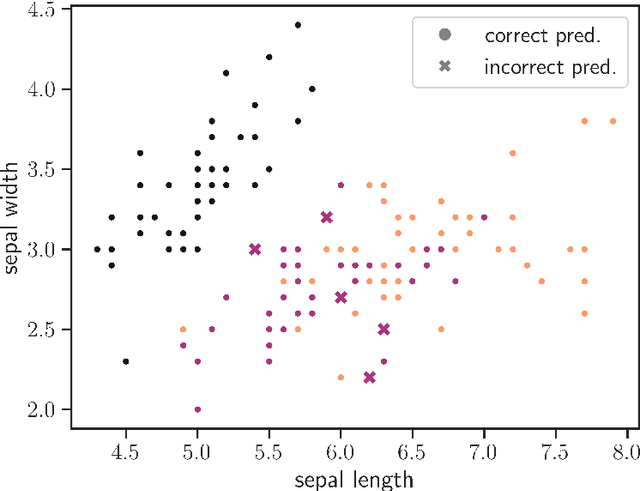
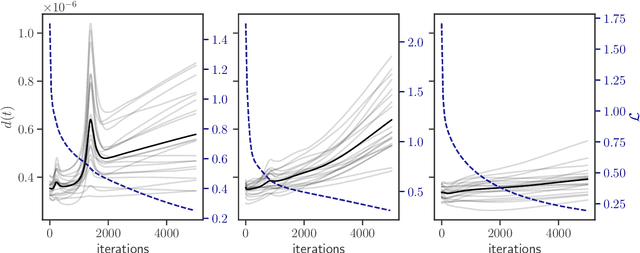
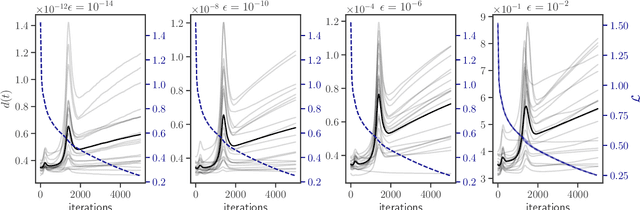
Abstract:The process of training an artificial neural network involves iteratively adapting its parameters so as to minimize the error of the network's prediction, when confronted with a learning task. This iterative change can be naturally interpreted as a trajectory in network space -- a time series of networks -- and thus the training algorithm (e.g. gradient descent optimization of a suitable loss function) can be interpreted as a dynamical system in graph space. In order to illustrate this interpretation, here we study the dynamical properties of this process by analyzing through this lens the network trajectories of a shallow neural network, and its evolution through learning a simple classification task. We systematically consider different ranges of the learning rate and explore both the dynamical and orbital stability of the resulting network trajectories, finding hints of regular and chaotic behavior depending on the learning rate regime. Our findings are put in contrast to common wisdom on convergence properties of neural networks and dynamical systems theory. This work also contributes to the cross-fertilization of ideas between dynamical systems theory, network theory and machine learning
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge