Adaptive control of recurrent neural networks using conceptors

Recurrent Neural Networks excel at predicting and generating complex high-dimensional temporal patterns. Due to their inherent nonlinear dynamics and memory, they can learn unbounded temporal dependencies from data. In a Machine Learning setting, the network's parameters are adapted during a training phase to match the requirements of a given task/problem increasing its computational capabilities. After the training, the network parameters are kept fixed to exploit the learned computations. The static parameters thereby render the network unadaptive to changing conditions, such as external or internal perturbation. In this manuscript, we demonstrate how keeping parts of the network adaptive even after the training enhances its functionality and robustness. Here, we utilize the conceptor framework and conceptualize an adaptive control loop analyzing the network's behavior continuously and adjusting its time-varying internal representation to follow a desired target. We demonstrate how the added adaptivity of the network supports the computational functionality in three distinct tasks: interpolation of temporal patterns, stabilization against partial network degradation, and robustness against input distortion. Our results highlight the potential of adaptive networks in machine learning beyond training, enabling them to not only learn complex patterns but also dynamically adjust to changing environments, ultimately broadening their applicability.

Inferring untrained complex dynamics of delay systems using an adapted echo state network

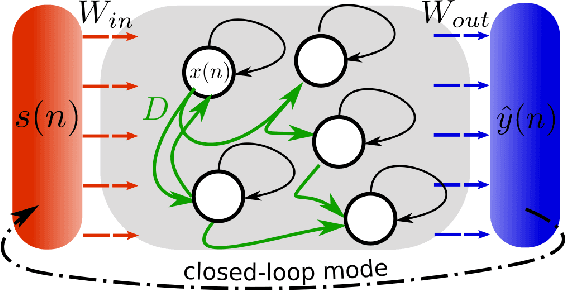
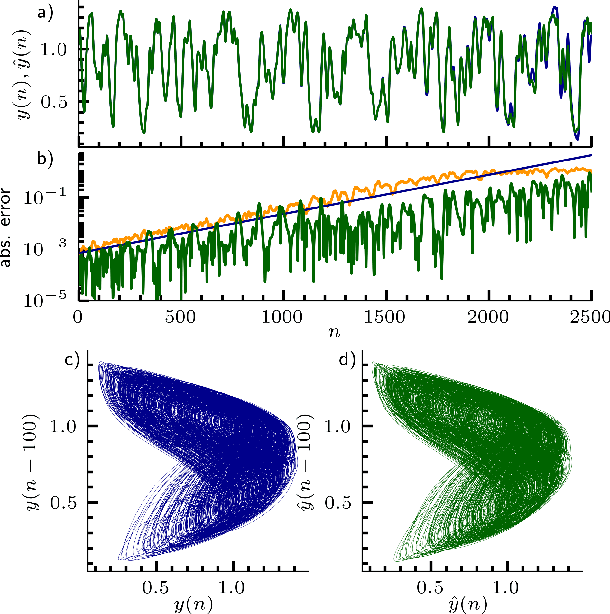
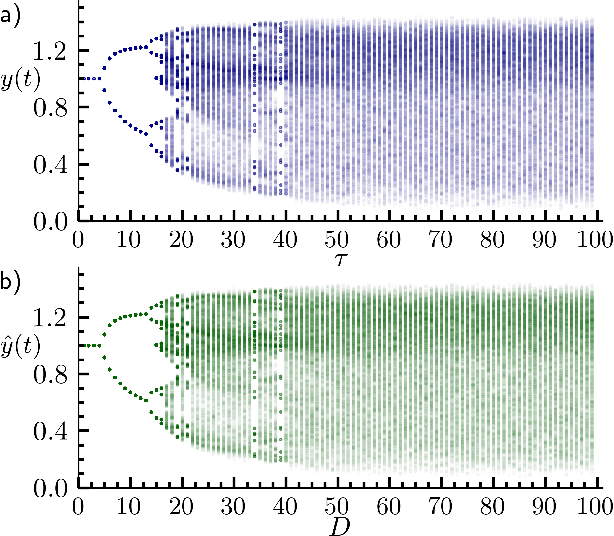
Caused by finite signal propagation velocities, many complex systems feature time delays that may induce high-dimensional chaotic behavior and make forecasting intricate. Here, we propose an echo state network adaptable to the physics of systems with arbitrary delays. After training the network to forecast a system with a unique and sufficiently long delay, it already learned to predict the system dynamics for all other delays. A simple adaptation of the network's topology allows us to infer untrained features such as high-dimensional chaotic attractors, bifurcations, and even multistabilities, that emerge with shorter and longer delays. Thus, the fusion of physical knowledge of the delay system and data-driven machine learning yields a model with high generalization capabilities and unprecedented prediction accuracy.

Deep Time-Delay Reservoir Computing: Dynamics and Memory Capacity

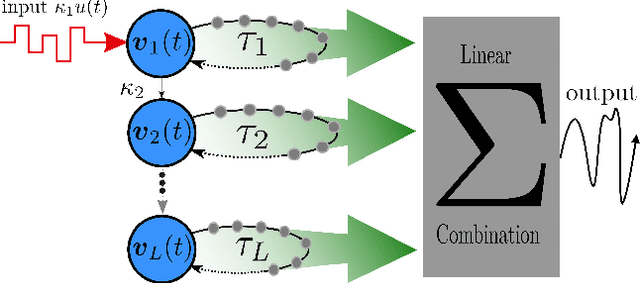
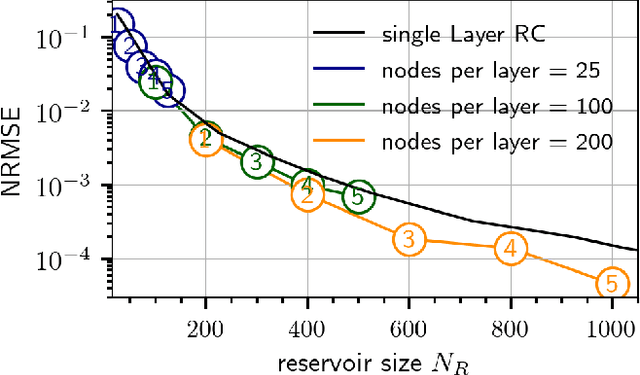
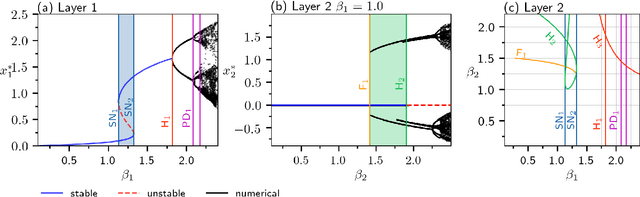
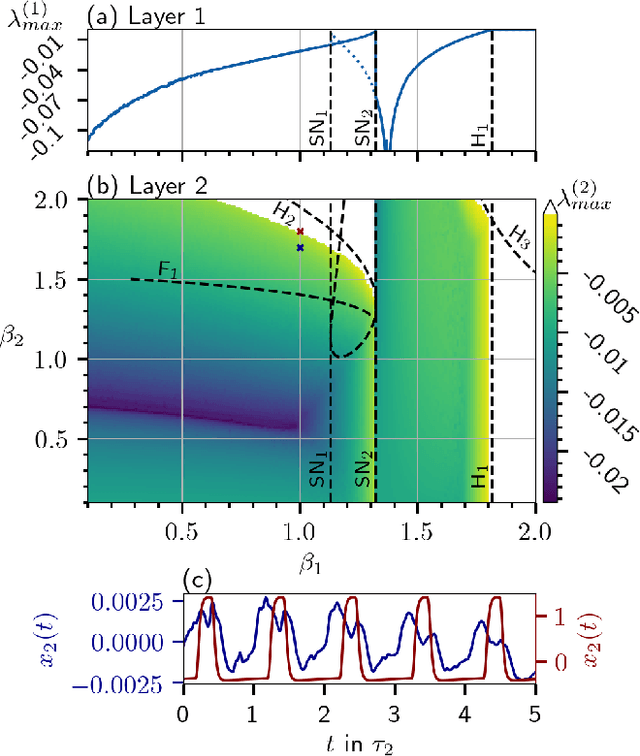
The Deep Time-Delay Reservoir Computing concept utilizes unidirectionally connected systems with time-delays for supervised learning. We present how the dynamical properties of a deep Ikeda-based reservoir are related to its memory capacity (MC) and how that can be used for optimization. In particular, we analyze bifurcations of the corresponding autonomous system and compute conditional Lyapunov exponents, which measure the generalized synchronization between the input and the layer dynamics. We show how the MC is related to the systems distance to bifurcations or magnitude of the conditional Lyapunov exponent. The interplay of different dynamical regimes leads to a adjustable distribution between linear and nonlinear MC. Furthermore, numerical simulations show resonances between clock cycle and delays of the layers in all degrees of the MC. Contrary to MC losses in a single-layer reservoirs, these resonances can boost separate degrees of the MC and can be used, e.g., to design a system with maximum linear MC. Accordingly, we present two configurations that empower either high nonlinear MC or long time linear MC.