Master memory function for delay-based reservoir computers with single-variable dynamics

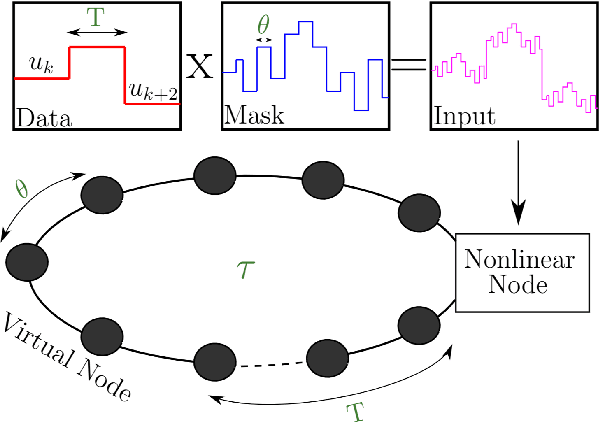
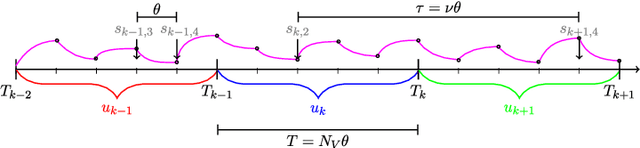
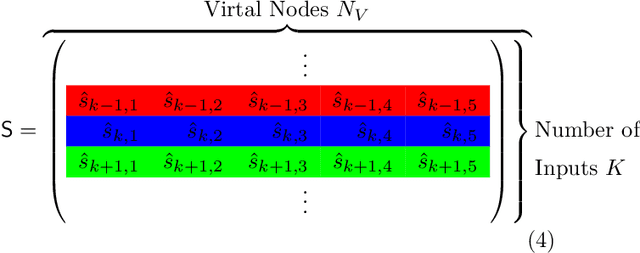
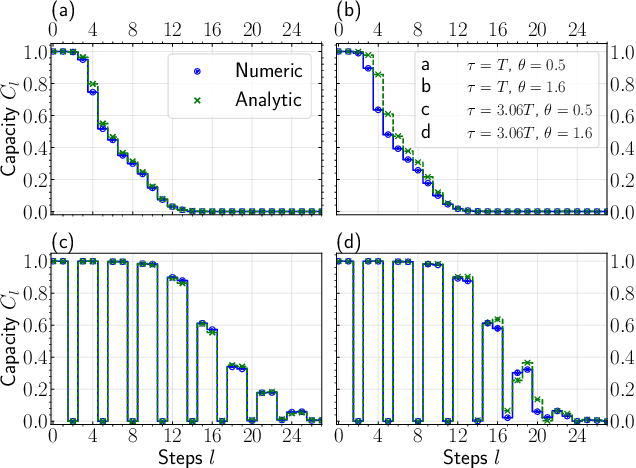
We show that many delay-based reservoir computers considered in the literature can be characterized by a universal master memory function (MMF). Once computed for two independent parameters, this function provides linear memory capacity for any delay-based single-variable reservoir with small inputs. Moreover, we propose an analytical description of the MMF that enables its efficient and fast computation. Our approach can be applied not only to reservoirs governed by known dynamical rules such as Mackey-Glass or Ikeda-like systems but also to reservoirs whose dynamical model is not available. We also present results comparing the performance of the reservoir computer and the memory capacity given by the MMF.

Infinite-dimensional Folded-in-time Deep Neural Networks

The method recently introduced in arXiv:2011.10115 realizes a deep neural network with just a single nonlinear element and delayed feedback. It is applicable for the description of physically implemented neural networks. In this work, we present an infinite-dimensional generalization, which allows for a more rigorous mathematical analysis and a higher flexibility in choosing the weight functions. Precisely speaking, the weights are described by Lebesgue integrable functions instead of step functions. We also provide a functional backpropagation algorithm, which enables gradient descent training of the weights. In addition, with a slight modification, our concept realizes recurrent neural networks.

Deep Learning with a Single Neuron: Folding a Deep Neural Network in Time using Feedback-Modulated Delay Loops

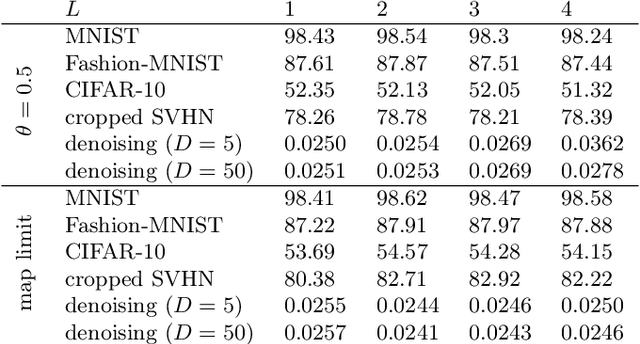
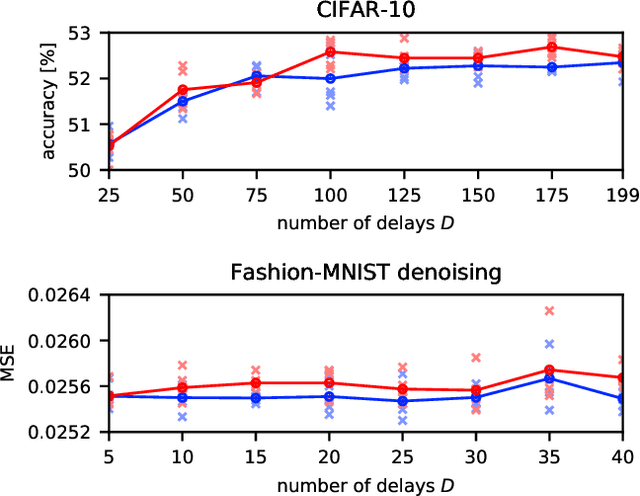
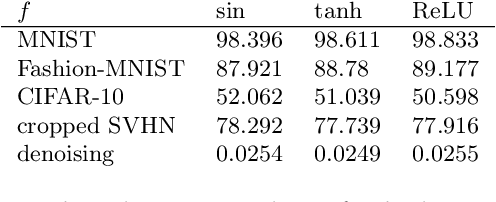
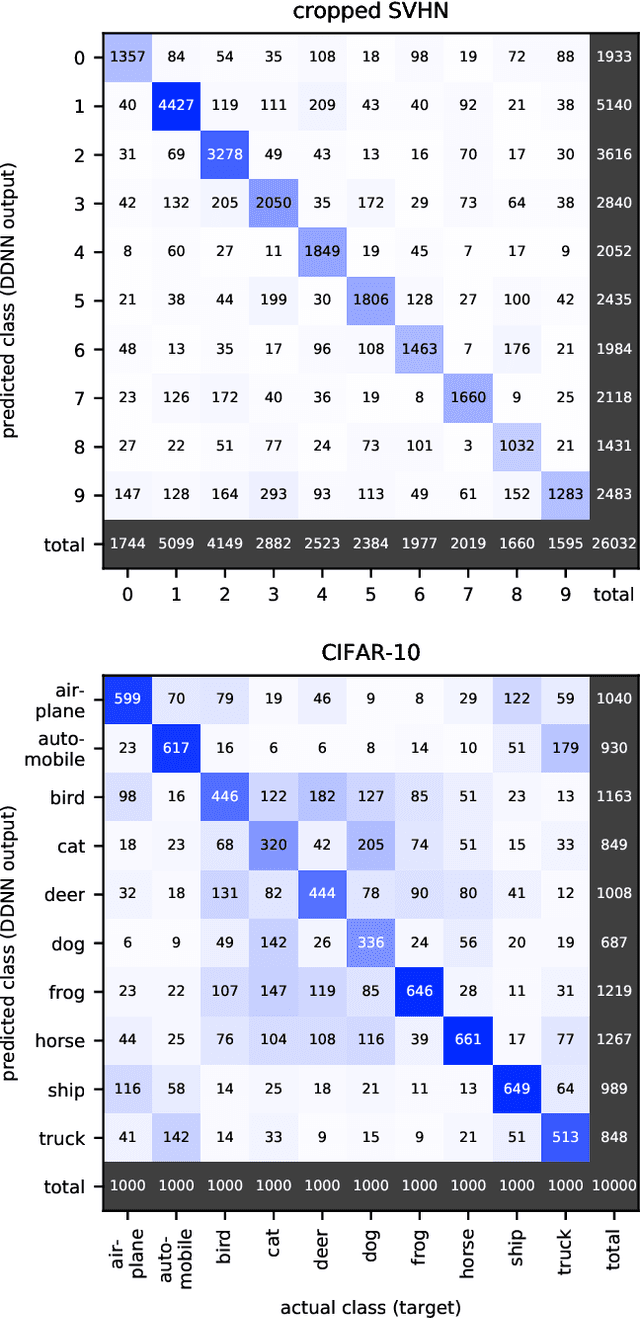
Deep neural networks are among the most widely applied machine learning tools showing outstanding performance in a broad range of tasks. We present a method for folding a deep neural network of arbitrary size into a single neuron with multiple time-delayed feedback loops. This single-neuron deep neural network comprises only a single nonlinearity and appropriately adjusted modulations of the feedback signals. The network states emerge in time as a temporal unfolding of the neuron's dynamics. By adjusting the feedback-modulation within the loops, we adapt the network's connection weights. These connection weights are determined via a modified back-propagation algorithm that we designed for such types of networks. Our approach fully recovers standard Deep Neural Networks (DNN), encompasses sparse DNNs, and extends the DNN concept toward dynamical systems implementations. The new method, which we call Folded-in-time DNN (Fit-DNN), exhibits promising performance in a set of benchmark tasks.

Improving Delay Based Reservoir Computing via Eigenvalue Analysis

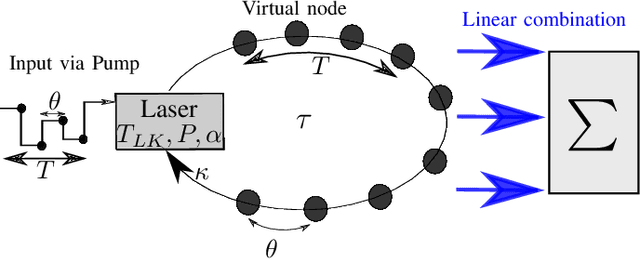
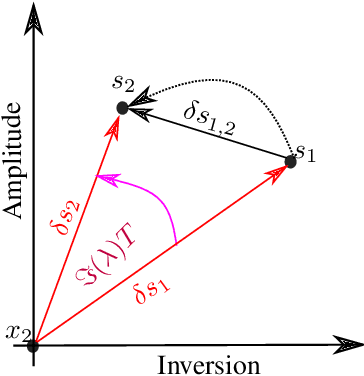
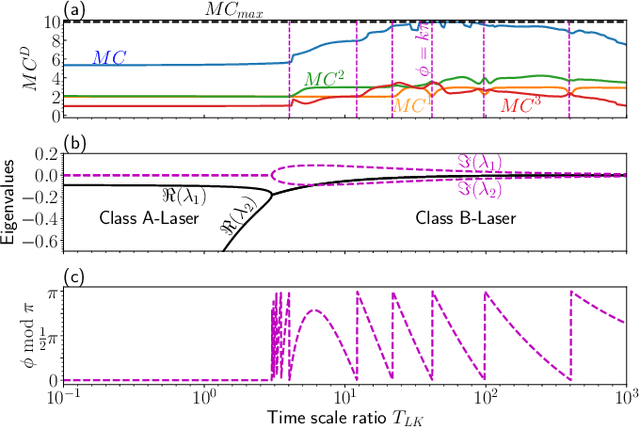
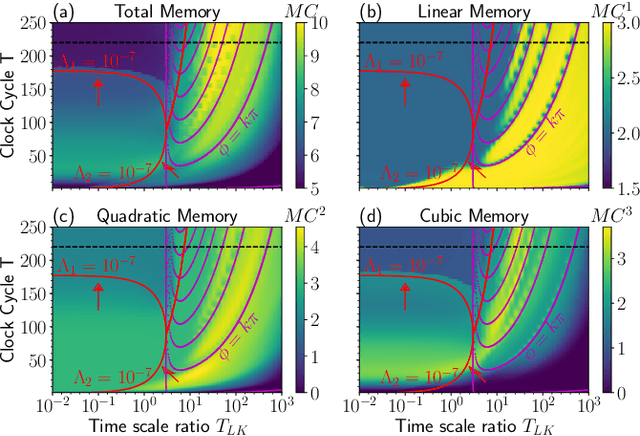
We analyze the reservoir computation capability of the Lang-Kobayashi system by comparing the numerically computed recall capabilities and the eigenvalue spectrum. We show that these two quantities are deeply connected, and thus the reservoir computing performance is predictable by analyzing the eigenvalue spectrum. Our results suggest that any dynamical system used as a reservoir can be analyzed in this way as long as the reservoir perturbations are sufficiently small. Optimal performance is found for a system with the eigenvalues having real parts close to zero and off-resonant imaginary parts.

Deep Time-Delay Reservoir Computing: Dynamics and Memory Capacity

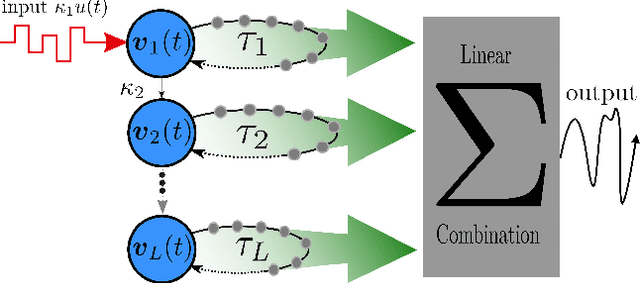
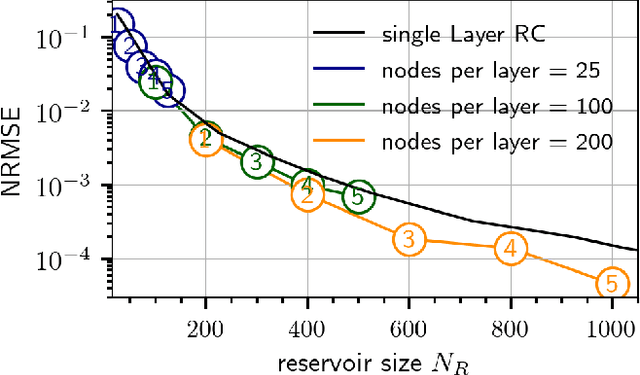
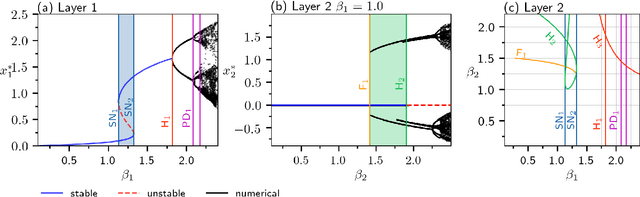
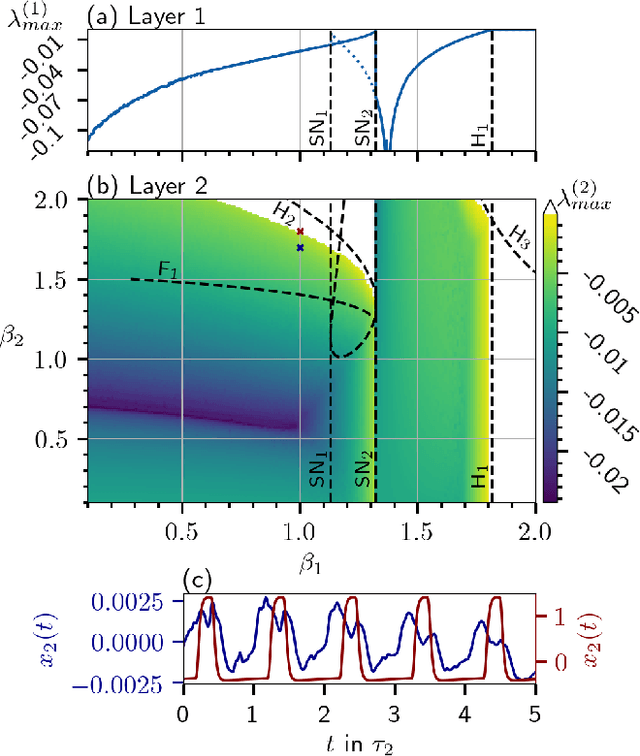
The Deep Time-Delay Reservoir Computing concept utilizes unidirectionally connected systems with time-delays for supervised learning. We present how the dynamical properties of a deep Ikeda-based reservoir are related to its memory capacity (MC) and how that can be used for optimization. In particular, we analyze bifurcations of the corresponding autonomous system and compute conditional Lyapunov exponents, which measure the generalized synchronization between the input and the layer dynamics. We show how the MC is related to the systems distance to bifurcations or magnitude of the conditional Lyapunov exponent. The interplay of different dynamical regimes leads to a adjustable distribution between linear and nonlinear MC. Furthermore, numerical simulations show resonances between clock cycle and delays of the layers in all degrees of the MC. Contrary to MC losses in a single-layer reservoirs, these resonances can boost separate degrees of the MC and can be used, e.g., to design a system with maximum linear MC. Accordingly, we present two configurations that empower either high nonlinear MC or long time linear MC.

Performance boost of time-delay reservoir computing by non-resonant clock cycle

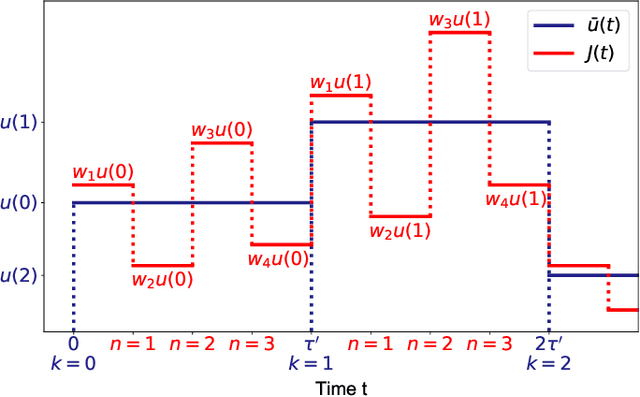
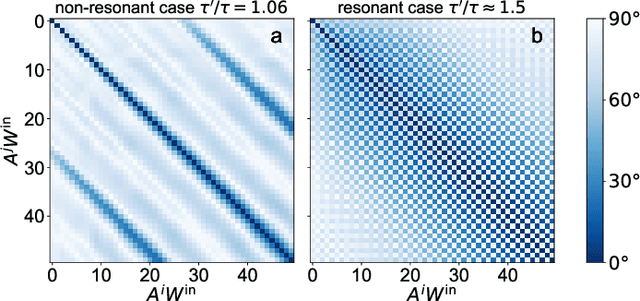
The time-delay-based reservoir computing setup has seen tremendous success in both experiment and simulation. It allows for the construction of large neuromorphic computing systems with only few components. However, until now the interplay of the different timescales has not been investigated thoroughly. In this manuscript, we investigate the effects of a mismatch between the time-delay and the clock cycle for a general model. Typically, these two time scales are considered to be equal. Here we show that the case of equal or rationally related time-delay and clock cycle could be actively detrimental and leads to an increase of the approximation error of the reservoir. In particular, we can show that non-resonant ratios of these time scales have maximal memory capacities. We achieve this by translating the periodically driven delay-dynamical system into an equivalent network. Networks that originate from a system with resonant delay-times and clock cycles fail to utilize all of their degrees of freedom, which causes the degradation of their performance.