Michiel Hermans
Random pattern and frequency generation using a photonic reservoir computer with output feedback
Dec 19, 2020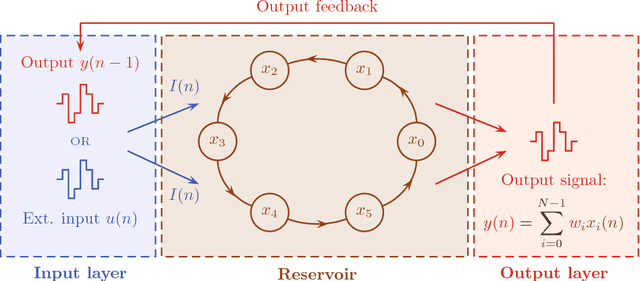
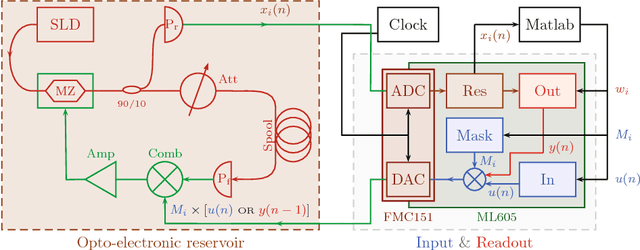
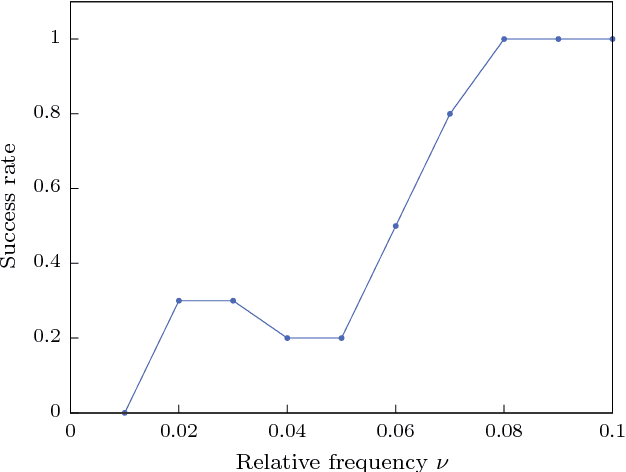
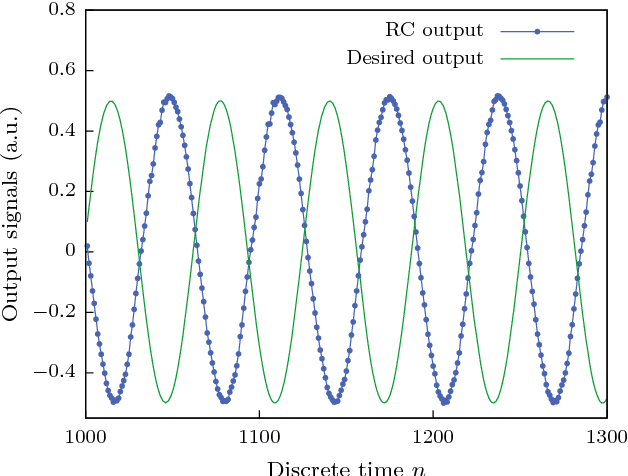
Abstract:Reservoir computing is a bio-inspired computing paradigm for processing time dependent signals. The performance of its analogue implementations matches other digital algorithms on a series of benchmark tasks. Their potential can be further increased by feeding the output signal back into the reservoir, which would allow to apply the algorithm to time series generation. This requires, in principle, implementing a sufficiently fast readout layer for real-time output computation. Here we achieve this with a digital output layer driven by a FPGA chip. We demonstrate the first opto-electronic reservoir computer with output feedback and test it on two examples of time series generation tasks: frequency and random pattern generation. We obtain very good results on the first task, similar to idealised numerical simulations. The performance on the second one, however, suffers from the experimental noise. We illustrate this point with a detailed investigation of the consequences of noise on the performance of a physical reservoir computer with output feedback. Our work thus opens new possible applications for analogue reservoir computing and brings new insights on the impact of noise on the output feedback.
* 15 pages, 9 figures. arXiv admin note: substantial text overlap with arXiv:1802.02026
A Differentiable Physics Engine for Deep Learning in Robotics
Nov 24, 2018
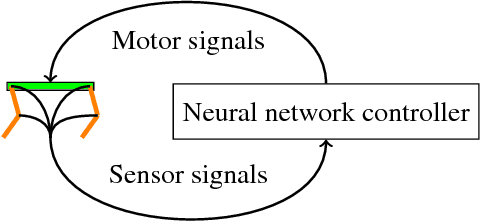
Abstract:An important field in robotics is the optimization of controllers. Currently, robots are often treated as a black box in this optimization process, which is the reason why derivative-free optimization methods such as evolutionary algorithms or reinforcement learning are omnipresent. When gradient-based methods are used, models are kept small or rely on finite difference approximations for the Jacobian. This method quickly grows expensive with increasing numbers of parameters, such as found in deep learning. We propose the implementation of a modern physics engine, which can differentiate control parameters. This engine is implemented for both CPU and GPU. Firstly, this paper shows how such an engine speeds up the optimization process, even for small problems. Furthermore, it explains why this is an alternative approach to deep Q-learning, for using deep learning in robotics. Finally, we argue that this is a big step for deep learning in robotics, as it opens up new possibilities to optimize robots, both in hardware and software.
Embodiment of Learning in Electro-Optical Signal Processors
Oct 27, 2016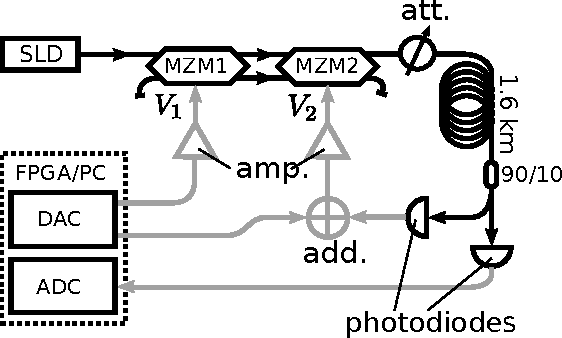
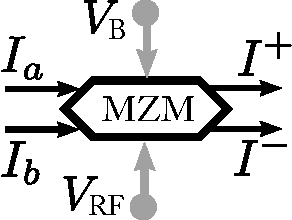
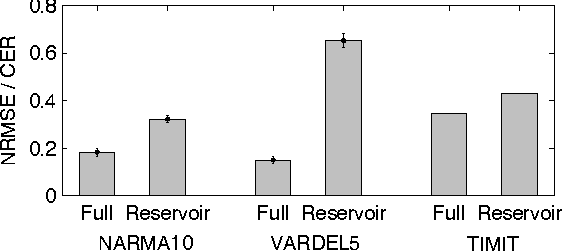
Abstract:Delay-coupled electro-optical systems have received much attention for their dynamical properties and their potential use in signal processing. In particular it has recently been demonstrated, using the artificial intelligence algorithm known as reservoir computing, that photonic implementations of such systems solve complex tasks such as speech recognition. Here we show how the backpropagation algorithm can be physically implemented on the same electro-optical delay-coupled architecture used for computation with only minor changes to the original design. We find that, compared when the backpropagation algorithm is not used, the error rate of the resulting computing device, evaluated on three benchmark tasks, decreases considerably. This demonstrates that electro-optical analog computers can embody a large part of their own training process, allowing them to be applied to new, more difficult tasks.
* Main text (5 pages, 2 figures) merged with the supplementary material (8 pages, 5 figures)
Online Training of an Opto-Electronic Reservoir Computer Applied to Real-Time Channel Equalisation
Oct 20, 2016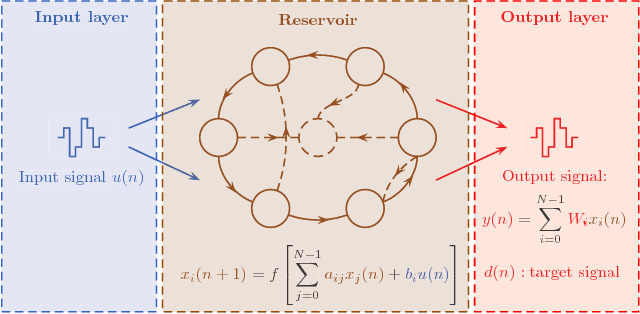
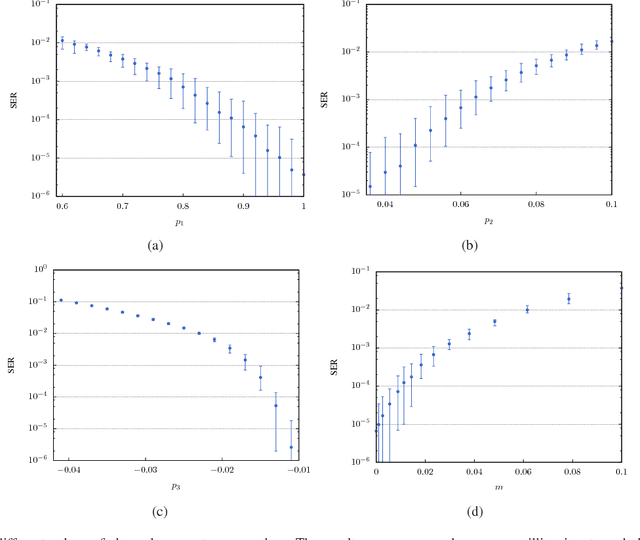
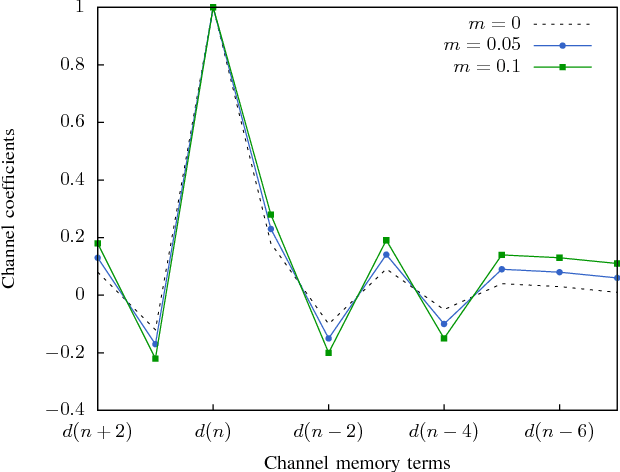
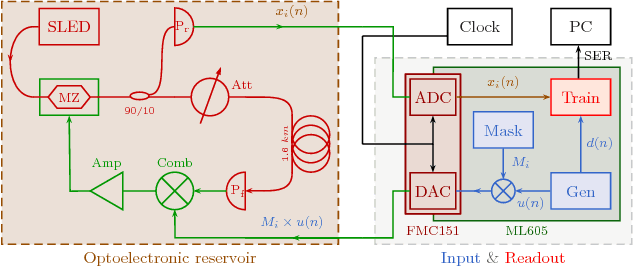
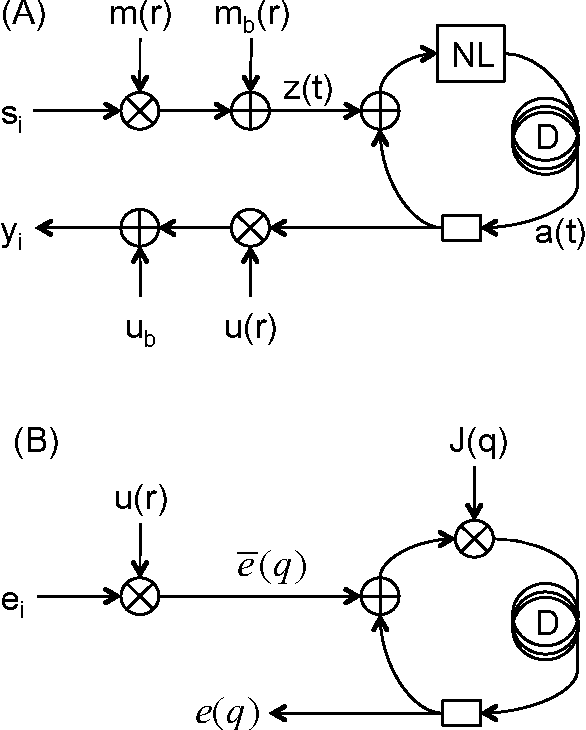
Abstract:Reservoir Computing is a bio-inspired computing paradigm for processing time dependent signals. The performance of its analogue implementation are comparable to other state of the art algorithms for tasks such as speech recognition or chaotic time series prediction, but these are often constrained by the offline training methods commonly employed. Here we investigated the online learning approach by training an opto-electronic reservoir computer using a simple gradient descent algorithm, programmed on an FPGA chip. Our system was applied to wireless communications, a quickly growing domain with an increasing demand for fast analogue devices to equalise the nonlinear distorted channels. We report error rates up to two orders of magnitude lower than previous implementations on this task. We show that our system is particularly well-suited for realistic channel equalisation by testing it on a drifting and a switching channels and obtaining good performances
* 13 pages, 10 figures
Towards Trainable Media: Using Waves for Neural Network-Style Training
Sep 30, 2015



Abstract:In this paper we study the concept of using the interaction between waves and a trainable medium in order to construct a matrix-vector multiplier. In particular we study such a device in the context of the backpropagation algorithm, which is commonly used for training neural networks. Here, the weights of the connections between neurons are trained by multiplying a `forward' signal with a backwards propagating `error' signal. We show that this concept can be extended to trainable media, where the gradient for the local wave number is given by multiplying signal waves and error waves. We provide a numerical example of such a system with waves traveling freely in a trainable medium, and we discuss a potential way to build such a device in an integrated photonics chip.
Photonic Delay Systems as Machine Learning Implementations
Jan 12, 2015



Abstract:Nonlinear photonic delay systems present interesting implementation platforms for machine learning models. They can be extremely fast, offer great degrees of parallelism and potentially consume far less power than digital processors. So far they have been successfully employed for signal processing using the Reservoir Computing paradigm. In this paper we show that their range of applicability can be greatly extended if we use gradient descent with backpropagation through time on a model of the system to optimize the input encoding of such systems. We perform physical experiments that demonstrate that the obtained input encodings work well in reality, and we show that optimized systems perform significantly better than the common Reservoir Computing approach. The results presented here demonstrate that common gradient descent techniques from machine learning may well be applicable on physical neuro-inspired analog computers.
Trainable and Dynamic Computing: Error Backpropagation through Physical Media
Jul 24, 2014



Abstract:Machine learning algorithms, and more in particular neural networks, arguably experience a revolution in terms of performance. Currently, the best systems we have for speech recognition, computer vision and similar problems are based on neural networks, trained using the half-century old backpropagation algorithm. Despite the fact that neural networks are a form of analog computers, they are still implemented digitally for reasons of convenience and availability. In this paper we demonstrate how we can design physical linear dynamic systems with non-linear feedback as a generic platform for dynamic, neuro-inspired analog computing. We show that a crucial advantage of this setup is that the error backpropagation can be performed physically as well, which greatly speeds up the optimisation process. As we show in this paper, using one experimentally validated and one conceptual example, such systems may be the key to providing a relatively straightforward mechanism for constructing highly scalable, fully dynamic analog computers.
Memristor models for machine learning
Jul 14, 2014Abstract:In the quest for alternatives to traditional CMOS, it is being suggested that digital computing efficiency and power can be improved by matching the precision to the application. Many applications do not need the high precision that is being used today. In particular, large gains in area- and power efficiency could be achieved by dedicated analog realizations of approximate computing engines. In this work, we explore the use of memristor networks for analog approximate computation, based on a machine learning framework called reservoir computing. Most experimental investigations on the dynamics of memristors focus on their nonvolatile behavior. Hence, the volatility that is present in the developed technologies is usually unwanted and it is not included in simulation models. In contrast, in reservoir computing, volatility is not only desirable but necessary. Therefore, in this work, we propose two different ways to incorporate it into memristor simulation models. The first is an extension of Strukov's model and the second is an equivalent Wiener model approximation. We analyze and compare the dynamical properties of these models and discuss their implications for the memory and the nonlinear processing capacity of memristor networks. Our results indicate that device variability, increasingly causing problems in traditional computer design, is an asset in the context of reservoir computing. We conclude that, although both models could lead to useful memristor based reservoir computing systems, their computational performance will differ. Therefore, experimental modeling research is required for the development of accurate volatile memristor models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge