ChronoFormer: Time-Aware Transformer Architectures for Structured Clinical Event Modeling

The temporal complexity of electronic health record (EHR) data presents significant challenges for predicting clinical outcomes using machine learning. This paper proposes ChronoFormer, an innovative transformer based architecture specifically designed to encode and leverage temporal dependencies in longitudinal patient data. ChronoFormer integrates temporal embeddings, hierarchical attention mechanisms, and domain specific masking techniques. Extensive experiments conducted on three benchmark tasks mortality prediction, readmission prediction, and long term comorbidity onset demonstrate substantial improvements over current state of the art methods. Furthermore, detailed analyses of attention patterns underscore ChronoFormer's capability to capture clinically meaningful long range temporal relationships.

Exploring Neural Ordinary Differential Equations as Interpretable Healthcare classifiers

Deep Learning has emerged as one of the most significant innovations in machine learning. However, a notable limitation of this field lies in the ``black box" decision-making processes, which have led to skepticism within groups like healthcare and scientific communities regarding its applicability. In response, this study introduces a interpretable approach using Neural Ordinary Differential Equations (NODEs), a category of neural network models that exploit the dynamics of differential equations for representation learning. Leveraging their foundation in differential equations, we illustrate the capability of these models to continuously process textual data, marking the first such model of its kind, and thereby proposing a promising direction for future research in this domain. The primary objective of this research is to propose a novel architecture for groups like healthcare that require the predictive capabilities of deep learning while emphasizing the importance of model transparency demonstrated in NODEs.

Advanced Equalization in 112 Gb/s Upstream PON Using a Novel Fourier Convolution-based Network

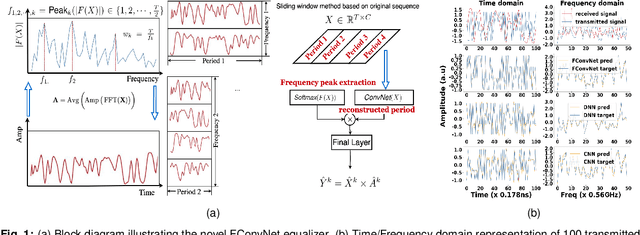
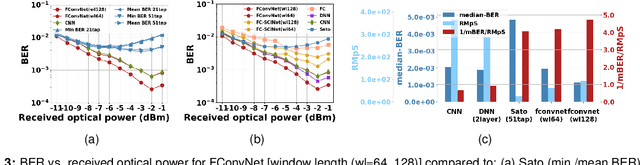
We experimentally demonstrate a novel, low-complexity Fourier Convolution-based Network (FConvNet) based equalizer for 112 Gb/s upstream PAM4-PON. At a BER of 0.005, FConvNet enhances the receiver sensitivity by 2 and 1 dB compared to a 51-tap Sato equalizer and benchmark machine learning algorithms respectively.

Machine Learning in Short-Reach Optical Systems: A Comprehensive Survey

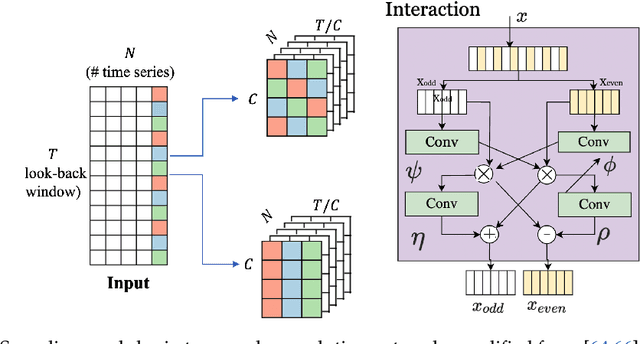
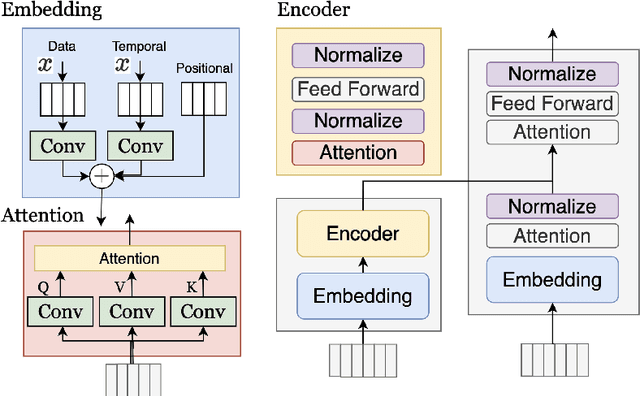
In recent years, extensive research has been conducted to explore the utilization of machine learning algorithms in various direct-detected and self-coherent short-reach communication applications. These applications encompass a wide range of tasks, including bandwidth request prediction, signal quality monitoring, fault detection, traffic prediction, and digital signal processing (DSP)-based equalization. As a versatile approach, machine learning demonstrates the ability to address stochastic phenomena in optical systems networks where deterministic methods may fall short. However, when it comes to DSP equalization algorithms, their performance improvements are often marginal, and their complexity is prohibitively high, especially in cost-sensitive short-reach communications scenarios such as passive optical networks (PONs). They excel in capturing temporal dependencies, handling irregular or nonlinear patterns effectively, and accommodating variable time intervals. Within this extensive survey, we outline the application of machine learning techniques in short-reach communications, specifically emphasizing their utilization in high-bandwidth demanding PONs. Notably, we introduce a novel taxonomy for time-series methods employed in machine learning signal processing, providing a structured classification framework. Our taxonomy categorizes current time series methods into four distinct groups: traditional methods, Fourier convolution-based methods, transformer-based models, and time-series convolutional networks. Finally, we highlight prospective research directions within this rapidly evolving field and outline specific solutions to mitigate the complexity associated with hardware implementations. We aim to pave the way for more practical and efficient deployment of machine learning approaches in short-reach optical communication systems by addressing complexity concerns.

A Novel Machine Learning-based Equalizer for a Downstream 100G PAM-4 PON

A frequency-calibrated SCINet (FC-SCINet) equalizer is proposed for down-stream 100G PON with 28.7 dB path loss. At 5 km, FC-SCINet improves the BER by 88.87% compared to FFE and a 3-layer DNN with 10.57% lower complexity.

KIGLIS: Smart Networks for Smart Cities

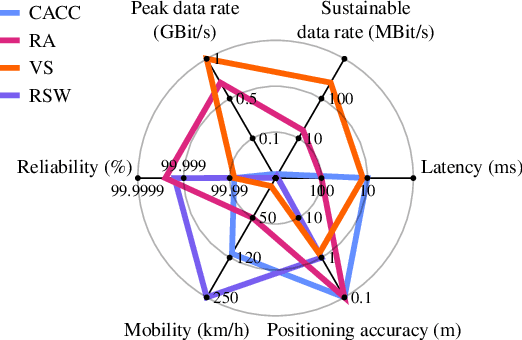
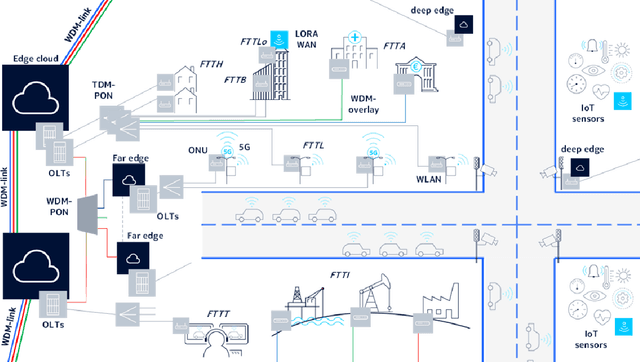
Smart cities will be characterized by a variety of intelligent and networked services, each with specific requirements for the underlying network infrastructure. While smart city architectures and services have been studied extensively, little attention has been paid to the network technology. The KIGLIS research project, consisting of a consortium of companies, universities and research institutions, focuses on artificial intelligence for optimizing fiber-optic networks of a smart city, with a special focus on future mobility applications, such as automated driving. In this paper, we present early results on our process of collecting smart city requirements for communication networks, which will lead towards reference infrastructure and architecture solutions. Finally, we suggest directions in which artificial intelligence will improve smart city networks.

56 GBaud PAM-4 100 km Transmission System with Photonic Processing Schemes

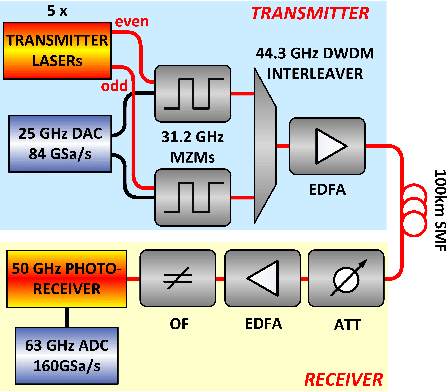
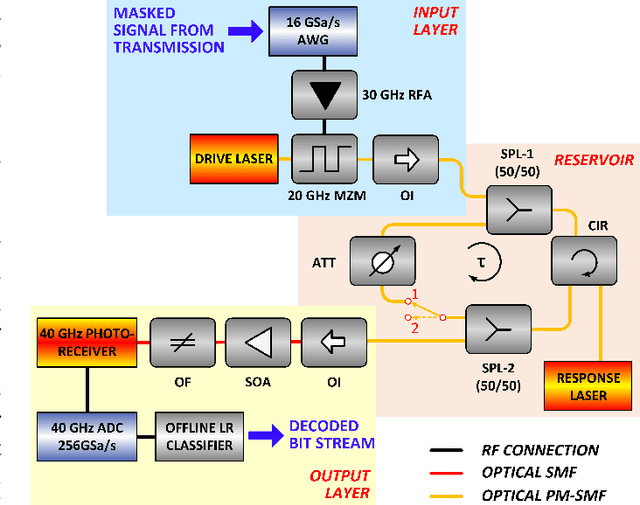
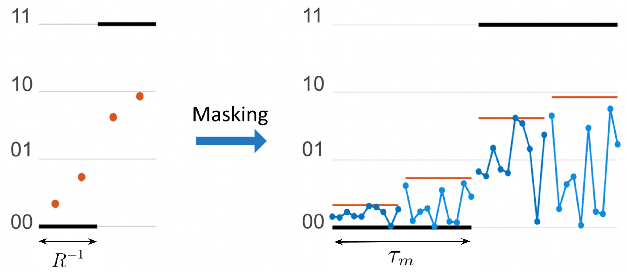
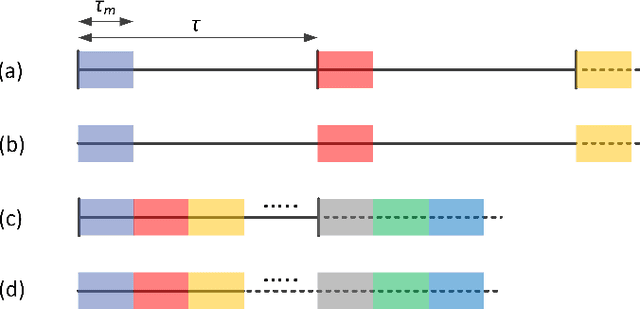
Analog photonic computing has been proposed and tested in recent years as an alternative approach for data recovery in fiber transmission systems. Photonic reservoir computing, performing nonlinear transformations of the transmitted signals and exhibiting internal fading memory, has been found advantageous for this kind of processing. In this work, we show that the effectiveness of the internal fading memory depends significantly on the properties of the signal to be processed. Specifically, we demonstrate two experimental photonic post-processing schemes for a 56 GBaud PAM-4 experimental transmission system, with 100 km uncompensated standard single-mode fiber and direct detection. We show that, for transmission systems with significant chromatic dispersion, the contribution of a photonic reservoir's fading memory to the computational performance is limited. In a comparison between the data recovery performances between a reservoir computing and an extreme learning machine fiber-based configuration, we find that both offer equivalent data recovery. The extreme learning machine approach eliminates the necessity of external recurrent connectivity, which simplifies the system and increases the computation speed. Error-free data recovery is experimentally demonstrated for an optical signal to noise ratio above 30 dB, outperforming an implementation of a Kramers-Kronig receiver in the digital domain.

Robust High Dimensional Expectation Maximization Algorithm via Trimmed Hard Thresholding

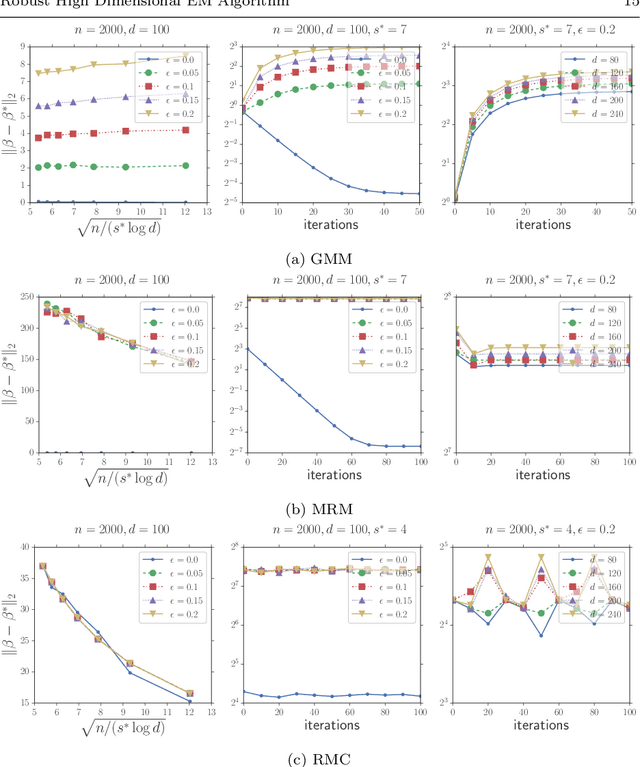
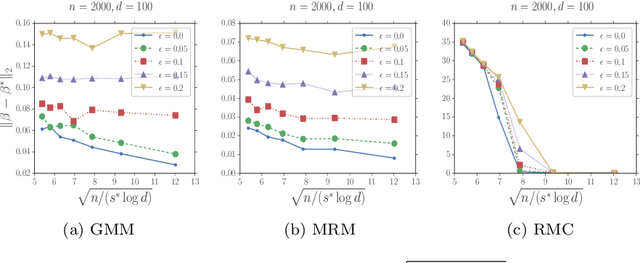
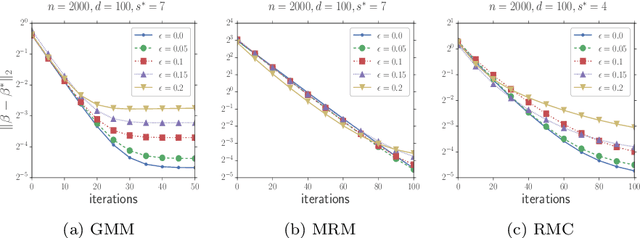
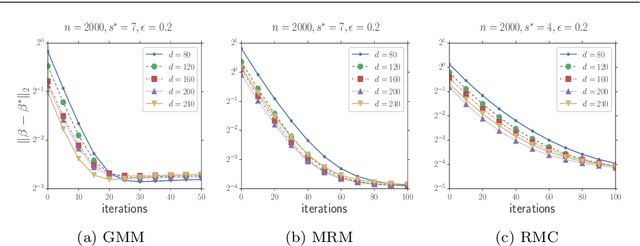
In this paper, we study the problem of estimating latent variable models with arbitrarily corrupted samples in high dimensional space ({\em i.e.,} $d\gg n$) where the underlying parameter is assumed to be sparse. Specifically, we propose a method called Trimmed (Gradient) Expectation Maximization which adds a trimming gradients step and a hard thresholding step to the Expectation step (E-step) and the Maximization step (M-step), respectively. We show that under some mild assumptions and with an appropriate initialization, the algorithm is corruption-proofing and converges to the (near) optimal statistical rate geometrically when the fraction of the corrupted samples $\epsilon$ is bounded by $ \tilde{O}(\frac{1}{\sqrt{n}})$. Moreover, we apply our general framework to three canonical models: mixture of Gaussians, mixture of regressions and linear regression with missing covariates. Our theory is supported by thorough numerical results.

Estimating Stochastic Linear Combination of Non-linear Regressions Efficiently and Scalably

Recently, many machine learning and statistical models such as non-linear regressions, the Single Index, Multi-index, Varying Coefficient Index Models and Two-layer Neural Networks can be reduced to or be seen as a special case of a new model which is called the \textit{Stochastic Linear Combination of Non-linear Regressions} model. However, due to the high non-convexity of the problem, there is no previous work study how to estimate the model. In this paper, we provide the first study on how to estimate the model efficiently and scalably. Specifically, we first show that with some mild assumptions, if the variate vector $x$ is multivariate Gaussian, then there is an algorithm whose output vectors have $\ell_2$-norm estimation errors of $O(\sqrt{\frac{p}{n}})$ with high probability, where $p$ is the dimension of $x$ and $n$ is the number of samples. The key idea of the proof is based on an observation motived by the Stein's lemma. Then we extend our result to the case where $x$ is bounded and sub-Gaussian using the zero-bias transformation, which could be seen as a generalization of the classic Stein's lemma. We also show that with some additional assumptions there is an algorithm whose output vectors have $\ell_\infty$-norm estimation errors of $O(\frac{1}{\sqrt{p}}+\sqrt{\frac{p}{n}})$ with high probability. We also provide a concrete example to show that there exists some link function which satisfies the previous assumptions. Finally, for both Gaussian and sub-Gaussian cases we propose a faster sub-sampling based algorithm and show that when the sub-sample sizes are large enough then the estimation errors will not be sacrificed by too much. Experiments for both cases support our theoretical results. To the best of our knowledge, this is the first work that studies and provides theoretical guarantees for the stochastic linear combination of non-linear regressions model.

Consistent $k$-Median: Simpler, Better and Robust

In this paper we introduce and study the online consistent $k$-clustering with outliers problem, generalizing the non-outlier version of the problem studied in [Lattanzi-Vassilvitskii, ICML17]. We show that a simple local-search based online algorithm can give a bicriteria constant approximation for the problem with $O(k^2 \log^2 (nD))$ swaps of medians (recourse) in total, where $D$ is the diameter of the metric. When restricted to the problem without outliers, our algorithm is simpler, deterministic and gives better approximation ratio and recourse, compared to that of [Lattanzi-Vassilvitskii, ICML17].