Robust High Dimensional Expectation Maximization Algorithm via Trimmed Hard Thresholding
Paper and Code
Oct 19, 2020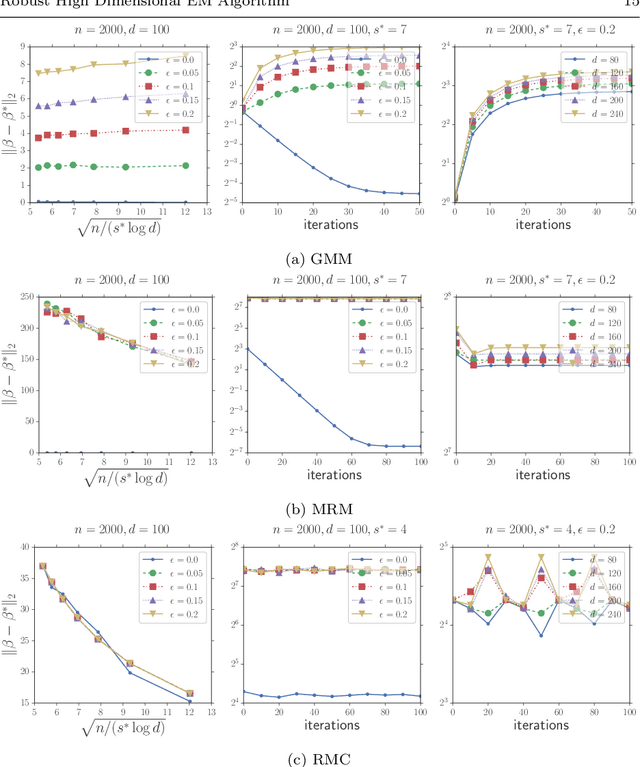
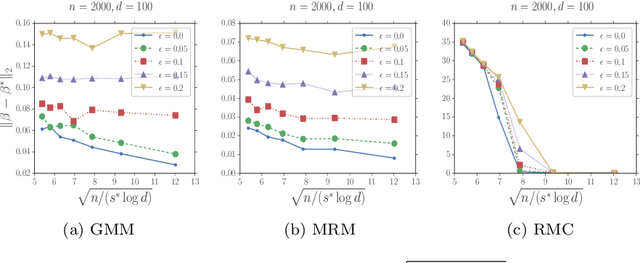
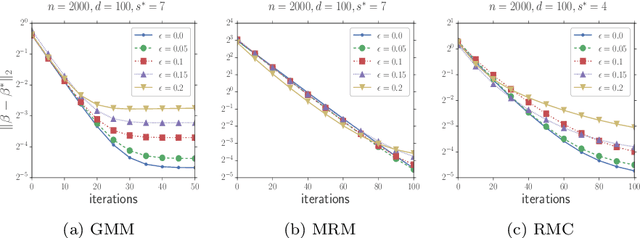
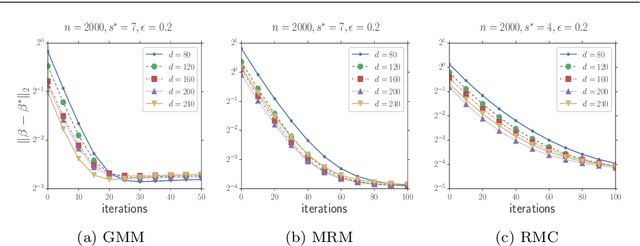
In this paper, we study the problem of estimating latent variable models with arbitrarily corrupted samples in high dimensional space ({\em i.e.,} $d\gg n$) where the underlying parameter is assumed to be sparse. Specifically, we propose a method called Trimmed (Gradient) Expectation Maximization which adds a trimming gradients step and a hard thresholding step to the Expectation step (E-step) and the Maximization step (M-step), respectively. We show that under some mild assumptions and with an appropriate initialization, the algorithm is corruption-proofing and converges to the (near) optimal statistical rate geometrically when the fraction of the corrupted samples $\epsilon$ is bounded by $ \tilde{O}(\frac{1}{\sqrt{n}})$. Moreover, we apply our general framework to three canonical models: mixture of Gaussians, mixture of regressions and linear regression with missing covariates. Our theory is supported by thorough numerical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge